T r i g o n o m e t r í a

Identidades trigonométricas fundamentales

En matemáticas, las identidades trigo­nométricas son igualdades que involucren razones trigonométricas, verificables para cualquier valor permisible de la variable o variables que se considere. Estas identidades son útiles siempre que se precise simplificar expresiones que inclu­yen razones trigonométricas.

TIPOS DE IDENTIDADES

Identidades por cociente

tane = senG cose

cotO: cose sen 0

Identidades recíprocas

C S C 6 = sen6

->senecsc6 = l

Identidades pitagóricas

sen 2 6 + cos 2 e = l

• sen 2 e=l-cos 2 6

cos 2 9=l-sen 2 e

l+tan 2 e=sec 2 e

• sec 2 6-tan 2 e=l

l+cot 2 e=csc 2 9

• csc 2 e-cot 2 e=i

Identidades auxiliares

• sen4G+cos 4e = 1 - 2sen2ecos29

• sen6G+cos6G = 1 - 3sen26cos29

• tanG+cote=sececsce

• sec 2 e+csc 2 e=sec 2ecsc 26

sec6 = 1 cose

->cos6sec6 =

cote = >tanecote = l tañe

Propiedad

Si asen6+ftcos9=c donde a2+b2=c2

entonces:

sen6 = — . cos8 = —

266

Semestral UNI T r i g o n o m e t r í a

Problemas resueltos 1. Demuestre que

Si asenx+f>cosx=c, además, a2+b2=c2

entonces se cumple que a b

senx = —, cosx = — c c

Demostración Del dato, tenemos que asenx+bcosx=c

-> asenx=c-ftcosx

Elevamos ambos miembros al cuadrado:

a 2 sen 2 x=c 2 - 2£>ccosx+¿>2cos2x

a 2 ( l - cosV) =c 2 - 2bccosx+b 2cos 2x

a2=c2+(a2+fc2)cos2x- 2í>ccosx

Al reemplazar a2=c2-b2 y a2+b2=c2

tenemos

c 2-í? 2=c 2+c 2cos 2x-2bccosx

c2cos2x-26ccosx-t-É>2=0

(ccosx-b) 2 =0 - » ccosx=b

b

Luego, cosx = —

Reemplazando el cosx en la igualdad asenx+£>cosx=c se tiene que

a c

\2/3

senx =

Si cotx = , encuentre el valor de

la siguiente expresión

a b ftsenx acosx

del primer cuadrante

, siendo x un arco

Resolución

Dato: cot x =

h 2 = { & 2 + { m 2

h2=íj+íb^h={í¿+íb*) 1/2

Luego

E = ¿isenx acosx fjyfa2 aHtí2

E = h\ + ¡ b a i

1 / 2 f aiía + bMb^

ab ,

N3/2

E =

UNI 95-1

ab

34b1 + 34a2

,3/2

x3/2

267

Semestral UNI • T r i g o n o m e t r í a

Identidades trigonométricas de arcos compuestos

IDENTIDADES PARA LA SUMA DE DOS ARCOS

sen(a+0)=senacosG+cosasenG

cos(a+0)=cosacos© - senasen9

tan(a + 6) = tan a + tan 9 l - t a n a t a n 9

IDENTIDADES PARA LA DIFERENCIA DE DOS ARCOS

sen(a - 9)=senacos0 - cososenG

cos(a - 9)=cosacos9+senusenG

t a n a - t a n 9 : sen ( a - 6 ) eos a eos 9

PROPIEDAD

Si x es variable angular y a y í » son constantes, entonces

asen x+ b eos x =Va 2 +b2 sen( x + Q)< donde

sen 9 = eos 9 = Va 2 + b 2 ' Va 2 +

Además, se cumple que

- V a 2 +i>2 < a s e n x + ftcosx < V a 2 + b2

TEOREMAS

IDENTIDADES AUXILIARES

sen(a+9)sen(a+9)=sen a - sen 9

cos(a+9)cos(a - 9)=eos o - sen a

tana + tan©; sen(a + 9) eos a eos 9

Si A+B+C=nn,nsZ, entonces tanA+tanfi+tanC=tanAtanñtanC

Si x + y + z = (2/7 + 1)-, neZ, 2

entonces coL4+cotñ+cotC=cotAcotBcotC

269

Academia C é s a r Vallejo, - Material Didáctico N. 1

Problemas resueltos

1. Demuestre que si x es variable real y o y b constantes reales se cumple que

-\la2+b2 <asenx + ftcosx<Va2 +b2

Demostración

Sea £=asenx+£>cosx

-> £-£>cosx=asenx

Elevamos ambos miembros al cuadrado

£ 2-2b£cosx+b 2cos 2x=a 2sen 2x

£ 2-26£cosx+£> 2cos 2x=a 2(l-cos 2x)

Simplificando, tenemos la ecuación de 2° grado:

(a 2+b 2 )cos 2x-2£í>cosx+£ 2-a 2=0

Comox E R, entonces, cosx e R. Lue­go, la ecuación cuadrática tiene solu­ciones reales, es decir, el discriminante de la ecuación es mayor o igual a cero.

( -2££0 2 -4(a 2 +b 2 ) (£ 2 -a 2 ) > 0

£ V - ( a 2 + b 2 ) ( £ 2 - a 2 ) > 0

E2b2-E2a2~E2b2+a\a2+b2) > 0

o 2 ( a 2 +b 2 ) - £ 2 o 2 >0 - » E2<a2+b2.

.: - V o 2 + 6 2 <E<4a2+b2

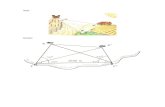
2. A partir del gráfico, halle x.

2V3

Resolución Del gráfico, se observa que

• p=a+30° x x + 7

• tanoc = —¡= tanp = —;=-2V3 ' 2V3

P=a+30° -> tanp=tan(a+30°)

tan a + tan 30° tanp =

x + 7

2S

l-tanatan30°

x J _ 2 ^ + ^

J L Y _ L 2 ^ V3

x + 7 _ V 3 ( x + 2) ^ 2V3 ~ 6 - x

Simplificando, tenemos: x 2 +7x-30=0 .

.-. x=3

270

Academia C é s a r Vallejo - Material Didáctico N. 1

Identidades trigonométricas de arcos múltiples

IDENTIDADES DEL ARCO DOBLE IDENTIDADES DEL ARCO TRIPLE

eos 29 =

eos 2 9 - s e n 2 9

2 c o s 2 6 - l

l - 2 s e n 2 9

sen29=2sen9 cosG tan 29 = 2 tan9

l - t a n 2 9

sen39=3sen9-4sen 39

cos39=4cos 39-3cos9

tan 39: 3 t an9 - t an 3 9

l - 3 t a n 2 9

Fórmulas de degradación

2cos z9=l+cos29 2sen29=s]-cos29

Triángulo del ángulo doble

l+ tan 2 9 2tan9

sen 29

• eos 29 =

l + t a n ^

l - t a n 2 6

l + tan 2 9

Identidades auxiliares

• cot9+tan9=2csc29

• cot9-tan9=2cot29

3 1 . sen 4 9 + cos 4 9 = - + -cos49

K K 5 3 • sen 6 + cos 0 = - + -cos49

4 4 5 3

:- + -< 8 8

Fórmulas de degradación

4cos,:19=3cos9+cos39

4send9=3sen9 - sen39

Identidades auxiliares

sen39=sen9(2cos29 +1)

cos39=cos9(2cos29 -1)

4sen9sen(6G° - 9)sen(6G°+9)=sen39

4cos9cos(6G°- 9)cos(6G°+9)=cos39

tan9tan(60°-9)tan(60°+9)=tan39

Propiedad

V n e Z, donde x es variable real

se cumple que

1 < s e n 2 " x + c o s 2 n x < l

272

Semestral UNI ' T r i g o n o m e t r í a

Problemas resueltos

l . Halle el valor de la expresión 4 7t 4 371 1 TC 1 3n

sen —+sen —+-eos— + - e o s— 16 16 2 8 2 8

Resolución Sea

4 71 4 371 1 7t 1 3jl K = sen — + sen —+-eos— + - e o s—

16 16 2 8 2 8

Recuerde que

x sen—

2

1-cosx 1+cosx

n sen— = '

16

371 1-cos— o 1-cos 8 37t 9 2-; s en— = \2 16 V 2

Reemplazando en K

K--1-cos 1-cos

3n

1 7t 1 3n + - C O S — + - C O S

2 8 2 8

K = 1 - C O S

V

, 37t 1-cos

V

1 71 1 3ít - - C O S - I - - C O S —

2 8 2 8 i r . 7C 2n 1 n 3lt 9 37C l-2cos-+cos - l-2cos—+cos —

K= § §•+ § 8-+

1 Ji l 3TT + - C O S — + - C 0 S —

2 8 2 8

.. I l ( 9 t 2 3TC K = - + - cos z - + eos¿ —

2 4^ 8 8

_ 3TC 7C Pero eos—=sen—

Luego, K= — + —\s - + sen -s 2 4^ 8 8

.-. Á=3/4

Simplifique la expresión

sen 3 x eos 3 x l + -

sen3x cos3x 2 UNI 2 005-II

Resolución Sea

sen 3 x eos 3 x l : + _ sen3x cos3x 2

Multiplicando por 4

4sen 3 x 4cos 3 x „ 4E = + 2

sen3x cos3x

Recuerde que

4sen 3x=3senx- sen3x 4cos 3x=cos3x+3cosx

Reemplazando

. „ 3senx-sen3x cos3x + 3cosx „ 4£ = + 2

sen3x cos3x

_ 3senx _ ^ _ ^ _ 3 eos x + ^ sen3x cos3x

4E = 3 _ J senx cosx

i sen3x cos3x

4£ = 3 sen(x - 3x)

sen3xcos3x

Luego

E =

3sen(-2x) 2(2sen3xcos3x)

-3sen2x 2sen6x

E = —sen2xcsc6x 2

273

Semestral UNI • T r i g o n o m e t r í a

Transformaciones trigonométricas

DE SUMA O DIFERENCIA DE DOS SENOS O COSENOS A PRODUCTO

Por identidades trigonométricas de arcos compuestos Para el seno se tiene:

sen(a+p)=senacosp+cosasenp

sen(a - p)=senacosp - cosasenp

Al sumar y restar el primer y segundo miem­bro obtenemos:

sen(a+p)+sen(a- P)=2senacosp

sen(a+p) - sen(a - P)=2cosasenp

SeaA=a+p y tí=a-p, entonces

A + B . A-B a = y 6 =

2 2

Reemplazando, en las expresiones, se tiene

. _ _ ,A+B) (A-B sen A + sen B = 2 sen eos

2 2

, o o I A + B ) ( A ~ B

senA-sentí = 2cos sen 2 2

D „ (A+B) (A-B) 5/4 + cosñ = 2cos eos

l 2 J { 2 )

. _ „ ,A + B) (A-B^ eos A-eos tí = -2 sen sen

2 2 ,

DE PRODUCTO DE DOS SENOS O COSENOS A SUMA O DIFERENCIA

2senxcosy=senO+y)+sen(jr-y)

2cosxcosy=cos(x+y)+cosCx-y)

2serurseny=cos(x -y ) - cosCx+y)

De manera análoga se deduce que

Propiedades

Si A+B+C=n, se cumple

A D r A A B C

sen A + sen tí + sen C = 4 eos—eos—eos— 2 2 2

A D ^ A A B C 1 eos /i + eos tí+eos C = 4 sen—sen—sen—+1

2 2 2

sen2A+sen2tí+sen2C=4senAsentísenC

cos24+costí+cos2C=- 4co&4costícosC-1

275

Academia C é s a r Vallejo Material Didáctico N.° 1

Problema resuelto

Demuestre que senx+sen(x + r ) + sen(x + 2r) + . . .+sen(x+(n- l ) r ) = ^2-^senl p + t r

Donde

P: primer ángulo U: último ángulo r. razón de la progresión n: número de términos

Demostración

Sea £=senx-+sen(x+r)+sen(x+2r)+...+sen(x+ (n - 1 )r)

Multiplicamos por 2 s e n ^ j a ambos miembros

2£sen - =2senxsen - +2sen(x+r)sen - +...+2sen(x+(/7-l)r)sen -{2J {2J [2J [2

Cada término del segundo miembro lo transformaremos en una diferencia de cosenos.

2senxsen - =cos x - - | -cos U J l 2

2sen(x + r )sení^|=cosí x ^ -

/ 2

-eos 3/

2sen(x + 2r)sen| - j=cos| ^ (

-eos x + 2

2sen(x + (n-í)r)sen| - | = cos x+| n - - ' ! |r -cosí x+ f n — I r l l 2 j

Sumando todos los términos de manera vertical

2£ s e n ^ j = cos|^x-:~ j - cosí x + ^ n - ^ 1 r

Transformando a producto:

ÍEsen ^ | = /2'sen X + n-— \r+\ —

2 2 sen

, n i r

x+\ r - x - -2 2

2sen|4 |£ = 2sen| \ J

Sea: P=x

Reemplazando

M+{x+(.n-dr)\Jnr

U=x+(n-\)r

sen

sen

2 J ÍP + U

276