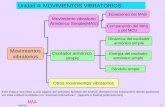
Oscilador Armónico (Simple y Amortiguado)

8/18/2019 Oscilador Armónico (Simple y Amortiguado)

1/8

Álvaro García Corral

1

Resolución de la EDO del osciladorarmónico simple y amortiguado

Un oscilador armónico es un sistema en el que siempreactúa una fuerza, que es recuperadora, es decir, del tipo , también pueden actuar otras fuerzas pero lafuerza fundamental que caracteriza al oscilador armónicoes la recuperadora.

Se observa que el problema que vamos a tratar esunidimensional (en el espacio) y que el sistema dereferencia se ha tomado de forma que la posición de

equilibrio se ha tomado en el origen , la fuerzarecuperadora es nula en la posición de equilibrio. Ahora aplicamos la segunda ley de Newton, quedándonosla siguiente EDO:

̈ ̈

Esta es la EDO que rige el movimiento del osciladorarmónico simple, en el que la única fuerza presente es larecuperadora.

Llamamos a la constante por razones que

entenderemos después, quedándonos:

̈ Recordamos que para resolver EDOs de este tipo(homogéneas, con la derivada segunda y la función), lasolución era una exponencial, un seno, un coseno, o unacombinación de los dos últimos.


2/8


2

Para hallar la solución general lo más cómodo es comenzarconjeturando que la solución tiene la forma exponencial, ydespués de haberlo resuelto, aplicar la fórmula de Eulerpara hallar la forma de las demás soluciones.

Conjeturamos la forma exponencial de la solución, con unparámetro y una constante de integración :

̇ ̈ Y ahora sustituimos en la EDO, para hallar el valor denuestro parámetro :

̈

Obtenemos dos valores posibles para el parámetro por loque la solución general será la suma de dos exponencialesimaginarias, cada una con uno de los valores de y unaconstante de integración diferente.

Por supuesto que

y

son números complejos, sin

embargo, nuestra función solución tiene que ser unafunción real, veremos cómo se consigue esto, pero antesvamos a ver como se pasa a las otras soluciones.


3/8


3

Para desarrollar las exponenciales utilizamos la fórmula deEuler:

( ) ( ) Ahora introduzcamos el hecho de que y son númeroscomplejos de manera que:

Sustituyendo en la ecuación anterior obtenemos:

( ) ( ) ( ) ( )

Podemos dividir la solución en parte real y parte imaginaria:

Dividimos la solución en parte real y parte imaginaria, y porlas propiedades de la EDO, tanto la parte real como la

parte imaginaria son solución por si solas, de manera quela solución que se corresponde con la realidad sería laparte real.

Esta solución es en cualquier caso un poco extraña, porquesólo hay una derivada segunda, pero tenemos cuatroconstantes de integración: y


4/8


4

Veamos qué pasa si imponemos que y fuerancomplejos conjugados el uno del otro:

Al sustituir en la ecuación tendríamos:

Y así, la solución imaginaria se anula y obtenemos lasolución que sirve para interpretar el caso real:

De esta manera sólo quedan dos constantes deintegración, correspondientes a integrar dos veces conrespecto al tiempo, lo que implica que las constantescomplejas que multiplican a las dos exponenciales soncomplejos conjugados el uno del otro.


5/8


5

También podemos poner la solución como un seno o uncoseno con un desfase, quedando la solución general:

Si desarrollamos el seno de la suma y el coseno de lasuma:

Por lo tanto:


6/8


6

Para el caso del oscilador armónico amortiguado, tenemosque añadir otro término a la EDO del oscilador armónicosimple, este término se corresponde con una fuerza derozamiento y es proporcional a la velocidad:

̈ ̇ Donde siendo el coeficiente de rozamiento oviscosidad.

Entonces recordamos que para EDOs homogéneas en lasque aparecen derivadas de orden par e impar, una solución

va a ser siempre la exponencial:

̇ ̈ Aplicándolo a la EDO:

̈ ̇ √ √ En el ejercicio del oscilador armónico simple , en esteejercicio es mayor que cero pero poco, por lo que

consideramos que

En nuestra solución quedan entonces dos exponenciales:

[ ] Igual que en el caso anterior

y

son números

complejos.


7/8


7

Ahora aplicamos la fórmula de Euler, para obtener lasolución en forma de senos y cosenos:

Sin embargo solo nos interesa la parte real de la solución,por lo que necesitamos dividir la solución en parte real yparte imaginaria de la misma manera que en el ejercicio deloscilador armónico simple:

Si se resuelve de la misma manera, se obtiene que:

[ ] Veamos qué pasa si imponemos que y fuerancomplejos conjugados el uno del otro:


8/8


8

La solución queda de la forma

[ ] [ ]

Y así, la solución imaginaria se anula y obtenemos lasolución que sirve para interpretar el caso real:

[ ]

Oscilador Armónico (Simple y Amortiguado)

Documents

Transcript of Oscilador Armónico (Simple y Amortiguado)