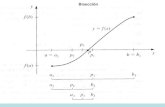
Introducción y Metodo Bisección
description
Transcript of Introducción y Metodo Bisección
-
Erika Riveros Morn
1
Resolucin de ecuaciones no lineales y Mtodo de Biseccin
Recordemos algunas ecuaciones
1) Resolver [ ] [ ] Sol:
2) Resolver la siguiente ecuacin literal para la variable ;
Sol:
3) Resolver
Solucin:
En este caso
[ ] [ ]
4) Resolver
No es posible despejar la variable por los mtodos algebraicos conocidos, para obtener su
solucin recurriremos a mtodos numricos
Un problema fundamental de las matemticas aplicadas es determinar valores tal que
Estos valores se denominan races de la ecuacin .
En general no es posible resolver una ecuacin como esta y por lo tanto encontrar los valores exactos
no es alcanzable en todos los casos, por esto se han desarrollados mtodos que permiten determinar las
aproximaciones numricas suficientemente cercana a las races buscada.
El siguiente ejemplo ilustra el tipo de problemas que queremos estudiar
Problema:
En los estudios sobre recoleccin de energa solar al enfocar un campo de espejos planos en un colector
solar central, un investigador obtuvo la siguiente ecuacin para el factor de concentracin geomtrica C.
Donde A es el ngulo de anillo del campo, F es la cobertura fraccionaria del campo con los espejos, D es el
dimetro del colector y h es la altura del mismo.
Encuentre A, si h=300, C=1200, F=0,8 y D=14.
Para resolver este tipo de problemas consideremos 3 mtodos que ilustran el tipo de argumentos y
herramientas usadas en el clculo numrico.
-
Erika Riveros Morn
2
Dada una funcin , resolver una ecuacin de la forma es hallar todos los valores
que anulan dicha funcin.
A dichos valores se les denomina races o soluciones de la ecuacin, tambin se les llama ceros de la
funcin
Previo:
Supongamos que se tiene una ecuacin , donde la funcin f es continua en intervalo
Definicin 1:
Diremos que es una raz de la ecuacin si y solo si
Definicin 2:
Diremos que es un cero de si y solo si es una raz de
Teorema 1 (Bolzano)
Si una funcin continua asume valores de signo opuestos en los extremos de un intervalo es decir,
, entonces el intervalo contendr al menos una raz de .
El clculo aproximado de las races reales de , se efecta en dos etapas:
Etapa 1:
Establecer los intervalos ms pequeos posibles que contengan una y solo una raz de
Etapa 2:
Estimacin de la raz. Calcular la raz usando algn algoritmo con cierto grado de precisin.
-
Erika Riveros Morn
3
Etapa 1:
Debemos estimar el valor de , tal que
(Lo cual geomtricamente significa el valor de la abscisa donde la grfica de intersecta al eje X )
Un modo sera graficar la funcin , para graficar se puede apoyar en el trazado de curvas ,
aplicando derivadas.
Por ejemplo: Estimar la solucin de
La grfica de es la siguiente
Se observa que hay una interseccin con el eje , tenemos una raz real para la ecuacin y sta se
encuentra en el intervalo
Si la grfica se complica, es conveniente a veces sustituir la ecuacin por una ecuacin
equivalente de la forma:
Donde las funciones de son ms sencillas de graficar que .
Se grafican cada una de ellas en un mismo plano.
Entonces las abscisas de los puntos de interseccin de la grfica de son las races reales de
.
Pues si por lo que es raz real de
-
Erika Riveros Morn
4
Ejemplo
Determinar el nmero de races de la ecuacin y los intervalos donde ellas se encuentran
Solucin. Usando la observacin anterior, podemos expresar en la forma , haciendo
y y graficando estas funciones.
Se concluye que la ecuacin tiene dos races reales.
Para determinar los intervalos donde estn races, usamos el teorema de Bolzano.
; como ,
; como ,
-
Erika Riveros Morn
5
Mtodo de la Biseccin.
Est basado en el teorema del valor intermedio que dice: si una funcin tal que y tienen
signos distintos y adems es continua en un intervalo que concluye entonces existe tal
que .
De este modo debemos determinar dos puntos donde la funcin cambie de signo, esto es posible
mediante evaluando la funcin, de modo que supongamos que ya tenemos estos valores. Intervalo donde
se encuentra la raz.
El mtodo consiste en considerar el punto medio entre ambos extremos y determinar donde se
produce el cambio de signo, en o en segn corresponda
Se descarta uno de los dos intervalos y se contina con el restante, al que se aplica el mismo
procedimiento. De este modo en cada iteracin del proceso la amplitud del intervalo se reduce a la mitad
y la raz buscada quedara encerrada en el intervalo restante.
El intervalo inicial tiene amplitud , de este modo, despus iteraciones, obtendremos un
intervalo de amplitud .
Este mtodo permite obtener una sucesin , donde cada , es el punto medio obtenido en cada
iteracin. Dado que la amplitud del intervalo tiende a 0, tenemos que la sucesin es convergente y su
lmite es una de las races buscadas.
Algortimo:
Tenemos que ,
evaluamos
Se pueden presentar 3 situaciones:
1) Si , por lo que es raz
2) Si entonces ;
3) Si entonces ;
-
Erika Riveros Morn
6
Nota 1
Usualmente el control de parada en el mtodo de la biseccin es | | , en donde
si la aproximacin pedida es cifras decimales exactas.
Teorema
El numero de iteraciones requeridas para garantizar una aproximacin a una raz de exactitud E est dada
por
, donde L es la longitud del intervalo.
Demostracin:
| |
| |
| |
| |
donde
n indica el nmero de iteraciones necesarias.
Ejemplo
1) Considere la ecuacin
a) Determine cuantas races posee la ecuacin y el intervalo de nmeros enteros
consecutivos donde se encuentra la mayor raz .
b) Determine el nmero de iteraciones necesarias para asegurar una exactitud de 8
cifras decimales en el mtodo de biseccin si [ ]
-
Erika Riveros Morn
7
c) Estimar el valor de la raz si [ ] utilizando el mtodo de Biseccin realizando 5
iteraciones y determine el nmero de cifras decimales exactas.
Respuesta:
a) Para determinar cuntas races reales tiene la ecuacin debemos graficar
y
Hay dos puntos de interseccin por lo que tenemos 2 races
b) Determinamos el intervalos donde se encuentran las races, usando teorema
Sea
Por lo que luego
c) Determine el nmero de iteraciones necesarias para asegurar una exactitud de 10
cifras decimales en el mtodo de biseccin y usando el intervalo encontrado en b)
Para obtener el nmero de iteraciones usamos la frmula
| | , ,
,
, ,
Se necesitan 34 iteraciones
-
Erika Riveros Morn
8
d) Calcular el valor de la raz encontrada en b) utilizando el mtodo de Biseccin con
una aproximacin de 4 cifras decimales y 4 iteraciones
i a b m f(a) f(m) f(a)*f(m) Dif
0 1 2 1.5 -0.28171817 7.3890561 neg 0.25
1 1 1.5 1.25 -0.28171817 2.73168907 neg 0.125
2 1 1.25 1.125 -0.28171817 1.05284296 neg 0.0625
3 1 1.125 1.0625 -0.28171817 0.34584185 neg 0.03125
4 1 1.063 1.03125 -0.28171817 0.02250219 neg 0.015625
5 1 1.031 1.015625 -0.28171817 -0.13195408
La mayor raz estimada corresponde a 1.03125
Para determinar con cuantas cifras decimales exacta se obtuvo, debemos agregar
una fila y as obtener | |
La raz se obtuvo con una cifra decimal exacta.