8/28/2015 1

Método de Bisección

Autar Kaw, Jai PaulIlka Banfield

2

Bases del Método

Teorema

x

f(x)

xu x

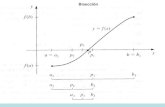
Una ecuación f(x)=0, donde f(x) es una función real y continua, posee al menos una raíz entre xl y xu sif(xl)*f(xu) < 0.

Figura 1 Existe al menos una ráiz entre los dos puntos si la función esreal, continua y cambia de signo en este rango.

8/28/2015

x

f(x)

xu x

3

Bases del Método

Figura 2 Si la función no cambia de signo entre los dos puntos, aunasí quizá exista las raíz de la ecuación entre dichos puntos.

xf

0xf

8/28/2015

x

f(x)

xu x

4

Bases del Método

Figura 3 Si la función no cambia de signo entre los puntos, quizano exista raíz de entre los puntos.

x

f(x)

xu

x

xf

0xf

8/28/2015

x

f(x)

xu x

5

Bases del Método

Figura 4 Si la función cambia de signo entre los dos puntos, quiza exista más de una raíz para la ecuación entre los puntos.

xf

0xf

8/28/2015

6

Algoritmo del Método de Bisección

8/28/2015

7

Paso 1

Seleccionar x y xu como dos posibles raices de maneraque cumplan con que f(x) f(xu) < 0, o lo que es lo mismo que f(x) cambia de signo entre x y xu. Figura 5.

x

f(x)

xu x

Figura5

8/28/2015

x

f(x)

xu x

xm

8

Paso 2

Estimar la raíz, xm de la ecuación f (x) = 0 como el puntomedio entre x y xu

xx

m = xu

2

Figure 6 Estimate of xm

8/28/2015

9

Paso 3

Luego debe verificar los siguiente

a) Si , la raíz se encuentra entre x y xm; asignamos x = x ; xu = xm.

b) Si , la raíz se encuentra entre xm y xu; asignamos x = xm; xu = xu.

c) Si ; la raíz es xm. Y se detiene la búsqueda.

0ml xfxf

0ml xfxf

0ml xfxf

8/28/2015

10

Paso 4

xx

m = xu

2

100

new

m

old

m

new

ax

xxm

raíz la de estimación actual new

mx

raíz la de previa estimaciónold

mx

Encuentra la nueva estimación

Encuentra el valor absoluto de el error aproximado relativo

donde

8/28/2015

11

Paso 5

Si ?

Si

No

Ir al paso 2 utilizandolos nuevos valores Xu y

Xl

Deterner el algoritmo

Compare el valor absoluto del error relativo aproximadocon la error tolerado especificado .

a

s

sa

Es importante saber si el número de iteracción llega al máximo, en ese caso esto debe detener el algoritmo y notificar al usuario.

8/28/2015

12

EjemploUsted trabaja para una compañia que fabrica baños,especificamente con el mecanismo de llenado y vacíadodel tanque del bater. La boya flotante tiene unagravedad específica de 0.6 y un radio de 5.5 cm. Debesdeterminar la profundida que la boya está sumergidacuando flota en el agua.

Figure 7 Diagrama de la boya flotante8/28/2015

13

Ejemplo 1 Cont.

La ecuación de la profundidad que la boya se sumergees:

a) Utilice el método de bisección y estima la raíz con tresiteracciones.

b) Encuentre el valor absoluto del error relativo aproximadode cada iteracción y el número de digitos significantescorrectos en cada iteracción.

010993.3165.0 423 xx

8/28/2015

14

Ejemplo 1 Cont.

De la física del problema la bola de estar sumergida entre x = 0 y x = 2R,

donde R = radio de la boya,

lo que es.

11.00

055.020

20

x

x

Rx

Figure 6 Diagram of the floating ball

8/28/2015

Gráfico de la función:

15

Ejemplo 1 Cont.

423 1099331650 -.x.xxf

Figure 8 Gráfico de la función (x)

Solution

8/28/2015

16

Ejemplo 1 Cont.

Asumimos

11.0

00.0

ux

x

Determinar si la función cambia de signo entre x and xu .

4423

4423

10662.210993.311.0165.011.011.0

10993.310993.30165.000

fxf

fxf

u

l

Dado

010662.210993.311.00 44 ffxfxf ul

Al menos existe una raíz entre x y xu, lo que es entre 0 y 0.11

8/28/2015

17

Ejemplo1 Cont.

Figure 8 Grafico de cambio de signo

8/28/2015

18

Example 1 Cont.

055.02

11.00

2

u

m

xxx

010655.610993.3055.00

10655.610993.3055.0165.0055.0055.0

54

5423

ffxfxf

fxf

ml

m

Iteration 1The estimate of the root is

Hence the root is bracketed between xm and xu, that is, between 0.055 and 0.11. So, the lower and upper limits of the new bracket are

At this point, the absolute relative approximate error cannot be calculated as we do not have a previous approximation.

11.0 ,055.0 ul xx

a

8/28/2015

19

Example 1 Cont.

Figure 9 Estimate of the root for Iteration 1

8/28/2015

20

Ejemplo1 Cont.

0825.02

11.0055.0

2

u

m

xxx

010655.610622.1)0825.0(055.0

10622.110993.30825.0165.00825.00825.0

54

4423

ffxfxf

fxf

ml

m

Iteración 2La estimación de la raíz es

Dado que la raíz está entre x y xm, lo que es, entre 0.055 y 0.0825, se sustituyen los límites:

0825.0 ,055.0 ul xx

8/28/2015

21

Ejemplo 1 Cont.

Figure 10 Estimación de la raíz en la iteracción 2

8/28/2015

22

Ejemplo1 Cont.

El valor absoluto del error aproximado en la iteracción 2 isa

%333.33

1000825.0

055.00825.0

100

new

m

old

m

new

ma

x

xx

Ningún digito significativo es cierto en la respuesta de xm = 0.0825 debido a que el erro es mayor que del 5%.

8/28/2015

23

Ejemplo 1 Cont.

06875.02

0825.0055.0

2

u

m

xxx

010563.510655.606875.0055.0

10563.510993.306875.0165.006875.006875.0

55

5423

ffxfxf

fxf

ml

m

Iteración 3La estimación de la raíz es

Dado que la raíz se encuentre entre x and xm, lo que es, entre 0.055 y0.06875, estos son los nuevos límites

06875.0 ,055.0 ul xx

8/28/2015

24

Ejemplo 1 Cont.

Figure 11 Estimación de la raíz, iteracción 3

8/28/2015

25

Ejemplo 1 Cont.

El valor absoluto del error aproximado al final de la iteracción 3a

%20

10006875.0

0825.006875.0

100

new

m

old

m

new

ma

x

xx

Aún no hay digitos significativos, el error es mayo que 5%. Sieteiteracción son mostrada en la tabla No.1

8/28/2015

26

Tabla 1

Table 1 Raíz de f(x)=0 como función dél número de iteracción para el método de bisección.

Iteration x xu xm a % f(xm)

1

2

3

4

5

6

7

8

9

10

0.00000

0.055

0.055

0.055

0.06188

0.06188

0.06188

0.06188

0.0623

0.0623

0.11

0.11

0.0825

0.06875

0.06875

0.06531

0.06359

0.06273

0.06273

0.06252

0.055

0.0825

0.06875

0.06188

0.06531

0.06359

0.06273

0.0623

0.06252

0.06241

----------

33.33

20.00

11.11

5.263

2.702

1.370

0.6897

0.3436

0.1721

6.655×10−5

−1.622×10−4

−5.563×10−5

4.484×10−6

−2.593×10−5

−1.0804×10−5

−3.176×10−6

6.497×10−7

−1.265×10−6

−3.0768×10−7

8/28/2015

27

Ejemplo 1 Cont.

Para encontre la cantidad de números signficativos al menos correctosen la respuesta luego de 10 iteracciónes:

463.23442.0log2

23442.0log

103442.0

105.01721.0

105.0

2

2

2

m

m

m

m

m

a

2mDe manera que

El número de digitos significativos correctos en la respuesta del error estimado 0.06241 al final de la 10th iteración es 2.

8/28/2015

28

Ventajas del Método

Siempre converge

El rango de busqueda de la raíz se reduce a la mitad con cada iteracción

8/28/2015

29

Inconvenientes

Convergencia lenta

Si un de los valores asumidosinicialmente esta cerca de la raíz la convergencia es más lenta.

8/28/2015

30

Inconvenientes (cont)

Si una función f(x) es de tal forma quetoca al eje x, en un valor mínimo de todala función es incapaz de encontrar valoresiniciales para la búsqueda.

f(x)

x

2xxf

8/28/2015

31

Inconvenientes (cont.)

La función cambia de signo pero la raízno existe.

f(x)

x

x

xf1

8/28/2015