El Triángulo de Pascal
23
El Triángulo de Pascal El triángulo aritmético
description
Presentación para niños de algunas de las propiedades que esconde en triángulo aritmético de Pascal.
Transcript of El Triángulo de Pascal
El Triángulo de
PascalEl triángulo aritmético
Es
el t
riángulo
más
fam
oso
de la
s M
ate
máti
cas• Siglo XVI Petrus Alpinus
• Siglo XII Omar Khayyam
• Siglo XIII Yang Hui
• 1654 Blaise Pascal
Construcción del triángulo
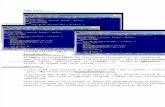
El triángulo se construye desde la cúspide hacia abajo. El primer elemento es el número 1, formando la fila 0. La fila 1 está formada por dos elementos, ambos el número 1. A partir de aquí, cada fila está formada por un elemento más a la anterior. Siempre el primero y último son el 1, y los interiores el resultado de la suma de los dos elementos que se sitúan encima de él y adyacentes a la fila superior.
1 1 1 1 2 1 1 3 3 1 1 4 6 4 11 5 10 10 5 1 ...
Fila 0
Fila 1
Fila 2
Fila 3
Completa tu triánguloObserva y analiza el triángulo
¿Encuentras alguna propiedad a simple vista?
Segunda
dia
gonal
Terc
era
dia
gonal
Núm
ero
s tr
iangula
res
Cuart
a d
iagonal
Núm
ero
s te
traédic
os
En las matemáticas un número tetraédrico , o número piramidal triangular, es un número figurado que representa una pirámide de base triangular y tres lados, llamada tetraedro. El n-ésimo número tetraédrico es la suma de los primeros n números triangulares.
Los primeros números tetraédricos son: 1, 4, 10, 20, 35,
56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969, …
Sum
as e
n
dia
gonal
¿Encuentras alguna regularidad?
¿cuanto vale la suma de los nº naturales
del 1 al 10?
El s
tick
de
hock
ey
¿Cuánto vale la suma
de los 13 primeros nº triangulares?
¿Cuánto vale la suma
de 1,6,21,56,126 y
462? Localízalos en el triángulo y da la
respuesta de forma
automática sin hacer la suma
Los
núm
ero
s pri
mos
Si el primer elemento de una fila es un
número primo, todos los números de esa fila
serán divisibles por él (menos el 1, claro).
Así, en la fila 7: (1 7 21 35 35 21 7 1), los
números 7,21 y 35 son divisibles por 7.
Más
sorp
resa
s
Si sumas los números de cada
fila, ¿Qué números obtienes?
Otra
pro
pie
dad
curio
sa
Observa las primeras
filas como si fueran un
solo número:
1, 11, 121, 1331 y
14641
¿A qué corresponden estos
números?
La m
arg
ari
ta d
e
Pasc
al
Seri
e d
e
Fibonacc
i
La serie de Fibonacci puede
ser encontrada también en
el triángulo de Pascal.
Dividiendo al mismo según
las líneas que mostramos
en el diagrama, los números
atrapados entre ellas
suman cada uno de los
elementos de esta sucesión.
Recordemos que esta
sucesión (que, por cierto, se
construye de manera
similar al triángulo de Pascal), es:
1,1,2,3,5,8,13,21,...
Suce
sión d
e
Fibonacc
i
Fibonacc
i en e
l m
undo v
egeta
l
La distribución de las
hojas alrededor del tallo
de las plantas . El número de espirales en
numerosas flores y frutos
también se ajusta a parejas consecutivas de
términos de esta sucesión.
Cualquier variedad de
piña presenta siempre un
número de espirales que
coincide con dos términos
de la sucesión de Fibonacci, 8 y 13; o 5 y 8
Fibonacci e
n e
l mundo
anim
al
La reproducción
de los conejos
responde a esta
sucesión.
Espiral Durero,
una espiral, que
de forma bastante
ajustada, está
presente en el
crecimiento de las
conchas de los
moluscos, en los
cuernos de los
rumiantes... Es
decir, la espiral
del crecimiento y
la forma del reino
animal.
La m
arg
ari
ta d
e
Pasc
al
Escribe los 6 números
que rodean a 4. Calcula su multiplicación ¿Es el resultado el cuadrado de un nº natural? ¿Cuál?
¿Cómo se puede obtener ese número
multiplicando algunos
nº que rodean a 4?
Sigue investigando porque hay más información en este
triángulo.
