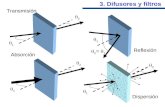
3 Filtros Covolucion y Morfologia

Procesamiento de Imgenes

3. Filtros y transformaciones locales.

Tema 3. Filtros y

transformaciones locales.

3.1. Filtros y convoluciones.3.2. Suavizado, perfilado y bordes.3.2. Suavizado, perfilado y bordes.3.3. Filtros no lineales.3.4. Morfologa matemtica.

3.1. Filtros y convoluciones.

Recordatorio: en las transformaciones globales, cada pxel de salida depende slo de un pxel de entrada.

90 67 75 7892 87 78 8245 83 80 13039 69 115 154

62 68 78 81102 89 76 8583 109 80 11169 92 115 120

Transf. global

Transf. localEntrada Salida

No se tiene en cuenta la relacin de vecindad entre pxeles. El resultado no vara si los pxeles son permutadosaleatoriamente y despus reordenados.

Transformacin local: el valor de un pxel depende de la vecindad local de ese pxel.

Transf. localEntrada Salida


Transformacin global:R(x,y):= f(A(x,y)) R(x,y):= f(A(x,y), B(x,y))

Filtros y transformaciones locales:R(x,y):= f(A(x-k,y-k), ..., A(x,y), ..., A(x+k,y+k))

Ejemplo. Filtro de la media. Ejemplo. Filtro de la media.R(x,y):= (A(x-1,y-1)+A(x,y-1)+A(x-1,y)+A(x,y))/4

92 78 8245 80 13039 115 154

- - -

- 74 93- 70 120 / 4

A R

3.1. Filtros y convoluciones. Ejemplo. Entrada, A Salida, R

Resultado: la imagen se suaviza, difumina o emborrona. Resultado: la imagen se suaviza, difumina o emborrona. Las transformaciones locales tienen sentido porque existe

una relacin de vecindad entre los pxeles. Recordatorio: un pxel representa una magnitud fsica en

un punto de una escena dos pxeles prximos corresponden a puntos cercanos de la escena el mundo es continuo los pxeles prximos tendrn valores parecidos.

3.1. Filtros y convoluciones. Un tipo interesante de transformaciones locales son las

convoluciones discretas. Convolucin discreta: transformacin en la que el valor

del pxel resultante es una combinacin lineal de los valores de los pxeles vecinos en la imagen.

Ejemplo. El filtro de la media es una convolucin.R(x,y):= 1/4A(x-1,y-1) + 1/4A(x,y-1) + 1/4A(x-1,y) + 1/4A(x,y)R(x,y):= 1/4A(x-1,y-1) + 1/4A(x,y-1) + 1/4A(x-1,y) + 1/4A(x,y)

Otra forma de ver la convolucin:Matriz de coeficientes de lacombinacin lineal. 1/4 1/4

1/4 1/4

(x-1,y-1) (x,y-1)

(x-1,y) (x,y)

3.1. Filtros y convoluciones. La matriz de coeficientes es conocida como la mscara o

ncleo (kernel) de convolucin. Idea intuitiva: se pasa la mscara para todo pxel de la

imagen, aplicando los coeficientes donde correspondan.

1/4 1/4

Mscara de convolucin

Cunto valen 1/4 1/4

92 78 82

45 80 130

39 115 154

- - -

- 74 93

- 70 120

Imagen de entrada, A Imagen de salida, R

Cunto valen estos pxeles?

+R(2,2):= 1/4(92) + 1/4(78) + 1/4(45) + 1/4(80)=


Sea M una mscara de convolucin. Se puede definir como array [-k...k, -p...p] de real

Algoritmo. Clculo de una convolucin.Denotamos la convolucin como: R:= MA

Entrada. A: imagen de maxX x maxY

En X la mscara va de -k a k, y en

Y de -p a p. El punto central es

(0,0)M: array [-k...k, -p...p] de real

Salida. R: imagen de maxX x maxY Algoritmo:

para cada pxel (x, y) de la imagen A hacerR(x, y):= M(i, j)A(x+i, y+j)

i=-k..k j=-p..p

3.1. Filtros y convoluciones. Ejemplos. R:= MA

1/9 1/9 1/91/9 1/9 1/91/9 1/9 1/9

El valor de un pxel es la media de los 9

1 1 1

1 1 1

1 1 1

1/9

Igual que antes, pero factorizamos el mltiplo

-1 1

Restar al pxel el valor del pxel

M1 M1 M2Punto central o ancla (anchor)

es la media de los 9 pxeles circundantes

factorizamos el mltiplo comn (suma total = 1)

valor del pxel de la izquierda

A R R

3.1. Filtros y convoluciones. Sobre una imagen se pueden aplicar sucesivas

operaciones de convolucin: ...M3(M2(M1A))) A R R

Ojo: la combinacin de convoluciones es equivalente a una sola convolucin:

M2(M1A) = MA

Mscara de media aplicada 4 veces

Mscara de media + mscara de resta

3.1. Filtros y convoluciones. Cmo calcular el resultado de la combinacin? Respuesta: comprobar el efecto sobre una imagen slo

con el pxel central a UNO (seal impulso).0 0 0 0 00 0 0 0 00 0 1 0 00 0 0 0 0

1/9 =1 1 1

1 1 1

1 1 1

-1 1Mscara

equivalente0 0 0 0 00 0 0 0 0

0 0 0 0 00 1 1 1 00 1 1 1 00 1 1 1 00 0 0 0 0

1/9 = 1/9

0 0 0 0 00 1 0 0 -10 1 0 0 -10 1 0 0 -10 0 0 0 0

1 1 1

-1 1

equivalente

3.1. Filtros y convoluciones. Anlogamente, algunas convoluciones se pueden obtener

combinando otras ms simples: ncleos separables. Ejemplo.

1 1 1

1 1 1

1 1 1

A = 1/91

11/3 1 1 1 1/3 A

Resultado: el filtro de la media es separable. En lugar de aplicar una mscara de 3x3 se pueden

aplicar dos mscaras de 1x3 y 3x1 (mscarasunidimensionales).

Puede ser til para hacer los clculos ms eficientes.

1 1 11


Qu hacer con lospxeles de los bordes?

Posibilidades:1. Asignar un 0 en el resultado a los

pxeles donde no cabe la mscara.

2. Suponer que los pxeles que se salen

1/4 1/4

1/4 1/4

9 4 8

7 8 4

3 2 2

0 0 00 7 60 5 4

2 3 3

2. Suponer que los pxeles que se salen tienen valor 0 (u otra constante).

3. Modificar la operacin en los pxeles que no caben (variar el multiplicador).

4. Suponer que la imagen se extiende por los extremos (p.ej. como un espejo).

2 3 34 7 62 5 4

9 6 68 7 65 5 4 5 4 4

7 7 68 5 4

3.1. Filtros y convoluciones. Las convoluciones son una discretizacin de la idea de

convolucin usada en seales. (Repasar teora de seales...)

Diferencias: las convoluciones usadas aqu son discretas y bidimensionales.

Idea: las mscaras de convolucin son matrices de nmeros se pueden considerar, a su vez, como imgenes.imgenes.

Propiedades: Asociativa: M2(M1A) = (M2M1)A Conmutativa: M2M1A = M1M2A Ojo: al aplicar una convolucin puede ocurrir saturacin

de pxeles. Si ocurre esto, el orden s que puede ser importante.

3.2. Suavizado, perfilado y bordes.

Aplicando distintos operadores de convolucin es posible obtener diferentes efectos: Suavizado: o difuminacin de la imagen, reducir

contrastes abruptos en la imagen. Perfilado: resaltar los contrastes, lo contrario al

suavizado. Bordes: detectar zonas de variacin en la imagen. Bordes: detectar zonas de variacin en la imagen. Deteccin de cierto tipo de caractersticas, como

esquinas, segmentos, etc.

Suavizado y perfilado son ms habituales en restauracin y mejora de imgenes.

Bordes y deteccin de caractersticas suelen usarse ms en anlisis de imgenes.

3.2.1. Operadores de suavizado.

El operador de suavizado ms simple es la convolucin de media (media aritmtica).

Parmetros del operador: Ancho y alto de la regin en la que se aplica: w x h. Posicin del ancla.

Normalmente, w y h son impares y el ancla es el pxel central.central.

La mscara esun simple arrayde unos detamao wxh.

1 1 11 1 11 1 1

1 1 1 1 11 1 1 1 11 1 1 1 11 1 1 1 11 1 1 1 1Mscara de

media de 3x3 Media de 5x5

3.2.1. Operadores de suavizado. Cuanto mayor es la mscara, mayor es el efecto de

difuminacin de la imagen.

M

e

d

i

a

d

e

5

x

5

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

(

3

4

0

x

2

3

0

)

M

e

d

i

a

d

e

5

x

5

M

e

d

i

a

d

e

1

1

x

1

1

M

e

d

i

a

d

e

2

1

x

2

1

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

+


Ventajas (respecto a otros suavizados): Sencillo y rpido de aplicar. Fcil definir un comportamiento para los pxeles de los

bordes: tomar la media de los pxeles que quepan. Recordatorio: el operador de media es separable.

1 1 1 1 1 11 1 1 1 11 1 1 1 11 1 1 1 11 1 1 1 11 1 1 1 1

Media de 5x5Total: 25 sumas o(n2)

1 1 1 1 1

11111

Media de 5x1 y de 1x5Total: 10 sumas o(2n)

3.2.1. Operadores de suavizado. En algunos casos puede ser interesante aplicar

suavizados direccionales: horizontales, verticales o en cualquier direccin.

0 0 10 1 01 0 0Media horizontal 5 pxeles

1 1 1 1 1

111

Media vertical 3p Media diagonal 3pMedia vertical 3p Media diagonal 3p

M

e

d

i

a

h

o

r

i

z

.

3

1

p

M

e

d

i

a

v

e

r

t

.

3

1

p


Ejemplo 1. En una aplicacin trabajamos con imgenes capturadas de TV. El canal tiene muchas interferencias, que provocan una oscilacin cada 7 pxeles horizontales.Cmo reducir el efecto de las interferencias?

Idea: Probar con una media horizontal de 7 pxeles...

3.2.1. Operadores de suavizado. Aplicacin de media horizontal de 7 pxeles. 1 1 1 1 1 1 1

3.2.1. Operadores de suavizado. Ejemplo 2. Entrelazado de vdeo: para aumentar la

frecuencia de refresco del vdeo se separan las lneas pares y las impares (1 campo (field)=1/2 imagen). Al capturar una imagen, se mezclan los campos produciendo efectos raros.

25 imgenes/seg. 50 campos/seg. 20 mseg.

entre campos

3.2.1. Operadores de suavizado. Duplicar las filas pares (o las impares) y luego aplicar

una media vertical de 2 pxeles (para interpolar).11

Duplicadas filas paresImagen entrelazada Suavizado vertical (interp.)

3.2.1. Operadores de suavizado. Ejemplo 3. Efecto de niebla. Dada una imagen bien

definida, queremos simular una niebla (objetivo empaado). Idea: calcular una media ponderada entre la imagen original

y un suavizado gaussiano de la imagen.B. Suaviz. gauss. 40x40A. Imagen original Suma: 0,3A+0,7B

Se puede conseguir el mismo resultado con una sola convolucin. Cul sera la mscara equivalente?

3.2.1. Operadores de suavizado. Cuando se aplica la media con tamaos grandes se

obtienen resultados artificiosos (a menudo indeseados).

S

u

a

v

i

z

a

d

o

d

e

m

e

d

i

a

G

a

u

s

s

i

a

n

a

Motivo: la media se calcula en una regin cuadrada. Sera mejor aplicarla

a una regin redonda.

O, mejor, usar suavizado gaussiano...S

u

a

v

i

z

a

d

o

d

e

0 0 1 1 1 0 00 1 1 1 1 1 01 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 10 1 1 1 1 1 00 0 1 1 1 0 0


Suavizado gaussiano: media ponderada, donde los pesos toman la forma de una campana de Gauss.

Ejemplo. Suavizado gaussiano horizontal.Campana de Gauss

f(x) = e -x2/s2Campana discreta

1 6 15 20 15 6 1

s2 es la varianza

1/64

+


La varianza, s2, indica el nivel de suavizado. Varianza grande: campana ms ancha, ms suavizado. Varianza pequea: campana ms estrecha, menos

suavizado. Se mide en pxeles.

Clculo de la mscara gaussiana (1D): calcular la funcin, discretizar en el rango, discretizar en el valor y funcin, discretizar en el rango, discretizar en el valor y calcular el multiplicador...

No existe una forma ms rpida? Idea: el tringulo de Pascal.

11 1

1 2 11 3 3 1

1 4 6 4 11 5 10 10 5 1


Magia! Las filas del tringulo de Pascal forman discretizaciones de la campana de Gauss.

1 2 1

1 11/2

1/4

1 6 15 20 15 6 1

1 5 10 10 5 1

1 4 6 4 1

1 3 3 11/8

1/16

1/32

1/64

Por qu ocurre as? Recordar el teorema central del lmite...

3.2.1. Operadores de suavizado. Normalmente, el suavizado gaussiano se aplica en dos

dimensiones. Los pesos de la mscara dependen de la distancia al pxel central.

1 2 12 4 2

Campana de Gauss 2Df(x,y) = e-(x2+y2)/s2

1/16

Mscara gaussiana de 3x3

2 4 21 2 1

1/16

1: blanco0: negro

3.2.1. Operadores de suavizado. Propiedad interesante: el filtro gaussiano es separable. Resultado: se puede obtener un suavizado 2D aplicando

dos mscaras gaussianas bidimensionales, una horizontal y otra vertical.

1 2 12 4 2 1 2 1

121

1 2 1 1

3.2.1. Operadores de suavizado. Comparacin: media y suavizado gaussiano, 2D.

M

e

d

i

a

d

e

1

1

x

1

1

M

e

d

i

a

d

e

2

1

x

2

1

G

a

u

s

s

i

a

n

a

2

1

x

2

1

G

a

u

s

s

i

a

n

a

4

1

x

4

1

+

3.2.1. Operadores de suavizado. Comparacin: media y suavizado gaussiano, 1D.

M

e

d

i

a

h

o

r

i

z

.

3

1

p

M

e

d

i

a

v

e

r

t

.

3

1

p

G

a

u

s

s

i

a

n

a

6

1

x

1

G

a

u

s

s

i

a

n

a

1

x

6

1


Resultados de la comparacin: Para conseguir un mismo grado de suavizado la

mscara gaussiana debe ser de mayor tamao. Se puede tomar como medida la varianza de la mscara correspondiente.

El efecto del suavizado gaussiano es ms natural (ms El efecto del suavizado gaussiano es ms natural (ms similar a un desenfoque) que la media. Suele ser ms habitual en procesamiento y anlisis de imgenes.

Ambos filtros son separables. Si la mscara es de nxn, pasamos de o(n2) a o(2n).


Ejemplo 1. Proteccin de testigos.

Ejemplo 2. Resaltar objetos de inters.

Se aplica un suavizado pero slo en cierta regin de inters (ROI), en

este caso elptica.

Cmo encontrar la posicin de la cara

Ejemplo 2. Resaltar objetos de inters.

Se suaviza el fondo para destacar al

personaje, simulando un desenfoque.

posicin de la cara automticamente?

+

3.2.1. Operadores de suavizado. Ejemplo 2b. Simulacin de efecto tilt-shift.

La imagen parece enfocada en una zona pequea, simulando un

efecto de miniatura.

3.2.1. Operadores de suavizado. Ejemplo 3. Sombra difusa.

Aadir a una imagen A una etiqueta de texto B, con un efecto de sombra difuminada.

UBUmbralizar B, con nivel 10

Suavizado gaussiano de Desplazar S en 7 pxeles

DS

Suavizado gaussiano de 15x15, de U

Desplazar S en 7 pxeles en X e Y, y dividir por 2

Sumar U y DM


A B

Multiplicar A por M, en Sumar T y B, en posicin

M

R

Multiplicar A por M, en posicin (x0, y0)

Sumar T y B, en posicin (x0, y0)

T

3.2.2. Operadores de bordes. Perfilado y deteccin de bordes estn relacionados

con el suavizado: Suavizado: reducir las variaciones en la imagen. Perfilado: aumentar las variaciones en la imagen. Bordes: encontrar las zonas de variacin.

2

5

5 Perfil de la img.Perfil de una fila de una imagen

V

a

l

o

r

d

e

p

x

e

l

0 640320160 480

0

2

5

5

1

2

8

6

4

1

9

2

X

Perfil de la img.

Suavizado

Perfilado

Bordes

+

3.2.2. Operadores de bordes.

Matemticamente, la variacin de una funcin f(x)cualquiera viene dada por la derivada de esa funcin: f(x) > 0 : funcin creciente en X f(x) < 0 : funcin decreciente en X f(x) = 0 : funcin uniforme en X

En nuestro caso, tenemos funciones discretas. La derivada discreta se obtiene calculando diferencias.derivada discreta se obtiene calculando diferencias.

-1 10 421 3

0

2

5

5

1

2

8

6

4

1

9

2

65

V

a

l

o

r

d

e

p

x

e

l

X

f(x) = f/x

fx

x = 1f = f(x)-f(x-1)f(x) = f(x) - f(x-1)f(x)

f(x) Conclusin: la derivada se calcular con mscaras del tipo:


Mscara de derivada en X (M):

-1 1

Derivada en Y:

-11

Derivadas en diagonales:

-1 00 1

0 -11 0

Ejemplo. Derivada en X. R:= MA

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

D

e

r

i

v

a

d

a

e

n

X

(

x

2

)A R

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

D

e

r

i

v

a

d

a

e

n

X

(

x

2

)A R

[0..255]-[0..255]= [-255..255]

3.2.2. Operadores de bordes. Los bordes decrecientes se saturan a 0... Podemos sumar 128 para apreciar mejor el resultado:

Gris (128): diferencia 0 Negro: decreciente Blanco: creciente

D

e

r

i

v

a

d

a

X

(

+

1

2

8

)

D

e

r

i

v

a

d

a

Y

(

+

1

2

8

)Rx Ry

D

e

r

i

v

a

d

a

X

(

+

1

2

8

)

D

e

r

i

v

a

d

a

Y

(

+

1

2

8

)

Se produce una especie de bajorrelieve (emboss), que puede usarse en efectos especiales.

3.2.2. Operadores de bordes. Los operadores de bordes son muy sensibles al ruido. Es posible (y adecuado) combinar los operadores de

bordes con suavizados.

=1 2 12 4 21 2 1

-1 11 1 -1 -12 2 -2 -21 1 -1 -1

D

e

r

i

v

a

d

a

X

(

+

1

2

8

)Rx Rx

S

u

a

v

i

z

.

+

D

e

r

i

v

.

X


Existen algunos operadores de bordes estndar. Filtros de Prewitt:

-1 0 1-1 0 1-1 0 1

-1 -1 -10 0 01 1 1

Filtro de Prewitt 3x3,

derivada en X

Filtro de Prewitt 3x3,

derivada en Y

Filtros de Scharr:

Filtro de Scharr 3x3,

derivada en X

Filtro de Scharr 3x3,

derivada en Y

-3 0 3-10 0 10-3 0 3

-3 -10 -30 0 03 10 3


Filtros de Sobel: se construyen usando la derivada de la gaussiana.

-1 0 1-2 0 2-1 0 1

-1 -2 -10 0 01 2 1

Filtro de Sobel 3x3,

derivada en X

Filtro de Sobel 3x3,

derivada en Y-1 0 1

Adems, el filtro de Sobel permite calcular derivadas conjuntas en X e Y, derivadas segundas, terceras, etc.

Ejemplo. Derivada segunda en X.-1 1 -1 1 -1 2 -1 =

3.2.2. Operadores de bordes. Ejemplos.

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

P

r

e

w

i

t

t

Y

(

3

x

3

)

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

S

o

b

e

l

Y

(

3

x

3

)

S

o

b

e

l

2

d

e

r

i

v

.

Y


Realmente, en dos o ms dimensiones, en lugar de la derivada tiene ms sentido el concepto de gradiente.

Qu es el gradiente? Repasar clculo... El gradiente indica la direccin de mxima variacin

de una funcin (en 2D, la mxima pendiente).


El gradiente en un punto es un vector (u, v): ngulo: direccin de mxima variacin. Magnitud: intensidad de la variacin.

(u, v)dy

El gradiente est relacionado con las derivadas: u = Derivada en X del punto v = Derivada en Y del punto Teniendo dy y dx, cunto vale el ngulo y la magnitud?

dx


Clculo del gradiente: Calcular derivada en X: Dx (por ejemplo, con un filtro

de Sobel, Prewitt,...) Calcular derivada en Y: Dy Magnitud del gradiente: Dx2 + Dy2 ngulo del gradiente: atan2 (Dy, Dx)

Valor absoluto de derivada en X (Sobel de 3x3)

Valor absoluto de derivada en Y (Sobel de 3x3) Magnitud del gradiente

3.2.2. Operadores de bordes. El gradiente da lugar al concepto de borde. Un borde en una imagen es una curva a lo largo de la

cual el gradiente es mximo.

El borde es perpendicular a la direccin del

gradiente.

3.2.2. Operadores de bordes. Los bordes de una escena son invariantes a cambios de

luminosidad, color de la fuente de luz, etc. En anlisis de imgenes usar los bordes (en lugar de las originales).


Otras formas de calcular los bordes:1. Calcular la derivada en diferentes direcciones: D1, D2, D3, D4.2. Para cada punto, la magnitud del gradiente es la derivada de

mximo valor absoluto:G(x,y):= max {|D1(x,y)|, |D2(x,y)|, |D3(x,y)|, |D4(x,y)|}

3. La direccin del gradiente viene dada por el ngulo que ha producido el mximo:producido el mximo:A(x,y):= argmax {|D1(x,y)|, |D2(x,y)|, |D3(x,y)|, |D4(x,y)|}

-1 0 1-1 0 1-1 0 1

-1 -1 -10 0 01 1 1

-1 -1 0-1 0 10 1 1

0 1 1-1 0 1-1 -1 0

D1: N-S D2: NE-SO D3: E-O D4: SE-NO


Otra forma ms sencilla (aproximada) es usar mscaras de convolucin adecuadas, por ejemplo de Laplace.

La funcin de Laplace es la segunda derivada de la gaussiana.

Msc. GaussianaOperador de

suavizado

f(x) = e -x2/s2 df(x)/dxMsc. SobelOperador de derivacin

Msc. LaplacianaOperador de

gradiente

d2f(x)/dx2

3.2.2. Operadores de bordes. La mscara laplaciana se define usando la funcin de

Laplace. Ejemplos de mscaras de Laplace.

0 1 01 -4 10 1 0

-1 -1 -1-1 8 -1-1 -1 -1

Diferencia entre el pxel central y la

media de sus vecinos... 0 1 0 -1 -1 -1 vecinos...

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

L

a

p

l

a

c

i

a

n

a

2

(

3

x

3

)

3.2.2. Operadores de bordes. Detector de bordes de Canny:

No slo usa convoluciones (operadores de gradiente), sino que busca el mximo gradiente a lo largo de un borde.

El resultado es una imagen binaria (borde/no borde), ajustable mediante un umbral.

3.2.3. Operadores de perfilado.

Perfilado: destacar y hacer ms visibles las variaciones y bordes de la imagen. Es lo contrario al suavizado.

Permite eliminar la apariencia borrosa de las imgenes, debida a imperfecciones en las lentes.

... aunque tampoco se pueden hacer milagros...

Original Suavizado Perfilado

3.2.3. Operadores de perfilado. El perfilado se puede conseguir sumando a la imagen

original, la laplaciana ponderada por cierto factor. Lo cual equivale a usar una mscara de convolucin

adecuada:

-1 -1 -1-1 8 -1

0 0 00 1 0+ =

-1 -1 -1-1 9 -1

Laplaciana Identidad Perfilado

1 -1 8 -1-1 -1 -1

0 1 00 0 0

+ = -1 9 -1-1 -1 -1

0 -1 0-1 4 -10 -1 0

0 0 00 1 00 0 0

+ =

0 -a 0-a 4a+1 -a0 -a 0

a

Ms o menos perfilado dando distintos pesos, a.

1

Ojo: la funcin cvLaplace usa mscaras invertidas, luego a debe ser < 0

3.2.3. Operadores de perfilado. Ejemplos. Variando pesos y tamao de la laplaciana.

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

P

e

r

f

i

l

a

d

o

3

3

%

,

3

x

3

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

P

e

r

f

i

l

a

d

o

3

3

%

,

3

x

3

P

e

r

f

i

l

a

d

o

6

0

%

,

1

x

1

P

e

r

f

i

l

a

d

o

1

5

%

,

7

x

7

3.2.3. Operadores de perfilado. Cuidado con el perfilado. La operacin de perfilado

aumenta el nivel de ruido de la imagen.

I

m

a

g

e

n

c

o

n

r

u

i

d

o

p

o

r

i

n

t

e

r

f

e

r

e

n

c

i

a

s

T

V

P

e

r

f

i

l

a

d

o

3

3

%

,

3

x

3

I

m

a

g

e

n

c

o

n

r

u

i

d

o

p

o

r

i

n

t

e

r

f

e

r

e

n

c

i

a

s

P

e

r

f

i

l

a

d

o

3

3

%

,

3

x

3

I

m

a

g

e

n

c

o

n

r

u

i

d

o

p

o

r

c

o

m

p

r

e

s

i

n

J

P

E

G

P

e

r

f

i

l

a

d

o

6

0

%

,

3

x

3

3.2. Suavizado, perfilado y bordes.

Conclusiones: Las convoluciones son una herramienta fundamental en

procesamiento de imgenes. Una misma base comn: combinaciones lineales de una

vecindad local de los pxeles (de cierto tamao). Diversos usos: segn los valores de los coeficientes:

suavizado, eliminacin de ruido, bordes, perfilado, etc.suavizado, eliminacin de ruido, bordes, perfilado, etc. Se pueden definir operaciones similares sobre vdeo

(usando la dimensin temporal, por ejemplo, suavizado a lo largo del tiempo), y sobre audio digital (por ejemplo, suavizado de la seal o introduccin de eco).

Es importante conocer el significado matemtico de los procesos aplicados (derivadas, gradientes, integrales,...).

3.3. Filtros no lineales.

Recordatorio: las transformaciones locales son funciones del tipo:

R(x,y):= f(A(x-k,y-k), ..., A(x,y), ..., A(x+k,y+k))

En las convoluciones, f es una combinacin linealcualquiera. Pero...cualquiera. Pero...

Tambin puede ser interesante usar otras funciones no lineales.

Ejemplo, media geomtrica.R(x,y):= A(x-1,y-1)A(x,y-1)A(x-1,y)A(x,y)4

3.3. Filtros no lineales. Ejemplo. Media geomtrica de 5x5. ... muy parecido a la

media aritmtica...

Aunque existen muchas (en teora infinitas) posibles transformaciones no lineales, en la prctica no todas son tiles e interesantes.

Las que ms se usan son: mximo, mnimo y mediana.

3.3. Filtros no lineales. Filtro de Mximo:

R(x,y):= max {A(x-k,y-k), ..., A(x,y), ..., A(x+k,y+k)}donde k es el radio, el tamao (o apertura) es 2k+1

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

M

x

i

m

o

,

t

a

m

a

o

3

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

M

x

i

m

o

,

t

a

m

a

o

3

M

x

.

,

t

a

m

a

o

6

M

x

.

,

t

a

m

a

o

1

2

3.3. Filtros no lineales. El resultado es un cierto efecto de difuminacin y

aclaramiento de la imagen. Desaparecen los detalles ms oscuros.

Si el tamao es grande, pueden ocurrir dos efectos:1. Efecto de cuadriculado.

Como el mximo se aplica enuna zona cuadrada, los pxelesmuy claros generan unmuy claros generan uncuadrado uniforme alrededor.

2. Aparicin de colores falsos.Al aplicarlo en los tres canales(R,G,B) independientemente,el mximo en los 3 puede nocorresponder a un colorpresente en la imagen original.

3.3. Filtros no lineales. Filtro de Mnimo:

R(x,y):= min {A(x-k,y-k), ..., A(x,y), ..., A(x+k,y+k)}donde k es el radio, el tamao (o apertura) es 2k+1

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

M

n

i

m

o

,

t

a

m

a

o

3

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

M

n

i

m

o

,

t

a

m

a

o

3

M

n

.

,

t

a

m

a

o

6

M

n

.

,

t

a

m

a

o

1

2

3.3. Filtros no lineales. El efecto es parecido al mximo, pero tomando los valores

menores (los ms oscuros).Mximo

Mnimo

Ideas: Para evitar el efecto de cuadriculado se podra aplicar

el mximo/mnimo a una zona circular. Para evitar la aparicin de colores falsos se podra

tomar el mximo de las sumas de R+G+B.

3.3. Filtros no lineales. Otro filtro relacionado es el de la mediana. La mediana de m nmeros es un nmero p tal que m/2

de esos nmeros son p, y otros m/2 son p.R(x,y):= mediana {A(x-k,y-k), ..., A(x,y), ..., A(x+k,y+k)}

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

M

e

d

i

a

n

a

3

x

3

I

m

a

g

e

n

d

e

e

n

t

r

a

d

a

M

e

d

i

a

n

a

3

x

3

M

e

d

i

a

n

a

6

x

6

M

e

d

i

a

n

a

1

2

x

1

2

3.3. Filtros no lineales. La mediana produce un efecto de suavizado, aunque ms

abrupto en los bordes que la media y el suavizado gaussiano.

Suavizado

Pero el verdadero inters es la eliminacin de ruido puntual.

MedianaMedianaSuavizado gaussiano


Ejemplo. El ruido denominado sal y pimienta es producido por picos de perturbacin, positivos o negativos. Puede deberse a un canal ruidoso.

3.3. Filtros no lineales. Se puede intentar eliminar (o reducir) el ruido con un filtro

gaussiano o con una mediana.

M

e

d

i

a

n

a

3

x

3

M

e

d

i

a

n

a

3

x

3

F

i

l

t

r

o

g

a

u

s

s

i

a

n

o

3.3. Filtros no lineales. Se puede intentar eliminar (o reducir) el ruido con un filtro

gaussiano o con una mediana.

M

e

d

i

a

n

a

3

x

3

Con este tipo de ruido funciona mucho mejorM

e

d

i

a

n

a

3

x

3

F

i

l

t

r

o

g

a

u

s

s

i

a

n

o

El ruido se difumina, pero no

llega a desaparecer

mucho mejor

3.3. Filtros no lineales. Otros ejemplos de eliminacin de ruido.

M

e

d

i

a

n

a

7

x

7

M

e

d

i

a

n

a

7

x

3


Ms filtros no lineales: recordar la ecualizacin local del histograma. Considerar una operacin global como el estiramiento,

la ecualizacin del histograma o la umbralizacin. Globalmente se calculan los parmetros y se aplican a

toda la imagen: estiramiento (mximo y mnimo del histograma), ecualizacin (funcin de ecualizacin) y histograma), ecualizacin (funcin de ecualizacin) y umbralizacin (umbral a aplicar).

En lugar de aplicarlos globalmente, calcular los parmetros para cada punto, usando una vecindad local.

Aplicar la transformacin a cada punto, usando sus parmetros especficos.


Algoritmo. Ecualizacin local de tamao axb:1. Para cada punto (x,y) de la imagen A, calcular el

histograma de una regin rectangular desde(x-a, y-b) hasta (x+a, y+b) H(v)

2. Calcular el percentil del valor A(x,y), es decir:p:= (H(0)+H(1)+...H(A(x,y)))/((2a+1)(2b+1))

3. Hacer R(x,y):= 255p3. Hacer R(x,y):= 255p

62%

0,62*255 = 158

3.3. Filtros no lineales. Ejemplo. Ecualizacin local del histograma.

Imagen de entradaResolucin: 299x202

Tamao: 25x25 Tamao: 50x50 Tamao: 120x120 La misma idea se podra aplicar a umbralizacin y

estiramiento.

3.4. Morfologa matemtica.

Los operadores de morfologa matemtica son un conjunto de filtros locales sencillos, que se pueden combinar para obtener resultados ms complejos.

Originalmente, estn definidos sobre imgenes binarias.

La idea es muy parecida a una convolucin, pero utilizando las operaciones booleanas AND y OR.utilizando las operaciones booleanas AND y OR.

Ejemplo. R(x,y):= A(x-1,y-1) AND A(x,y) AND A(x+1,y+1)

1 0 00 1 00 0 1

Elemento estructurante(= mscara de convolucin)

(x-1,y-1)

(x+1,y+1)

(x,y) Punto de ancla

3.4. Morfologa matemtica. El elemento estructurante define los pxeles que se usan en

la operacin (1s) y los que no (0s). Dado un elemento estructurante, E, de cierta forma y tamao,

y una imagen binaria B, se definen dos operaciones: Dilatacin BE. Aplicar la operacin OR a los pxeles

correspondientes a 1 en el elemento estructurante. El resultado es 1 si al menos una operacin es 1

Erosin B E. Aplicar la operacin AND a los pxeles correspondientes a 1 del elemento estructurante.

El resultado es 1 si todas las operaciones son 1 La idea se puede generalizar a imgenes no binarias:

Dilatacin. Operar con Mximo. Erosin. Operar con Mnimo.


Dilatacin ABDilatacin AB

Erosin

3.4. Morfologa matemtica. El efecto de la dilatacin es extender o ampliar las

regiones de la imagen con valor 1 (color blanco), mientras que la erosin las reduce.

La cantidad depende del tamao y forma del elemento estructurante y del nmero de veces que se aplican.

Ejemplo.Imagen de entrada

D

i

l

a

t

a

c

i

n

1

D

i

l

a

t

a

c

i

n

3

Elemento estructurante

1 1 11 1 11 1 1

D

i

l

a

t

a

c

i

n

1

D

i

l

a

t

a

c

i

n

3

E

r

o

s

i

n

1

E

r

o

s

i

n

3


Existen otras dos operaciones frecuentes basadas en erosin y dilatacin: Abrir. Aplicar erosin y despus dilatacin: (B E)E Cerrar. Aplicar dilatacin y despus erosin: (BE ) E

Imagen de entradaAbrir:desaparecen los puntos sueltos o

Elemento estructurante

1 1 11 1 11 1 1

puntos sueltos o estructuras finas

Cerrar: se rellenan los huecos negros de cierto tamao


Ejemplo. Segmentacin de objetos.Para segmentar un objeto del fondo usamos una simple umbralizacin. Funciona ms o menos bien, pero aparecen algunos puntos mal clasificados.

Imagen de entrada Umbralizada (u=130)

Falsos negativos

Falsos positivos

Usar morfologa para arreglar los falsos.

3.4. Morfologa matemtica.Cerrar 2 (BEE) E EImagen umbralizada

E

l

i

m

i

n

a

r

f

a

l

s

o

s

n

e

g

a

t

i

v

o

s

Abrir 1 (B E)EE

l

i

m

i

n

a

r

f

a

l

s

o

s

p

o

s

i

t

i

v

o

s

Erosin 2 (B E) E

E

l

i

m

i

n

a

r

p

x

e

l

e

s

d

e

l

o

s

b

o

r

d

e

s

Dilatacin BE

Erosin B E

Abrir. Aplicar erosin y despus dilatacin: (B E)E

3.4. Morfologa matemtica. En imgenes no binarias, el resultado de dilatacin y

erosin es parecido a las operaciones de mximo y mnimo. De hecho, es igual si el elemento estructurante es todo 1.

I

m

a

g

e

n

e

n

t

r

a

d

a

E

r

o

s

i

n

,

1

I

m

a

g

e

n

e

n

t

r

a

d

a

E

r

o

s

i

n

,

1

D

i

l

a

t

a

c

i

n

,

3

C

i

e

r

r

e

,

2

EjemplosUna imagen binaria contiene una mezcla de crculos y lneas. Suponga que se quieren separar los crculos, para contarlos. Aplicando la abertura con una forma de disco con 11 pixeles de dimetro se obtiene

Algunos crculos aparecen distorsionados pero Algunos crculos aparecen distorsionados pero en general las lineas se han eliminado.

Apertura con elementro estructurante 39

Apertura con elementro estructurante 93

CerrarUna imagen contiene regiones circulares grandes y pequeas. Remover las pequeas y dejar las grandes

Cerrar con un un elemento estructurante cirucular de diametro mayor que el pequeo y menor que el mayor.pequeo y menor que el mayor.

Resultado de la cerrar con un disco de diametro de 22 pixeles.

3.4. Morfologa matemtica. Existen otras operaciones de morfologa, basadas en

las elementales, que son tiles en anlisis de imgenes. Ejemplo 1. Borde morfolgico: (BE) - B

Imagen de entrada Borde morfolgico

Ejemplo 2. Adelgazamiento (thinning). Aplicar una erosin, pero no eliminar el punto (no poner a 0) si se separa una regin conexa en varias o si slo queda un punto.

Ejercicio

1 1 0 1 1 1

0 1 1 0 0 0

0 0 1 1 1 0

0 0 0 1 1 11 1 1

Dada la imagen A y el elemento estructurante B hacer las siguientes operaciones:

a)Dilatacin, b) Erosin, c) Apertura y d) Cierre

A=

B=0 0 0 1 1 1

0 0 0 0 1 1

1 1 1B=

3. Filtros y transformaciones locales.

Conclusiones: Las operaciones de procesamiento local son esenciales

en mejora de imgenes, restauracin, anlisis, etc. Dos categoras bsicas:

Filtros lineales o convoluciones: la salida es una combinacin lineal de los pxeles en una vecindad Suavizado, bordes, perfilado, etc.Suavizado, bordes, perfilado, etc.

Filtros no lineales: se usan funciones no lineales Mximo, mnimo, operaciones de morfologa, etc.

Es posible combinarlas con operaciones de procesamiento global.

La idea de localidad se puede extender a vdeo y a sonido, considerando la dimensin temporal.

Apndice: Lgica de conjuntos A es un conjunto en Z2 , a=(a1,a2) es un elemento de A, aA. Si no, entonces aA : conjunto nulo (vacio) Un subconjunto de B: AB Un subconjunto de B: AB Union de A y B: C=AB Interseccin de A y B: D=AB Conjunto disjunto: AB= Complemento de A: Ac = {x|xA} Diferencia de A y B:

A-B = {x|xA, x B} = ABc

Operaciones Lgicas en imgenes Binariaspppp qqqq p AND qp AND qp AND qp AND q p OR qp OR qp OR qp OR q NOT pNOT pNOT pNOT p

0000 0000 0000 0000 1111

0000 1111 0000 1111 1111

1111 0000 0000 1111 00001111 0000 0000 1111 0000

1111 1111 1111 1111 0000

3 Filtros Covolucion y Morfologia

Documents

Transcript of 3 Filtros Covolucion y Morfologia