1

UNIDAD 8:

GEOMETRÍA PLANA

3º ESO MATEMÁTICAS APLICADAS

2

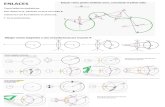
1. Lugares geométricos

1.1. La circunferencia

1.2. Mediatriz de un segmento

1.3. Bisectriz de un ángulo

2. Elementos notables de un triángulo

3. Ángulos, Longitudes y áreas.

3.1. Teorema de Pitágoras

3.2. Ángulos de un polígono

3.2.1. Suma de los ángulos interiores de un polígono

3.2.2. Cálculo de un ángulo interior de un polígono regular

3.3. Longitudes y áreas de figuras poligonales

3.4. Longitudes y áreas de figuras circulares

4. Semejanza de figuras.

4.1. Figuras semejantes

4.2. Triángulos semejantes. Criterios de semejanza.

4.3. Teorema de Thales. Triángulos en posición de Thales.

3

1. Lugares geométricos

A menudo, definimos una figura geométrica como los puntos del plano que verifican alguna condición. Decimos entonces que dicha figura es un lugar geométrico del plano. Veamos algunos ejemplos que ya conoces:

1.1. La circunferencia

Una circunferencia es el lugar geométrico de los puntos del plano cuya

distancia a un punto de dicho plano, que llamamos centro, O, siempre es

constante. A esa cantidad constante se le llama radio, r.

Esto quiere decir que todo punto P del plano que esté a una distancia r del

centro O está en la circunferencia.

1.2. Mediatriz de un segmento

La mediatriz de un segmento AB es el lugar geométrico de los puntos del plano que equidistan de los extremos A y B. Es decir, todo punto P del plano que esté a la misma distancia de A y de B está en la mediatriz del segmento AB.

4

1.3. Bisectriz de un ángulo

Consideramos un ángulo � delimitado por dos rectas, la bisectriz de � es el lugar geométrico de los puntos del plano que equidistan de dichas rectas.

Todo punto P que esté a la misma distancia de las rectas que forman el ángulo �, está en la bisectriz. Observemos que la bisectriz pasa por el vértice del ángulo � y lo divide en dos ángulos iguales.

Ejercicio 1: Un agricultor encuentra en su campo una bomba de la guerra Civil. Para acordonar la zona, la Guardia Civil debe establecer un perímetro de seguridad de 50 metros. ¿Cómo deben hacerlo? Dibújalo.

Ejercicio 2: Cuando en una acampada se sientan alrededor del fuego lo hacen formando un círculo, ¿por qué?

Ejercicio 3: Un juego de dos participantes consiste en que se sitúan a una distancia de dos metros entre sí y se ponen varias banderas a la misma distancia de ambos. La primera a 5 metros, la segunda a 10 metros, la tercera a 15 y así sucesivamente. ¿Sobre qué línea imaginaria están situadas las banderas?

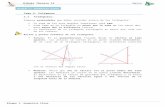
2. Elementos notables de un triángulo

2.1. Mediatrices

Las mediatrices de un triángulo son rectas perpendiculares a cada uno de los lados del triángulo en su punto medio.

5

Las tres mediatrices se cortan en un punto, O, llamado circuncentro. Ese circuncentro es el centro de una circunferencia que pasa por los tres vértices del triángulo y se llama circunferencia circunscrita.

Si la mediatriz de un segmento es el lugar geométrico de los puntos que equidistan de los extremos del segmento, cada mediatriz del triángulo equidistará de dos de los vértices del triángulo.

2.2. Bisectrices

Las bisectrices de un triángulo son las rectas que dividen al ángulo en su

mitad

Un triángulo tiene 3 bisectrices.

El punto O donde concurren las tres bisectrices se llama incentro. El incentro

corresponde al centro de una circunferencia interior del triángulo, que se llama

circunferencia inscrita.

6

Si la bisectriz de un ángulo equidista de los lados del ángulo, cada una de las

tres bisectrices del triángulo equidistará de dos de los lados del triángulo.

El incentro, que es el punto donde se cortan las tres bisectrices del triángulo,

equidistará de dos de los tres lados del triángulo.

2.3. Alturas

Las alturas de un triángulo son segmentos perpendiculares (segmentos que

forman ángulos de 90º) a un lado o a su prolongación desde el vértice opuesto.

La altura se designa con la letra h y un subíndice que señala el lado del cual se

levanta.

Un triángulo tiene tres alturas, una por cada lado .hA, hB y hC

El punto O donde concurren las tres alturas se llama Ortocentro (H).

El lado y su altura forman un ángulo de 90º.

2.4. Medianas

Las medianas de un triángulo son los segmentos que unen directamente los

puntos medios de dos lados del triángulo, de dos en dos. Pasan por un vértice

y el punto medio del lado opuesto, dividiendo al triángulo en dos mitades

7

iguales. Las designamos con la letra m y un subíndice que indica el lado sobre

el cual se proyecta., mA, mB y mC.

Las medianas del triángulo se cortan en un punto M llamado baricentro.

Propiedades del baricentro:

1) El baricentro verifica que la distancia del baricentro a cada lado es el doble

de su distancia al vértice opuesto correspondiente, es decir, en cualquier

mediana, la distancia entre el baricentro M y el centro de su lado

correspondiente es 1/3 de la longitud de dicha mediana.

2) Una mediana divide al triángulo en dos triángulos de igual área.

En efecto, los dos triángulos Δ ABP y Δ PBC

tienen igual base. AP = PC, por la misma

definición de la mediana, y la misma altura h

referida a esa recta de las dos bases desde el

vértice B.

3).En Física, el baricentro sería el centro de gravedad del triángulo, es decir, si

construimos un triángulo de papel y dibujamos su baricentro, al poner el

triángulo horizontalmente en el aire solo sujetado por la punta de un lápiz en el

baricentro, se sujeta. Puedes comprobarlo.

8

4). El baricentro está siempre en el interior del triángulo.

Nota 1: En cualquier triángulo el circuncentro, el ortocentro y el baricentro están

sobre una misma recta, llamada Recta de Euler.

Nota 2: A las mediatrices, bisectrices, alturas y medianas de un triángulo se les

llama rectas notables.

Ejercicio 4: Dibuja en tu cuaderno un triángulo de lados 7, 6 y 4 cm. Traza

en él las circunferencias inscritas y circunscritas.

Ejercicio 5: Dibuja en tu cuaderno un triángulo de lado 8 cm y ángulos

adyacentes al mismo de 40º y 30º. Encuentra su ortocentro y baricentro.

Ejercicio 6: Dibuja en tu cuaderno un triángulo con un ángulo de 40º

comprendido entre dos lados de 6 y 4 cm. Obtén su circuncentro y su

incentro.

Ejercicio 7: ¿Qué pasa con las rectas y los puntos notables de un triángulo

equilátero?

Ejercicio 8: Dibuja un triángulo isósceles con el ángulo desigual de 40º y

30º. Traza las rectas notables para el lado desigual y para uno de los lados

iguales. ¿Qué pasa?

Ejercicio 9: Una hormiga anda por una mediana de un triángulo partiendo

del vértice. Cuando llega al baricentro ha recorrido 8 cm. ¿Qué distancia le

falta para llegar al punto medio del lado opuesto al vértice de donde

partió?

9

Ejercicio 10: Queremos situar una farola en una plaza triangular. ¿Dónde la

pondríamos?

Ejercicio 11: Tenemos un campo triangular sin cerrar y queremos atar una

cabra de forma que no se salga del campo pero que acceda al máximo de

pasto posible. ¿Dónde pondríamos el poste?

Ejercicio 12: La madre de Nicolás y Emma ha hecho una tarta triangular

solo para los dos. Por sorteo, Nicolás elige el primer trozo pero Emma ha

sido la elegida para cortar la tarta. ¿Cómo debe hacerlo para comer tanto

como su hermano?

Ejercicio 13: ¿Dónde está el ortocentro de un triángulo rectángulo?

Ejercicio 14: Comprueba que el circuncentro de un triángulo rectángulo está

siempre en el punto medio de la hipotenusa.

Ejercicio 15: Calcula el lado de un triángulo equilátero inscrito en una

circunferencia de 10 cm de radio. Ayuda: Aplica que en este caso el

circuncentro coincidecon el baricentro y que éste último está al doble de

distancia del vértice que del lado opuesto.

3. Ángulos, Longitudes y áreas.

3.1. Teorema de Pitágoras

Teorema de Pitágoras: En un triángulo rectángulo con catetos � � �, e hipotenusa, a, se verifica que la hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos.

Matemáticamente,

10

�� �� c�

Demostración geométrica:

Aplicaciones del Teorema de Pitágoras:

1. Conociendo los dos catetos de un triángulo rectángulo, podemos obtener la

hipotenusa: h ��� ��

�

Ejemplo 1: Si los catetos de un triángulo rectángulo miden 10 cm y 24 cm, ¿cuánto mide su hipotenusa?

Es decir, la hipotenusa mide 26 cm.

2. Conociendo un cateto y la hipotenusa de un triángulo rectángulo, podemos obtener el otro cateto, por ejemplo el ��:

ℎ� ��� ��

� → ��� ℎ����

� → �� ℎ� � ���

Ejemplo 2: Si tenemos un triángulo rectángulo cuya hipotenusa mide 26 cm y un cateto mide 24 cm, ¿cuánto mide el otro?

11

26� 24� ��� → ��

� 26� � 24� → ��� 676 � 576 100 → �� √100

10

Es decir, el otro cateto mide 10 cm.

Ejercicio 16: ¿Es posible encontrar un triángulo rectángulo cuyos catetos midan 5 y 12 cm y su hipotenusa 24 cm? Si tu respuesta es negativa, halla la medida de la hipotenusa de un triángulo rectángulo cuyos catetos miden 5 cm y 12 cm.

Ejercicio 17: Calcula la longitud de la hipotenusa de los siguientes triángulos rectángulos de catetos: a) 6 cm y 8 cm c) 8 dm y 15 dm b) 4 m y 3 m d) 13,6 km y 21,4 km

Ejercicio 18: Calcula la longitud del cateto que falta en los siguientes triángulos rectángulos de hipotenusa: a) 17 m y 8 m b) 37 dm y 35 dm c) 14,7 km y 5,9 km

Ejercicio 19: Calcula las dimensiones de la figura:

Ejercicio 20: Calcula la longitud de la diagonal de un rectángulo de base 15 cm y altura 8 cm.

12

Ejercicio 21: Una portería de futbol mide 7,32m de ancho por 2,44 m de alto. El punto de penalti está a 10 metros. Calcula la distancia que recorre el balón en: a) Un tiro directo a la base del poste b) Un tiro directo a la escuadra

Ejercicio 22: Demuestra que el diámetro de un cuadrado de lado x es � √2�

Ejercicio 23: Demuestra que la altura de un triángulo equilátero de lado x es

� √��

�

3.2. Ángulos de un polígono

3.2.1. Suma de los ángulos interiores de un polígono

Triángulos: La suma de los ángulos interiores de un triángulo de ángulos A, B y C es 180º.

Demostración gráfica:

13

Polígonos regulares de n lados donde n=4, 5, 6, …

Por ejemplo,

3.2.2. Cálculo de un ángulo interior de un polígono regular

Si el polígono de n lados es regular (es decir, todos los lados y todos los ángulos son iguales) podemos calcular un ángulo interior dividiendo entre n la suma de los ángulos interiores.

Ejemplo: Pentágono regular

Ejercicio 24: Calcula los ángulos central e interior del triángulo equilátero,

cuadrado, pentágono regular, hexágono regular y eneágono regular.

14

Ejercicio 25: Justifica que un hexágono regular se puede descomponer en 6 triángulos equiláteros.

Ejercicio 26: Dos ángulos de un triángulo isósceles miden 35º y 72º, ¿cuánto mide el ángulo que falta?

Ejercicio 27: ¿Cuánto mide la suma de los ángulos interiores de un decágono regular?

3.3. Longitudes y áreas de figuras poligonales

Recordemos:

Recordemos también los tipos de trapecios que conocemos:

Trapecio rectángulo: Tiene un ángulo recto (es decir, un lado es perpendicular a su base)

15

Trapecio isósceles: Tiene dos lados no paralelos de igual medida. Tiene dos ángulos internos agudos y dos obtusos, que son iguales entre sí.

Trapecio escaleno: No es isósceles ni rectángulo. Todos sus lados son diferentes.

Ejercicio 28: Calcula el área de un triángulo equilátero de lado 9.

Ejercicio 29: Calcula el área de un hexágono regular de lado 2 cm.

Ejercicio 30: Calcula el área y el perímetro de un trapecio isósceles de bases 50 cm y 26 cm y altura 5 cm.

Ejercicio 31: Calcula el área y el perímetro de un trapecio rectángulo de bases 100 cm y 64 cm y altura 77 cm.

Ejercicio 32: Calcula el área y el perímetro de un trapecio isósceles de bases 100 cm y 64 cm y lados laterales 29 cm.

Ejercicio 33: Teniendo en cuenta que un hexágono regular se puede dividir en seis triángulos equiláteros (cuya altura es la apotema del hexágono regular), calcula el área de un hexágono regular de 5cm de lado.

16

3.4. Longitudes y áreas de figuras circulares

Ejemplos:

1. La circunferencia de radio 5 cm tiene una longitud � 2�� 2 � 5

10� 31,416 �#.

2. Las ruedas de un carro miden 60 cm de diámetro y tienen 16 radios. La

longitud del arco de cada radio es: (si hay 16 radios, el ángulo nº=�%&�%

22,5º y

el radio es %&�

30 �#(

� 2��)º

360

2� 30 22.5360

11,78 �#

3. El área de un círculo de radio 8 cm es + 64� 201,06 �#�

4. El área de un círculo de radio 10 cm es + 100� 314,16 �#�

17

5. El área de un círculo de diámetro 10 cm es + 25� 78,54 �#� pues el diámetro es el doble del radio.

6. El área de la corona circular formada por las circunferencias concéntricas de radios 9 cm y 5 cm es igual a:

+ � ,-� � ��( � ,9� � 5�( ,81 � 25( � 56� 175,93 �#�

7. Para hallar el área del sector circular de radio 10 m que abarca un ángulo de 90º,

Primero: Calculamos el área del círculo completo:

+ � -� � 10� 100� 314 #�

Segundo: Hallamos la proporción del círculo del que queremos encontrar su área, en este caso:

360º – 100� #�� � 90 100�

360 78,54 #�

90º – � #�

Ejercicio 34: La menor de las circunferencias de la diana tiene como radio 1 cm, la siguiente, 2 cm, aumentando el radio de cada circunferencia de 1 cm en 1 cm. Calcula las longitudes de todas las circunferencias de la diana.

Ejercicio 35: La Tierra es aproximadamente una esfera de radio 6379 km, ¿Cuánto mide el ecuador?

Ejercicio 36: Un faro gira describiendo un arco de 170º. A una distancia de 5 km, ¿Cuál es la longitud del arco de circunferencia en el que se ve la luz?

18

Ejercicio 37: Determina el área del triángulo equilátero de radio 9cm.

Ejercicio 38: Calcula el área de la corona circular de radios 12 y 5 cm.

Ejercicio 39: Calcula el área del sector circular y del segmento circular de radio 6 cm y que forma un ángulo de 60º.

Ejercicio 40: Calcula el área del sector de corona circular de radios 25 cm y 18 cm y que forma un ángulo de 60º.

Ejercicio 41: Calcula el área encerrada entre estos círculos de 5 cm de radio.

Ejercicio 42: Queremos construir una rotonda para una carretera de 9 metros de ancho de forma que el círculo interior de la rotonda tenga la misma área que la corona circular que forma la carretera. ¿Qué radio debe tener la rotonda?

19

4. Semejanza de figuras.

4.1. Figuras semejantes

Dos figuras semejantes tienen la misma forma. Es muy útil saber reconocer la semejanza para poder estudiar una figura y deducir así propiedades de una figura semejante a ella que es más grande o inaccesible. La semejanza conserva ángulos y mantiene la proporción entre las distancias.

Dos polígonos son semejantes si sus lados son proporcionales y sus ángulos son iguales.

4.2. Triángulos semejantes. Criterios de semejanza.

Dos triángulos son semejantes si tienen todos los ángulos iguales y los lados proporcionales.

Para reconocer dos triángulos semejantes no es necesario conocer todos los lados y ángulos, basta con que cumplan alguno de los siguientes criterios de semejanza.

20

• Primer criterio de semejanza: Dos triángulos son semejantes sí tienen dos ángulos iguales. Ejemplo:

• Segundo criterio de semejanza: Dos triángulos son semejantes sí tienen los tres lados proporcionales.

Ejemplo:

• Tercer criterio de semejanza: Dos triángulos son semejantes si tienen dos

lados proporcionales y el ángulo que forman es igual.

Ejemplo:

21

Ejercicio 43: Indica si son semejantes los siguientes pares de triángulos: a) Un ángulo de 80º y otro de 40º. Un ángulo de 80º y otro de 60º. b) Triángulo isósceles con ángulo desigual de 70º. Triángulo isósceles con ángulo igual de 50º. c) A=30º, b=7 cm, c=9 cm. A’=30º, b’=3,5 cm, c’=4,5 cm. d) a=4 cm, b=5cm, c=7 cm, a’=10 cm, b’=12,5 cm, c’=24,5 cm.

Ejercicio 44: Calcula el valor desconocido para que los triángulos sean semejantes: a=9 cm, b=6 cm, c=12 cm, a’=6 cm, b’=4 cm, ¿ c’= ?

Ejercicio 45: Un triángulo tiene lados de 6 cm, 7 cm y 7 cm. Un triángulo semejante a él tiene un perímetro de 60 cm. ¿Cuánto miden sus lados?

4.3. Teorema de Thales. Triángulos en posición de Thales.

Dos triángulos están en posición de Thales cuando dos de los lados de cada uno están sobre las mismas rectas y los otros lados son paralelos.

Los ángulos son iguales. Uno porque es el mismo, los otros dos por estar formados por rectas paralelas. Por lo tanto, por el primer criterio de semejanza de triángulos, los triángulos son proporcionales y se cumple:

+′1′+1

1′2′12

+′2′+2

22

Teorema de Thales: Sirve para establecer una relación

entre los segmentos formados cuando dos rectas

cualesquiera son cortadas por varias paralelas.

En esta figura, podemos apreciar cómo se forman en

este caso tres triángulos semejantes y por lo tanto

podemos establecer que:

+′1′+1

1′2′12

+′2′+2

Observación: En este caso no relacionamos los segmentos AA’, BB’ y CC’ que

se forman sobre los lados paralelos.

23

Ejercicio 46: calcula los valores de x e y en las siguientes figuras.

Ejercicio 47: Un poste muy alto se sujeta con cables de acero que van de su extremo superior al suelo. La distancia del anclaje de uno de los cables a la base del poste es 6 metros. Ponemos una barra de 120 cm de forma que está perpendicular al suelo y justo toca el suelo y el cable. Su distancia al anclaje del cable es 90 cm. Dibújalo y calcula la longitud del poste y la longitud del cable de acero.

Ejercicio 48: María mide 160 cm. Su sombra mide 90 cm. En ese mismo instante se mide la sombra de un edificio y mide 7,2 m. Dibújalo. ¿Cuánto mide el edificio?

Ejercicio 49: Calcula las longitudes que se indican: