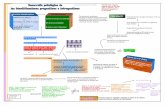
Modelo de penetración térmica Bidimensional
description
Transcript of Modelo de penetración térmica Bidimensional

APÉNDICE AMODELO DE PENETRACIÓN TÉRMICA BIDIMENSIONAL
PROBLEMA CONTINUO DE ESTIMACIÓN
Como se ha explicado en la Sección 2, el problema inverso de estimación puedeplantearse como la minización del funcional F
minimizartlRefract
F = 1
2
tT �xOBSi ; tlRefract�� tTOBSi
2 i = 1; ntc (1)
Sin embargo la nolinealidad y mal condicionamiento del problema así planteado requierela utilización de un método iterativo de regularización como el Método de Gauss-Newton,que presenta una estabilización adicional al Método de LevenbergMarquardt [8,9], teniéndosepara el primero de ellos
tlIter+1Refract =tlIterRefract
+�D
� tT�tlIterRefract
�D tT
�tlIterRefract
�+ � I
��1�hD
� tT�tlIterRefract
� �tTOBSi � tT
�tlIterRefract
��+ �
�tl4Refract � tlIterRefract
�i(2)
tlIter+1Refract =tlIterRefract + � tlIterRefract (3)
donde:
� se representa como D tT�tlIterRefract
�a las derivadas de T respecto a lRefract. Estos
operadores reciben el nombre de �operadores de sensibilidad�, y tienen la característicade ser derivadas de una función con respecto a otra función. Estas derivadas sonllamadas derivadas de Frechet, y al discretizarse el problema pasarán a ser derivadasparciales.
� tl4Refract corresponde a un valor de referencia para la variable tlRefract. Lascaracterísitcas del problema nos permiten utilizar como valor de referencia para lavariable tlRefract su valor correspondiente al instante de tiempo inmediato anteriort�1lRefract. Esto se debe a que el proceso de erosión, y en general los fenómenosque ocurren dentro del crisol del alto horno, son procesos lentos y es de esperar quela con�guración de la variable lRefract no cambie mucho entre instantes de tiemposucesivos.
� � es un parámetro de regularización y juega un rol crucial ya que representa uncompromiso entre exactitud y estabilidad: si � es muy grande se obtiene una malaaproximación a las observaciones, y si � es muy pequeño es posible que erroresexistentes en las mediciones se ampli�quen fuertemente.
28

Elección del parámetro de regularización
La elección del parámetro de regularización � puede realizarse de dos formas distintas:
� utilizando reglas �a priori� en las cuales el parámetro es función del nivel de errorde las observaciones, � = �(�), donde � llamado nivel de ruido indica una cotasuperior para la discrepancia entre las mediciones y sus valores reales TREAL � TOBS 2 � � , (4)
� utilizando reglas �a posteriori� en las cuales el parámetro es función del nivel deruido � y de las observaciones TOBS , siendo � = �(�; TOBS).
La elección �a priori� del parámetro � cuando se utiliza el Método de Regularizaciónde Tikhonov en problemas no lineales responde a [8]
� � �2
2�+1 , (5)
donde � 2 [1=2; 1]. Sin embargo en nuestro caso se ha utilizado como criterio deelección aún cuando se emplea el Método Iterativo de Regularización de Gauss-Newton,teniéndose un comportamiento satisfactorio con � = 1.
Determinación de la longitud del paso iterativo
Con respecto a la evolución del proceso iterativo se propone utilizar una subrelajaciónsobre la Ec.2 con una longitud del paso iterativo �Iter (0 < �Iter < 1), de forma tal quesiendo
tlIter+1Refract =tlIterRefract + �
Iter � tlIterRefract (6)
se adopte una longitud de paso que haga mínimo el funcional F . La determinación dela longitud de paso iterativo resulta de gran utilidad para la convergencia del algoritmoiterativo ya que los operadores de sensibilidad son evaluados en un entorno de tlIterRefract ydada la marcada nolinealidad del problema suelen resultar inexactos para un entorno detlIter+1Refract.
Generalización del Método Iterativo de Regularización de Gauss-Newton
ElMétodo Iterativo de Regularización de Gauss-Newton puede generalizarse utilizandoun operador diferencial que afecte al término de regularización [9], reescribiéndose laEc.2 como
tlIter+1Refract =tlIterRefract
+�D
� tT�tlIterRefract
�D tT
�tlIterRefract
�+ � L�L
��1�hD
� tT�tlIterRefract
� �tTOBSi � tT
�tlIterRefract
��+ � L�L
�tl4Refract � tlIterRefract
�i(7)
29

donde el operador diferencial L es, en lugar de la identidad como se utiliza en la Ec.2, unoperador de derivada primera o de derivada segunda.
En el modelo desarrollado, el operador diferencial se aproximó en forma discretautilizando una matriz de regularización que responde a la factorización
LTL =
2Xk=0
wk LTkLk , (8)
dondeL0 = I 2 Rn�n (9)
L1 =
264 1 �1. . . . . .
1 �1
375 2 R(n�1)�n (10)
L2 =
264 1 2 �1. . . . . . . . .
1 2 �1
375 2 R(n�2)�n (11)
y donde wk � 0 son factores de peso tales que2Xk=0
wk = 1. En nuestro problema se usó
w0 = 0:75 , (12)w1 = 0:00 , (13)w2 = 0:25 . (14)
Criterio de convergencia
La convergencia del algoritmo iterativo se determina según el criterio tT Iter+1 � tT Iter
k tT Iterk � TOL � �Iter
existiendo un número de iteraciones máximas permitidas. La utilización de un número deiteraciones máximas permitidas es importante en la resolución de problemas no linealesmal condicionados ya que la simple minimización del funcional planteado puede llevar asoluciones inestables o con mucho error.
30

PROBLEMA DISCRETO DE ESTIMACIÓN
Para el caso discreto, bidimensional, la parametrización de la geometría debe realizarseutilizando un conjunto de parámetros o variables escalares, tlRefract, y se tiene:
t ~T = N(x) T (15)
t ~T�tlIterRefract +�
tlRefract�= N(x) T
�tlIterRefract
�+
npXi=1
N(x)
@T�tlIterRefract
�@tl
(i)Refract
�tl(i)Refract
(16)donde N(x) y T son las funciones de forma y las temperaturas nodales asociadas a
la malla de elementos �nitos utilizada, siendo@T
�tlIterRefract
�@tl
(i)Refract
los valores nodales de
los operadores de sensibilidad discretizados en el mismo soporte de elementos �nitosutilizado para el cálculo de la función t ~T .
Por lo tanto el sistema de ecuaciones a resolver (Ec.7), para una iteración Iter delciclo iterativo, queda de�nido por
tlIter+1Refract =tlIterRefract+
�Iter�ATA+� LTL
��1 � �ATb+� LTL�tl�Refract � tlIterRefract
��(17)
donde la matrizA es función de los operadores de sensibilidad, de dimensión (ntc � np),y el término independiente b es función de las observaciones, de dimensión (ntc),
A =
26666664N(xOBS1 )
@ T�tlIterRefract
�@ tl
(1)Refract
� � � N(xOBS1 )
@ T�tlIterRefract
�@ tl
(np)Refract
... . . . ...
N(xOBSntc)
@ T�tlIterRefract
�@ tl
(1)Refract
� � � N(xOBSntc)
@ T�tlIterRefract
�@ tl
(np)Refract
37777775 , (18)
b =
264tTOBS1 �N(xOBS1 ) T
�tlIterRefract
�...
tTOBSntc �N(xOBSntc) T
�tlIterRefract
�375 . (19)
Parametrización de la geometría
Como se ha mencionado en la sección anterior la geometría debe discretizarse utilizandoun conjunto de parámetros o variables escalares que la describan. Cada variable escalar oparámetro tl(i)Refract está asociado a un punto base y a un vector dirección, Fig.1, y a partirde éstos queda determinado un punto sobre la curva que de�ne la geometría buscada; enel problema en cuestión, esta curva corresponde a la isoterma de 1150�C.
31

Siete parámetros son utilizados para de�nir la geometría del problema, estando lospuntos base y vectores dirección elegidos de forma tal de utilizar la información queproporcionan las termocuplas instaladas en el crisol del alto horno.
Base Pointand
Direction Vector
Figura 1: Conjunto de parámetros que de�nen la geometría.
Introducción de restricciones en la solución
Resulta necesario resolver el problema inverso de estimación introduciendo restriccionesen la solución, y en particular restricciones que involucran el cumplimiento de desigualdades.Concretamente es necesario introducir restricciones en la variable tlRefract de forma talque no adopte con�guraciones fuera de límites dados por la propia geometría del crisol, yesto conlleva a la necesidad de introducir restricciones del tipo
g( tlRefract) � 0 . (20)
La iteración k del Método Iterativo de Regularización de Gauss-Newton puede serreescrita como la minimización del siguiente funcional
Fk =1
2
tT �xOBSi ; tlkRefract�� tTOBSi + D tT
�tlkRefract
� �tlRefract � tlkRefract
� 2+1
2� L� tlRefract � tl4Refract
� 2 i = 1; ntc . (21)
32

y por lo tanto la introducción de restricciones en la solución se realiza minimizando elfuncional Fk sujeto a las condiciones de desigualdad
minimizartlRefract
Fk (22)
sujeto a g( tlRefract) � 0 . (23)
Utilizando el método de penalización [10] se tiene
minimizartlRefract
Fk+1 + { P�tlRefract
�, (24)
donde P (tlRefract), cuando se discretiza el problema con un número discreto de parámetrosnp, tiene la forma
P (tlRefract) =1
2
npXi=1
�max
�0; gi
�tlRefract
���2 (25)
siendo, por ejemplo,gi =
tl(i)Refract � maxl
(i)Refract . (26)
Por lo tanto cada paso iterativo queda de�nido como
tlIter+1Refract =tlIterRefract+
�Iter�ATA+� LTL+C
��1 � �ATb+� LTL�tl�Refract � tlIterRefract
�� c�, (27)
donde la matriz C y el vector c tienen la forma
Cii =
npXi=1
{max
�0; gi
�tlIterRefract
��gi�tlIterRefract
� "@ gi
�tlIterRefract
�@ tl
(i)Refract
#2; Cij = 0 8 i 6= j (28)
ci =
npXi=1
{@ gi
�tlIterRefract
�@ tl
(i)Refract
max�0; gi
�tlIterRefract
��. (29)
La Fig. muestra un diagrama de �ujo del esquema iterativo de cálculo utilizado.
Determinación de los operadores de sensibilidad
Los operadores de sensibilidadDtlRefractF han sido discretizados utilizando el mismosoporte de elementos �nitos utilizado para el cálculo de la función t ~T , siendo
@ ~T ( tlRefract)
@tl(i)Refract
= N(x)@T ( tlRefract)
@tl(i)Refract
. (30)
33

tTiOBS i = 1,n tc
Iter = 0
Directproblem
Sensibilityequations
T tl RefractIter
/T tl RefractIter
/ t lRefractÝiÞ
bi =t TiOBS ? NÝxi
OBS Þ T tl RefractIter
Iter = Iter + 1
Functionevaluation
andminimization
ConvergenceYes
No
Ai,j= NÝx iOBSÞ
/ T tl RefractIter
/ tlRefractÝjÞ
K Iter
Determination ofK Iter
Determination of
tl RefractIter+1 = tl Refract
Iter + K Iter A tlRefractIter
J = N2
2X+1
Cii = CiiÝg iÞ ci = ciÝg iÞ
A tl RefractIter = ßATA+J LTL + Cà?1 6 ATb +J LTL tl Refract
A ? tl RefractIter ? c
t T Iter+1? t T Iter
K Iter t T Iter² TOL
34

Como la función t ~T no posee en forma explícita las variables tlRefract ya que sonparámetros que caracterizan a la geometría del problema, es decir, al dominio en el cual se
resuelven las ecuaciones diferenciales, las derivadas@ ~T ( tlRefract)
@tl(i)Refract
no podrán calcularse
analíticamente. Por lo tanto, se calcularán de la siguiente manera
@ ~T ( tlRefract)
@tl(i)Refract
' N(x)
24T�tlRefract + �
(i)"��T ( tlRefract)
"
35 . (31)
donde �(i) es un vector con todas sus componentes iguales a cero excepto la componentei que vale 1.
FORMULACIÓNDELPROBLEMADIRECTODETRANSFERENCIADE CALOR
Los problemas de conducción de calor estacionarios están caracterizados por lasiguiente ecuación diferencial
r � (krT ) = 0 8x 2 , (32)
donde k es el tensor de conductividad térmica, y es un dominio abierto y acotado, con � Rndim (1 � ndim � 3), cuya frontera suave es @.
La Ec.32 está sujeta a las siguientes condiciones de borde sobre @T , @q y @c(cumpliéndose @T[@q[@c = @, @T\@q = 0, @T\@c = 0 y @q\@c = 0):
� Condición de borde tipo Dirichlet: temperatura Tw impuesta sobre @T ,
T = Tw 8x 2 @T . (33)
� Condición de borde tipo Neumann: �ujo qw impuesto sobre @q,
�krT � n = qw 8x 2 @q, (34)
donde n es el vector normal exterior a @.� Condición de borde tipo Robin o mixta: generalmente está asociada a un �ujo decalor por convección o a una ley de enfriamiento de Newton, contra un medio atemperatura T1,
qconv = h (T � T1) 8x 2 @c. (35)
35

La solución del problema por medio del método de los elementos �nitos implicala adopción de funciones de dimensión �nita, Ec.15; por lo tanto introduciendo estasfunciones de dimensión �nita en la ecuación diferencial, Ec.32, y utilizando el método deGalerkin [11], se obtiene el sistema de ecuaciones:
KT� F = 0, (36)
donde K es la matriz de conductividad o de rigidez y F es el vector de cargas, de�nidospor:
K =
Z
BTkB dV| {z }Kcond
+
Z@c
hNTN dS| {z }Kconv
, (37)
F = �Z@q
NT qw dS| {z }Fq
+
Z@c
hNTT1 dS| {z }Fconv
, (38)
siendo B la matriz gradiente, Bij =@Nj@xi
; y debiéndose imponer en el sistema deecuaciones las condiciones de borde tipo Dirichlet.
Lowerhearthspray
Lowerhearthspray
Lowerhearthspray
Lowerhearthspray
Air (Bottom cooling)
hwater
Twater
hair Tair
1150°C Isotherm
Figura 2: Condiciones de borde utilizadas en el problema directo.
Sobre la geometría de�nida por el conjunto de parámetros tlRefract se construye unamalla de elementos �nitos, utilizando elementos de cuatro nodos, y se aplican condicionesde borde consistentes con el problema (Fig.2):
36

� Temperaturas impuestas sobre la curva correspondiente a la isoterma de 1150�C(condiciones de borde tipo Dirichlet).
� Convección forzada entre la chapa de acero y el aire que refrigera el plenum, dadapor un coe�ciente hair y por una temperatura Tair (condición de borde tipo Robin omixta).
� Convección forzada entre la chapa de acero y el agua que refrigera la super�cielateral del crisol, dada por un coe�ciente hwater y por una temperatura Twater (condiciónde borde tipo Robin o mixta).
Es importante destacar que durante la evolución histórica del estado térmico del crisolel conjunto de parámetros tlRefract irá cambiando y, consecuentemente, un algoritmo deremallado es necesario para reconstruir la malla de elementos �nitos en cada con�guración.
El algoritmo de remallado desarrollado, sigue los siguientes pasos para construir lamalla de elementos:
1. Contruir una malla estructurada con elementos de cuatro nodos, asociados a diferentesmateriales, respetando la geometría y características del crisol.
2. Utilizar los puntos determinados por el conjunto de parámetros tlRefract para construiruna función �(x), de�nida en el mismo espacio R2 en el que está de�nida la mallade elementos �nitos, que toma valores menores a cero en la zona de �material� yvalores mayores a cero en la zona de �no material�. La función de interpolación�(x) se construye utilizando Funciones de Base Radial (Radial Basis Functions)cuyas características principales se indican en el Apéndice B.
3. Eliminar nodos y elementos de la malla estructurada que no forman parte de la zonade �material�, respetando los materiales y características geométricas del crisol,siguiendo el algoritmo descripto en el Apéndice C.
4. Luego, resolver un problema de optimización para posicionar los nodos sobre lafrontera �material / no material�, el cual está descripto en el Apéndice C.
5. Por último, aplicar las condiciones de borde de temperatura impuesta sobre laisoterma de 1150�C (frontera �material / no material�) y las condiciones de bordede convección correspondientes.
37