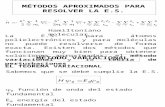Las Páginas de Ruben Labato - III. `TOMOS POLIELECTRÓNICOS · 2013-06-17 · es la estimación de...

III. ÁTOMOS POLIELECTRÓNICOS 1

3 -1. Introducción

Para átomos que contienen más de un electrónla forma de la ecuación de Schrödinger es máscomplicada, porque la expresión de la energía in-cluye términos para las interacciones de repulsiónentre los diferentes electrones. Incluso para elhelio, con dos electrones, la ecuación deSchrödinger es demasiado compleja para resol-verse de manera explícita aunque se pueden obte-ner con cierta facilidad soluciones numéricas. Pa-ra átomos más complejos se utilizan solucionesaproximadas y aún así suele ser imposible obtenersoluciones explícitas. Sin embargo, con las com-putadoras modernas estos métodos aproximadospermiten lograr soluciones numéricas en un tiem-po razonable.

En general, se escribe la ecuación deSchrödinger

EH

1 Extractado de: Levine, I. N. Quantum Chemistry 5th.Edition Prentice – Hall. Upper Saddle River. 2000 yMcQuarrie, D.A. – Simon, J. D. Physical Chemistry. AMolecular Approach. University Science Books. Mill Val-ley. 2000. Szabo, A – Ostlund, N.S. Modern QuantumChemistry. Dover Pub. Inc. Mineola. 1996; Bohm D. Quan-tum Theory. Dover Pub. Inc.New York. 1993. Pauling, L –Bright Wilson Jr, E. Introduction to Quantum Mechanics,Dover Pub. Inc.New York. 1985.

y se trata de establecer el conjunto de valores parala energía

Eii (i= 1, 2, 3, ...)

No habiendo métodos teóricos, o solucionesde la ecuación de Schrödinger se recurre a méto-dos aproximados.

3 - 2. Métodos aproximados

Algunos de los métodos aproximados utilizanla aproximación al campo central. Recordemosque un campo se dice central cuando la energíapotencial de cualquier punto material ubicado enél depende únicamente de su distancia a un punto.

Mediante esta aproximación se analiza el mo-vimiento de un electrón, generalmente el más ex-terno del átomo, suponiendo que todos los demáselectrones forman una “nube de carga eléctrica”que tiene, en promedio, simetría esférica. Elelectrón considerado se mueve en un campo eléc-trico generado por el núcleo y los demás electro-nes. De este modo, la carga generadora del campoeléctrico ya no es Ze sino una carga nuclear efec-tiva Zefect e inferior a la carga nuclear verdadera.Con esta aproximación, puede suponerse al átomocomo teniendo un solo electrón. Sobre esta base,se plantea la ecuación de Schrödinger que difierede la aplicable al átomo de hidrógeno en el valorde la energía potencial. La suposición de que elcampo eléctrico tiene simetría esférica permiteque las ecuaciones diferenciales () y () se-an las mismas que para el átomo de hidrógeno.Los números cuánticos y m tienen el mismosignificado que en el caso del átomo de hidróge-no, al igual que la componente del momento an-gular orbital según el eje z, pero al variar la fun-ción de la energía potencial variarán los valorespropios de E que surgen de la resolución de laecuación radial.

DEPARTAMENTO DE FÍSICA - CÁTEDRA DE MECÁNICA CUÁNTICA

Profesor: Dr. Miguel Katz

86

Una aplicación sencilla de este procedimiento,es la estimación de la energía de ionización, quees la energía necesaria para llevar al electrón desu orbital externo del átomo aislado a una distan-cia infinita.

En el modelo de Bohr, aplicado a átomoshidrogenoides, la energía potencial del electrón enun estado estacionario para un valor n, está dadapor

200

22 14 na

eZUn (3 - 1)

La misma expresión para Un se obtiene median-te el tratamiento mecánico - cuántico.

El valor absoluto de esa energía para Z = 1 yn = 1 es 4,36 × 10 -18 J o 27,2 eV y es frecuentellamar a esta cantidad unidad atómica de energía(ua), también se la conoce como hartree en honoral físico británico Douglas Rayner Hartree (1897- 1958). El radio de Bohr, a0 = 5,292 × 10-11 m seconoce como unidad atómica de longitud.

La energía total del electrón, tanto en el mo-delo de Bohr como en mecánica cuántica es

200

22 18 na

eZEn

Esta es sólo la mitad de la energía potencial ycambiada de signo da el valor de la energía de io-nización I para el electrón de número cuántico n.Por lo tanto la energía de ionización estará dadapor

J,n

ZnZ

aeI 18

2

2

2

2

00

2

1036428

uan

Z2

2

2

(3 - 2)

Para aplicar la aproximación al campo central,simplemente se sustituye Z por Zefect.

uan

ZI efect

2

2

2 (3 - 3)

Esta aproximación es utilizada en los llamados“métodos Hartree – Fock” para la resolución deecuaciones de onda mediante funciones de ondamonoelectrónicas en un campo central.

3 - 3. El método de variación o método va-riacional

En mecánica cuántica hay un procedimiento muypoderoso que constituye la base de la mayoría de loscálculos efectuados sobre átomos y moléculas. Cono-cido como método de variación, no sólo permite efec-tuar cálculos confiables para átomos complejos (ymoléculas) sino que también permite estudiar los enla-ces químicos.

Este método consiste en buscar una función deprueba que tiene que depender de las mismas varia-bles que la función de onda. Esta función de pruebatiene que obedecer las mismas condiciones de contor-no que la función exacta.

Por ejemplo, para la partícula en una caja (Figura3 - 1), las condiciones son que la función valga 0 en elexterior de la caja y en x = 0 y x = L. La función deonda toma la forma

xL

nsenL

/

)x(n

212 (n = 1, 2, 3, ...) (1 - 66)

Si se intenta utilizar como función de pruebala expresión

36 xxxAnx

se encuentra que, si bien nx es cero para x = 0, esdistinta de cero para x = L. Al no cumplir con lascondiciones impuestas al sistema cuya función deonda se conoce no puede utilizarse como funciónde prueba. En cambio la función

CAPÍTULO III - ÁTOMOS POLIELECTRÓNICOS 87

xLxnx

cumple con valer cero tanto para x = 0 como parax = L. Utilizando esta función de prueba se for-mula la ecuación

EH

se multiplica ambos miembros por la complejaconjugada

*EE*H* aproxaprox

Figura 3 - 1. Representación de 2 = f(x) conn = 1 para una partícula en una caja

Integrando ambos miembros sobre el espaciocompleto

d*EdH* aprox

y, por lo tanto

d*

dH*Eaprox

(3 - 4)

En el caso en que la función esté normalizada,el denominador de esta ecuación vale 1

Para calcular el valor medio de la energía proce-demos de la siguiente manera:

Sabemos que el hamiltoniano para una partí-cula dentro de una caja unidimensional es

2

22

2 dxd

m

Por lo tanto, para el numerador de la (3 - 4) escri-bimos

L

L

dxLxxm

dxxxLdxdxxL

mdH*

0

22

2

02

22

2

2

mL

6

32

y para el denominador escribimos

30

52

0

2 LdxxLxd*L

con lo que

22

2

2

2

455

mLh

mLd*

dH*

y, si se compara con el que corresponde a la fun-ción exacta

2

22

8mLhnEn (n = 1, 2, 3, ...) (1 – 63)

Se encuentra que



88

01321102

0

,E

Eaprox

Esto es, para el estado fundamental Eaprox es 1,3% mayor que el valor de E0 calculado con la (1 -66).

La utilidad del método de variación se asientaen el llamado principio de variación (tambiénllamado teorema variacional)

Supongamos que E0 es la más baja energíapermitida del sistema, la energía del estado fun-damental. Entonces si es la función de ondaaproximada

0EdH* (3 - 5)

Este teorema nos dice que

La energía calculada a partir de cual-quier función de prueba no puede ser infe-rior al valor verdadero de la energía basaldel sistema

Para demostrar el teorema variacional bastadefinir una integral

dEHI *0 (3 – 6)

y demostrar que esta integral es 0.

00 EdHdEdHI ***

si la función está normalizada.

Si demostramos que I 0 habremos demos-trado la (3 – 5)

Hagamos iy Ei las funciones propias y losvalores propios verdaderos de H tal que,

iiEH (3 - 7)

Como las funciones propias i forman un con-junto completo es posible desarrollar en térmi-nos de i (Nótese que esto implica que satisfa-ga las mismas condiciones límites que i)

kkka (3 – 8)

Sustituyendo en la (3 – 6) se obtiene

daEHa

daEHaI

kj

jj

*k

*k

jj

jk

*k

*k

0

0

(3 – 9)

Aplicando la (3 – 7) y suponiendo que es váli-do el intercambio entre la integración y las suma-torias infinitas, obtenemos

dEEaa

dEEaaI

j*kjj

k j

*k

jjj

jk

*k

*k

0

0

(3 – 10)

Haciendo uso de la ortogonalidad de las fun-ciones propias

k j

kjjj*k EEaaI 0 (3 – 11)

Llevando a cabo la suma sobre j y recordandoque el factor kj de Kronecker anula todos lostérminos excepto aquel en el que j = k, se en-cuentra

k

kkk

kk*k EEaEEaaI 0

20

(3 – 12)

Como por hipótesis E0 es el valor propio másbajo tendremos que Ek – E0 tiene que ser mayor o


igual que cero. Como el valor absoluto de ak, ele-vado al cuadrado es mayor o igual que cero, resul-ta que

I 0

lo que implica que

000 dEdHdEHI ***

(3 – 13)

o

dEdH **0 (3 – 14)

y

0Ed

dH

*

*

(3 – 15)

Si se normaliza la función el denominadorde la (3 – 15) es 1 y se obtiene el resultado desea-do

0EdH* Este resultado tiene una importancia enorme

ya que nos asegura que cualquiera sea la funciónde prueba aproximada que utilicemos el valorpropio que obtenemos no se encuentra nunca pordebajo del valor real, evitando pasar de diferen-cias positivas a diferencias negativas por el cam-bio de la función de prueba o adición de otras.

De este modo se puede lograr una mayoraproximación al valor exacto de la energía si sevan agregando a la función de prueba otras fun-ciones de prueba que actúan como términos adi-cionales. Con el agregado de nuevos términos se

obtiene sucesivamente mejores aproximaciones alvalor exacto.

3 – 3.1. Funciones variacionales lineales

Un tipo especial de función variacional am-pliamente utilizado, especialmente en el estudiode las funciones de onda de moléculas, es la fun-ción variacional lineal, que es una combinaciónlineal de un conjunto de n funciones de pruebalinealmente independientes 1, 2, ... ,n, quecumplen con las condiciones de contorno impues-tas

n

iiinn aaaa

12211 (3 – 16)

donde es la función variacional de prueba y loscoeficientes ai son parámetros a determinar mini-mizando la integran variacional. Las funciones deben, obviamente, satisfacer las condicioneslímites del problema.

Para simplificar el tratamiento nos limitare-mos a considerar que es real de modo que todoslos coeficientes ai y las funciones son reales.

Al aplicar el teorema de las variaciones co-mentado en el párrafo anterior tenemos para lafunción variacional lineal real

daa

daad

k

n

jj

n

kkj

n

j

n

kkkjj

*

1 1

1 1

(3 – 17)

Definimos la integral de solapamiento Sik co-mo



90

dS k*jjk (3 – 18)

Con lo que la (3 -16) se puede escribir

jk

n

j

n

kkj

* Saad

1 1

(3 -19)

La integral de solapamiento no es necesaria-mente igual a ik ya que no hay ninguna razón pa-ra suponer que las funciones i yk sean mutua-mente ortogonales, con lo que no son necesaria-mente funciones propias de ningún operador.

Para el numerador de la (3 – 15) tenemos

dHaa

daHadH

k

n

jj

n

kkj

n

kkk

n

jji

*

1 1

11

(3 – 20)

Haciendo

jkk*j HdH

se puede escribir

jk

n

j

n

kkj

* HaadH

1 1

(3 – 21)

La integral variacional W es

jk

n

j

n

kkj

jk

n

j

n

kkj

*

*

Saa

Haa

d

dHW

1 1

1 1 (3 – 22)

a partir de la cual, podemos escribir

jk

n

j

n

kkjjk

n

j

n

kkj HaaSaaW

1 11 1

(3 – 23)

Se debe minimizar W, de manera de aproximarnostanto como sea posible a E0, (W E0). La integralvariacional W es una función de las n variablesindependientes (a1, a2, ... ,an) . Esto es

W = W(a1, a2, ... ,an) (3 – 24)

Una condición necesaria para obtener unmínimo en W es que su derivada parcial con res-pecto a cada una de las variables sea nula

n,,,iaW

i

210

(3 – 25)

Derivando la (3 – 23) respecto a cada ai se ob-tienen n ecuaciones:

n,,,iHaaa

Saaa

WSaaaW

jk

n

i

n

kkj

i

jk

n

j

n

kkj

ijk

n

j

n

kkj

i

211 1

1 11 1

(3 – 26)Ahora

jk

n

j

n

kkj

ijk

n

j

n

kkj

i

Saaa

Saaa

1 11 1

jk

n

j

n

k i

kj

i

jk S

aaa

aa

a

1 1

(3 – 27)

Las aj son variables independientes y, por lotanto,

ijsiaa

i

j

0 y ijsi

aa

i

j

1 (3 – 28)


Condiciones que pueden escribirse

iji

j

aa

(3 – 29)

Entonces tenemos

jkik

n

j

n

kjjkij

n

j

n

kk

jk

n

i

n

kkj

i

SaSa

Saaa

1 11 1

1 1

jk

n

jjjk

n

kk SaSa

11

(3 – 30)

como estamos tratando con funciones reales

ij*ijji SSS (3 – 31)

ik

n

kkik

n

kk

ij

n

jjik

n

kkjk

n

j

n

kkj

i

SaSa

SaSaSaaa

11

111 1

ik

n

kkjk

n

j

n

kkj

i

SaSaaa

11 1

2 (3 – 32)

Siendo H un operador hermítico y tanto lasfunciones como el hamiltoniano reales, se verificaque

ij*ijji HHH (3 – 33)

Por lo tanto, se puede sustituir Sjk por Hjk conlo que obtenemos

ik

n

kkjk

n

j

n

kkj

i

HaHaaa

11 1

2 (3 – 34)

Sustituyendo las ecuaciones (3 – 25), (3 – 32)y (3 – 34) en la (3 – 26)

n,,,iHaSaW ik

n

kkik

n

kk 2122

11

(3 – 35)

n,,,iaWSH kikik

n

k

2101

(3 – 36)

Se establecen así n ecuaciones linealeshomogéneas simultáneas para las n incógnitas a1,a2, ..., an.

Para encontrar la solución de un sistema deecuaciones lineales homogéneas existen dos posi-bilidades: o considerar que todos los ai son nulos(en cuyo caso la función variacional es nula) oque debe ser nulo el determinante de los coefi-cientes. En este último caso se plantea el determi-nante

0

2211

2222222121

1112121111

WSHWSHWSH

WSHWSHWSHWSHWSHWSH

nnnnnnnn

nn

nn

(3 – 37)

donde Hij =i H j

d*S jiij (integral de solapamiento)

H*W (valor medio de la energía)

Recordemos que



92

Hij =i H j = dH* ji para Sji = 1

Al desarrollar el determinante se encuentra unpolinomio de grado n en la incógnita W con n raí-ces (reales)

Pol (W)n = 0

Agrupando las raíces en orden creciente

W1 W2 W3 … Wn

Agrupando los estados del sistema en orden deenergía creciente, tenemos

E0 E1 E2 E3 ... En -1 En En +1 ...

Se puede probar 2 que

W1 E0W2 E1W3 E2

... Wn En-1

A diferencia del ejemplo de la partícula en unacaja en el que se encuentra la aproximación al es-tado fundamental, en este caso, mediante las fun-ciones de prueba nse encuentranenergías aproximadas para los estados excitados.

El método de variación lineal proporciona unlímite superior de la energía para los n primerosestados del sistema utilizando las raíces W1, W2,..., Wn, como aproximaciones. Si se quiere unamayor aproximación se toma mayor cantidad defunciones aproximadas. En este caso W’1 seaproxima más a E0, W’2 se acerca más a E1 y asísucesivamente.

2 J.K.L. MacDonald, Phys. Rev. 43, 830 (1933)

Problemas:

1. Sea = exp(-x2) una función de prueba nonormalizada para un oscilador armónico unidi-mensional siendo las dimensiones de : m-2. (a)verifique que la función es de buen comporta-miento y que cumple con las condiciones impues-tas al oscilador armónico (b) Utilizando el métodovariacional establezca la energía mínima que co-rresponde para esta función.

Solución:

a) La función es de cuadrado integrable. Tienevalores finitos aún para . Siendo x una longi-tud cumple con el requisito de hacer adimen-sionado el exponente de e.

b) La energía (aproximada) que corresponde a es-ta función de prueba viene dada por

d

dHE

*

*

Aprox

El operador hamiltoniano es

2222

22

22

mxdxd

m

donde es la frecuencia de vibración del oscila-dor

0

2222

2222

22

dxemxdxd

me

dH

xx

*

dxexmdxedxde

mxxx 222 222

2

22

22

cuya resolución da


23215

221212

88/

//

/* m

mdH

0

22 222 dxedxed xx*

= 2121

2/

/

Por lo tanto, la integral variacional es

1

222

22

mmd

dH

*

*

Debemos encontrar el valor de que hagamínimo el valor de la energía. Llamando W al co-ciente de las integrales, la condición para obtenerel mínimo es que dW/d = 0. Esto es

0122 2

20

22

mm

o sea 2

220

22

m

Donde hemos reemplazado por 0 – la fre-cuencia del estado fundamental - con lo que

m0

La raíz negativa de debe rechazarse ya queharía que la función de prueba no fuera de cua-drado integrable. Por lo tanto

m0

2. ¿Qué valor de la energía basal se obtienepara el oscilador armónico usando el valor de encontrado en el ejercicio anterior?

Solución:

La energía vendrá dada por

d

dHE

*

*

0

122

20

22

mm

Reemplazando por

m0

0000

0 21

22

hE

En este caso coincide el valor de la energíacon el verdadero.

3. Una función de prueba normalizada se ex-presa en unidades atómicas como

rer!

27

642

Al resolver la integral variacional se obtiene

310

2

dHW *

Complete el procedimiento variacional a finde minimizar el valor de la energía

Solución:

Se trata de encontrar el valor que hace mínimoa dW/d.



94

31

5310

2

d

d

Igualando a cero

031

50

Se encuentra

35

0

Por lo tanto, la energía del estado fundamentalE0

a.u,//E 277703

3510

35 2

0

3 - 4. Método de perturbación

Otro método que se ha empleado para tratarlas energías de repulsión interelectrónicas es elmétodo de perturbación. Este método fue inicial-mente utilizado para encarar problemas de Mecá-nica Celeste. Es bien sabido que en la Mecánicanewtoniana sólo es posible resolver con exactitudproblemas de interacción entre dos cuerpos (porejemplo, problemas de interacción entre la Tierray el Sol o entre la Luna y la Tierra.). Pero no pue-den despreciarse las fuerzas interplanetarias yconsiderar solamente la atracción que ejerce elSol sobre los planetas ya que muchos fenómenosdelicados están asociados con esas interaccionesadicionales (en relación a esto, vale la pena recor-dar que Leverrier predijo la existencia de Neptunosobre la base de las desviaciones orbitales deJúpiter y que tiempo después ese planeta fue des-cubierto por los astrónomos). De manera que, en

el siglo XIX se tornó necesario considerar los pro-blemas de interacción entre varios cuerpos, quecarecen de solución exacta en la Mecánica Clási-ca. En Mecánica Celeste se encontró que losproblemas de las perturbaciones pueden ser trata-dos mediante una aproximación basada sobre elhecho de que las fuerzas entre los planetas sonmucho menores que la fuerza de atracción con elSol. En este método, se parte de resolver el pro-blema de dos cuerpos (lo que usualmente se llamaaproximación de orden cero) y luego se toma encuenta la perturbación producida por los demáscuerpos y se trata de encontrar las correcciones aesa solución (la llamada aproximación de primerorden). En otras palabras, el método de perturba-ción involucra considerar las fuerzas principalesque actúan sobre un cuerpo, encontrar la soluciónrigurosa para la interacción de esas fuerzas y, en-tonces, tomar en cuenta las fuerzas “perturbado-ras”.

De manera análoga, en el tratamiento mecáni-co – cuántico del movimiento de varios electronesen un átomo, es necesario considerar primero lasfuerzas principales que actúan como, por ejemplo,la fuerza entre el núcleo y un electrón. En este ca-so, las fuerzas perturbadoras a tener en cuenta sonlas fuerzas de Coulomb de repulsión mutua entrelos electrones. En el problema de un átomo sujetoa un campo externo, eléctrico o magnético cuyaintensidad es pequeña en comparación con elcampo eléctrico generado por el núcleo, se consi-dera que la perturbación es la energía del electrónen el campo externo.

El método de perturbación fue el primermétodo aproximado utilizado en la Mecánica On-dulatoria y fue desarrollad por Schrödinger en sutercer trabajo publicado en la primavera de 1926.Aunque al estudiante le parezca complicado, elmétodo mecánico-cuántico de perturbación esmenos complicado que el utilizado en la Mecáni-ca Celeste.


3 – 5. Método de perturbación para siste-mas en estados estacionarios.

Supongamos que el sistema en estudio tieneun hamiltoniano Ĥ independiente del tiempo cuyaforma impide resolver la ecuación de Schrödinger

ĤYn = EnYn (3 – 38)

de manera exacta mediante los métodos matemá-ticos disponibles y obtener las funciones propias yvalores propios de los estados estacionarios enla-zantes. Si el hamiltoniano Ĥ es ligeramente dife-rente de otro hamiltoniano Ĥ0 de un sistema delcual se conoce la solución exacta

0000nnn EH YY (3 – 39)

el método de perturbación da un resultado satis-factorio.

Un ejemplo, es el oscilador anarmónico unidi-mensional con el Hamiltoniano

4322

2

21

2dxcxkx

dxd

mH

(3 – 40)

que está muy relacionado con el Hamiltoniano deloscilador armónico, dado por

22

20

21

2kx

dxd

mH

(1 – 33)

Si las constantes c y d en la Ecuación (3 - 40)tienen valores pequeños, puede considerarse quelos términos cx3 y dx4 introducen pequeñas per-turbaciones en el oscilador armónico trans-formándolo en un oscilador anarmónico y es deesperar que las funciones propias y los valorespropios de este oscilador anarmónico sean muyparecidas a las del oscilador armónico.

Se acostumbra a llamar al sistema con hamil-toniano 0H sistema sin perturbar. El sistema conhamiltoniano Ĥ es el sistema perturbado. La dife-

rencia entre los dos hamiltonianos es la perturba-ción, Ĥ':

Ĥ’= Ĥ - 0H (3 – 41)

de donde el hamiltoniano del sistema en estudioes

Ĥ = 0H + Ĥ’ (3 – 42)

(La prima no indica aquí diferenciación). Para eloscilador anarmónico con el Hamiltoniano (3 -40) la perturbación con respecto al osciladorarmónico es Ĥ’ = cx3 + dx4.

En la ecuación (3 -39) 0nE y 0

nY son las deno-minadas energía sin perturbar y función de ondasin perturbar del estado n. So el hamiltoniano

0H corresponde al oscilador armónico, dado porla Ecuación (1 - 33), entonces 0

nE es igual a (n+1/2)hn donde n es un número entero no negati-vo. (Se usa n en lugar de v por coherencia con lanotación de la teoría de perturbaciones.) Nóteseque el superíndice no se refiere al estado funda-mental. La teoría de perturbaciones puede aplicar-se a cualquier estado. El subíndice n denota el es-tado que se quiere evaluar, y el superíndice (0) ca-racteriza al sistema sin perturbar.

El objetivo es relacionar las funciones propiasy valores propios desconocidos del sistema per-turbado con las funciones propias y valores pro-pios conocidos del sistema sin perturbar. Para lle-var a cabo esta tarea, se puede imaginar que laperturbación se aplica gradualmente, produciendoun cambio continuo desde el sistema sin perturbaral sistema perturbado. Matemáticamente, estoequivale a introducir un parámetro en el hamil-toniano, de modo que

Ĥ = Ĥ0 + Ĥ' (3 - 43)

Cuando es cero, se tiene el hamiltoniano del sis-tema sin perturbar. Conforme aumenta , la per-turbación crece, y en = 1 la perturbación se ha



96

"aplicado" totalmente. se introduce por conve-niencia para relacionar las funciones propias per-turbada y sin perturbar. Al final del tratamiento seelimina, haciendo = 1.

3 – 6. Método de perturbación para siste-mas en estados estacionarios no degenerados.

Los tratamientos perturbativos de niveles deenergía degenerados y no degenerados son dife-rentes. En esta sección examinaremos el efecto deuna perturbación sobre un nivel no degenerado. Sialgunos de los niveles de energía del sistema sinperturbar son degenerados y otros son no degene-rados, el tratamiento desarrollado en esta secciónserá aplicable solamente a los niveles no degene-rados.

Sea 0nY la función de onda de un nivel deter-

minado no degenerado sin perturbar con energía 0nE . Sea Yn la función de onda perturbada en la

que se convierte 0nY cuando se aplica la perturba-

ción. De acuerdo con las Ecuaciones (3 - 38) y (3- 43), la ecuación de Schrödinger para el estadoperturbado es

nnnn E'HHH YYY 0(3 – 44)

Puesto que el Hamiltoniano en esta ecuación de-pende del parámetro , tanto las funciones propias

nY como los valores propios En dependen tambiénde :

q,nn YY y En = En

donde q denota las coordenadas del sistema. Des-arrollando nY y En en serie de Taylor de poten-cias de :

2

2

02

2

00

nnnn

YYYY (3 – 45)

2

2

02

2

00

nnnn

EEEE (3– 46)

Por hipótesis, cuando tiende a cero, nY tiende a 0

nY y En tiende a 0nE :

00 nn YY

y 0

0 nn EE

(3 – 47)

Las Ecuaciones (3 - 45) y (3 - 46) se transformanen

kn

knnnn YYYYY 2210 (3 – 48)

kn

knnnn EEEEE 2210 (3 - 49)

knY y k

nE se llaman correcciones de orden k dela función de onda y de la energía, donde k =1,2,3,... Supondremos que las series (3 - 48) y (3 -49) convergen para = 1, y cabe esperar que, pa-ra una perturbación pequeña, sea suficiente contomar los primeros términos de estas series paraobtener una buena aproximación a la energía y ala función de onda exactas.

Tomaremos 0nY de manera que esté normaliza-

da: 100 nn EY En lugar de la condición de

normalización, a la función nY le impondremosque satisfaga

10 nn YY (3 – 50)

Si nY no cumple esta condición, entonces, multi-

plicándola por la constante 1/ nn YY 0 obtene-

mos una función de onda perturbada que sí lacumple. La condición 10 nn YY denominada

normalización intermedia, simplifica el desarro-


llo. Dado que la multiplicación de nY por unaconstante no cambia la energía en la ecuación deSchrödinger, nnn Eˆ YYH , la utilización de lanormalización intermedia no afecta a los resulta-dos para las correcciones de la energía. Si sedesea, al final del cálculo se puede multiplicar lafunción nY , sujeta a la normalización intermedia,por una constante para normalizarla en el sentidousual.

Sustituyendo la Ecuación (3 - 48) en nn YY 01

[Ecuación (3 - 50)], obtenemos

202101001 nnnnnn YYYYYY

(Como 0 = 1, omitiremos expresarlo en las ecua-ciones posteriores).

Puesto que esta ecuación es válida para todos losvalores de comprendidos entre 0 y 1, los coefi-cientes de potencias similares de a cada lado dela ecuación deben ser iguales. Igualando los co-eficientes de 0, obtenemos

nn YY 01 , que se

cumple al estar 0nY normalizada. Igualando los

coeficientes de 1, de 2, y así sucesivamente, ob-tenemos

010 nn YY ; 020 nn YY ; etc. (3 – 51)

Nótese que cuando se utiliza la normalización in-termedia, las correcciones de la función de ondason ortogonales a 0

nY .

Sustituyendo las Ecuaciones (3 - 48) y (3 - 49) enla ecuación de Schrödinger (3 - 44), obtenemos

22102210

22100

nnnnnn

nnn

EEE'HH

YYY

YYY

y, agrupando los términos con potencias similaresde , queda

2011022

100100

1202

10000

nnnnnn

nnnnnn

nn

nnn

EEEEEE

'HH

H'HH

YYY

YYY

YY

YYY

(3 – 52)

Asumiendo que las series convergen adecuada-mente, para que cada una de las series que están aambos lados de la Ecuación (3 - 52) sean igualespara todos los valores de , se debe cumplir quelos coeficientes de potencias similares de enambas series sean iguales.

Igualando los coeficientes de los términos ,obtenemos 0000

nnn EH YY \ que es la ecuaciónde Schrödinger para el sistema sin perturbar (3 -32), y que no aporta ninguna información nueva.

Igualando los coeficientes de los términos 1,resultan

1001100nnnnnn EEH'H YYYY

0011010nnnnnn 'HEEH YYYY (3 – 53)

Para determinar 1nE multiplicamos la Ecuación

(3 - 53) por *m0Y e integrando en todo el espacio

se obtiene, expresando en la notación bracket

00001

100100

nmnmn

nmnnm

'HE

EH

YYYY

YYYY

(3- 54)

Como el hamiltoniano 0H ,es un operador hermí-tico, el primer término del primer miembro de laEcuación (3 - 54) queda:



98

010

010

001

001100

mnm

mnm

mmn

mnnm

E

**E

*E

*HH

YY

YY

YY

YYYY

(3 – 55)

donde hemos usado la ecuación de Schrödingersin perturbar 0000

nnn EH YY , y el hecho de quela energía 0

mE es real. Sustituyendo la Ecuación(3 - 55) en la (3 - 54): y usando la condición deortonormalidad

mnnm 00 YY para las funcio-

nes no perturbadas,

0011000nmmnnnmnm 'HEEE YYYY

(3 – 56)

Si m = n, el primer miembro de esta ecuación seanula y

d'H*'HE nnnnn00001 YYYY (3 – 57)

De esta manera, la corrección de primer orden dela energía se obtiene promediando la perturba-ción H' sobre las correspondientes funciones deonda sin perturbar. Haciendo = 1 en la Ecua-ción (3 - 49)

d'H*EEEE nnnnnn00010 YY

Problema:

4. Tomando al oscilador armónico como sistemano perturbado, obtenga la energía del estado fun-damental de un oscilador anarmónico cuyohamiltoniano es

4322

2

21

2dxcxkx

dxd

mH

Solución:

De acuerdo con la ecuación (3 – 42), el hamil-toniano de la perturbación, Ĥ’ es

Ĥ’ = Ĥ - 0H = 43 dxcx

y la corrección de primer orden de la energía parael estado con número cuántico v viene dada, deacuerdo con la Ecuación (3 - 57),

04301vvv dxcxE YY

Expresión en la que 0vY es la función de onda

para el oscilador armónico en el estado v. Para elestado fundamental, v = 0. En el Problema Nº 11de la Sección 1 – 22, hemos visto que, para el es-tado fundamental del oscilador armónico, la fun-ción de onda puede escribirse

241

00

2 /x/

ex

Y (3 – 58)

Por lo tanto

dxdxcxe

dxcxE

/x/

43221

00

4300

10

2

YY

De la Tabla de integrales encontramos que laintegral de la función impar

0322

dxcxe /x

Por lo tanto,


dxxedE /x/

4221

10

2

=

= dxxed /x/

4

0

221

2

2

De la Tabla de integrales encontramos que

21

1210

2

212312

/

nnbxn

bn···dxex

con b > 0, n = 1, 2, 3, … Siendo n = 2 y b =

2

10 4

3

dE

como

m 2 (Sección 1 – 22)

222

21

0 163

mdE

Para encontrar la corrección de primer ordenpara la función de onda, se considera que en laEcuación (3 – 56) m n por lo que mn = 0 y

001000nmnmnm 'HEE YYYY m n

(3 – 59)

Desarrollando 1nY en términos de un conjun-

to ortonormal completo formado por las funcio-nes propias sin perturbar 0

mY del operador hermí-tico Ĥ0

m

mmn a 01 YY donde 10nmma YY

(3 – 60)

Reemplazando este valor de am en la (3 – 59)

0000nmmnm 'HaEE YY (m n)

Como para nuestro desarrollo el estado 0nE

no está degenerado y m n

00

00

mn

nm

m EE

'Ha

YYm n (3 – 61)

Todos los coeficientes am del desarrollo de 1nY

dado por la (3 – 60) se calculan mediante la (3 –61) salvo el coeficiente an correspondiente a 0

nY .La segunda de las ecuaciones (3 – 60) nos diceque

10nnna YY

La elección de la condición de normalización in-termedia para Yn hace que 010 nn YY . Por lo

tanto

010 nnna YY

de modo que, mediante las ecuaciones (3 - 60) y(3 – 61) se obtiene, para la corrección de primerorden de la función de onda

nm

mmn

nm

n EE

'H0

00

00

1 YYY

Y (3- 62)

El símbolo m n indica que la suma se extiendesobre todos los estados sin perturbar excepto elestado n.

Haciendo = 1 en la ecuación (3 – 48) yusando solamente la corrección de primer ordende la función de onda, se obtiene como aproxima-ción a la función de onda perturbada

nm

mmn

nm

nn EE

'H0

00

00

0 YYY

YY (3 – 63)



100

Para las correcciones de segundo orden de laenergía, véase Levine, I. Química Cuántica. Cap.9. Las correcciones de segundo orden de la fun-cion de onda están bien tratadas en Kemble, E.C.The Fundamental Principles of Quantum Mecha-nics. Dover Pub. New York. 1958.

3 - 7. Números cuánticos de spin

La espectrografía atómica ha suministrado laevidencia de que muchas líneas espectrales, enrealidad, están formadas por dos líneas separadas,aunque muy próximas entre sí. Esto se conocecomo estructura fina. Así, el color amarillo que leconfiere el sodio a la llama corresponde a una ra-diación electromagnética que inicialmente secreyó que tenía una sola longitud de onda, (cuyalínea en el espectro es llamada línea D) pero queel desarrollo de instrumental más preciso permitióestablecer que se trata de dos líneas muy próxi-mas cuyas longitudes de onda son 5896 Å y 5890Å

Absorción

Emisión

Emisión ampliado en la línea D

Figura 3 – 2.- Espectros de absorción y deemisión del sodio.

Además del fenómeno de la estructura fina,los espectros de los átomos presentan característi-cas adicionales cuando se interpone un campomagnético.

Si se coloca un átomo de hidrógeno en uncampo magnético de densidad del flujo B, laenergía magnética de ese átomo estará dada por

Bm

emVm 2

(3 – 64)

El número cuántico m puede tomar 2 + 1 va-lores, de modo que cuando el átomo se encuentraen un campo magnético su estado cuántico sedesdobla en 2 + 1 estados cuyas energías difierenen (eħ/2m)B. Como, de acuerdo con la regla deselección, las variaciones de m están limitadas aml = 0. ± 1, una línea espectral dada que se pro-duzca en la transición entre dos estados de dife-rente , se escinde en solamente tres componen-tes. Esto se conoce como Efecto Zeeman normal.Esas componentes tienen frecuencias

Bm

ehB

me

42 001

01

Bm

ehB

me

42 001

En muchos casos, en vez de aparecer en el es-pectro tres componentes, suelen aparecer, debidoal desdoblamiento, cuatro, seis o siete líneas. Estose conoce como efecto Zeeman anímalo.

En un intento para explicar la estructura finade las líneas espectrales y el efecto Zeeman anó-malo, en 1925, George Eugene Uhlembeck y Sa-muel Abraham Goudsmit propusieron que elelectrón posee un momento angular intrínseco quees independiente del momento angular orbital quetiene debido a su movimiento respecto del núcleo.Asociado a ese momento angular intrínseco, elelectrón posee un momento magnético que seevidencia cuando el átomo se encuentra en uncampo magnético. Uhlembeck y Goudsmit supu-sieron que el electrón se comporta como una esfe-ra cargada girando sobre su propio eje, lo que ge-


neraría un momento magnético s adicional al co-rrespondiente al giro del electrón alrededor delnúcleo. De allí el nombre de spin asignado a eseefecto. El desarrollo de la Mecánica Cuánticaproducido a partir de 1926, desvirtuó completa-mente esa visión mecánico-clásica del comporta-miento del electrón. Si el Principio de incerti-dumbre impide conocer con exactitud la posiciónde un electrón en movimiento, menos se podríaestablecer la posición del eje del electrón respectode un campo externo y el sentido de giro alrede-dor de ese eje. El momento angular intrínseco delelectrón (y de otras entidades) es real, pero noexiste un modelo de la Física Clásica que puedarepresentar su origen de manera aceptable.

En 1928, Paul Adrien Maurice Dirac (1902 –1984) desarrolló una forma relativista de mecáni-ca cuántica que condujo a la conclusión de quepara un electrón hay dos componentes posibles demomento angular de espín. El vector de momentoangular de espín S es exactamente análogo almomento angular orbital L y está cuantizado demanera similar. La magnitud del vector S es

21 h)s(sS (3 – 41)

donde el número cuántico s solo puede tener elvalor +½. La componente Sz del momento angularde espín a lo largo del eje Z está cuantizado demanera similar a Lz

2hmS sz (3 – 42)

pero el número cuántico de espín ms, sólo puedetener los valores +½.y –½.

De esta manera, el espín del electrón es uncuarto grado de libertad que tiene esa partícula.En el mundo microscópico, además de las coor-denadas x, y, z, hay que indicar también el espínya que las funciones de onda dependen de las co-ordenadas espaciales, del espín y del tiempo.

Todas las partículas atómicas y subatómicastienen un cierto número de espín que puede serentero (0, 1, 2, ...) o fraccionario. Aquellas partí-culas que tienen número cuántico de espín enterose llaman bosones (pues obedecen a la estadísticade Bose - Einstein) y las que tienen número deespín fraccionario se llaman fermiones (pues res-ponden a la estadística de Fermi - Dirac).

3 - 6.- El principio de exclusión de Pauli

Sólo se ha obtenido una solución exacta de laecuación de Schrödinger para el átomo de hidró-geno: un sólo electrón moviéndose en el campogenerado por una carga positiva. En el caso de losátomos polielectrónicos los distintos métodosaproximados tienen que tomar en cuenta los cua-tro números cuánticos del electrón n, , m y ms.Una regla importante gobierna los números cuán-ticos permitidos a los electrones de un átomo. Es-ta regla es el llamado principio de exclusiónenunciado por Wolfgang Pauli en forma restringi-da en 1924 y luego en forma más general, lo quele confiere el carácter de postulado de la mecáni-ca cuántica.

El enunciado más restringido del principio deexclusión establece que

“En un átomo no pueden existir dos electro-nes con el mismo estado cuántico”

En el tratamiento de la estructura electrónicapor la aproximación del campo central, cadaelectrón es asignado a un orbital especificado porsus cuatro números cuánticos. De acuerdo con elprincipio de exclusión, dos electrones en el mis-mo átomo no pueden tener los mismos cuatronúmeros cuánticos.

Consideremos dos electrones A y B en unátomo. Cada electrón puede ser indicado por ungrupo de tres coordenadas espaciales (x, y, z) yuna coordenada de espín la cual puede tener va-



102

lores +½ y –½. Supongamos que se intercambianlas coordenadas espaciales y de espín de amboselectrones. Si bien los electrones son indistingui-bles, cuando se produce un intercambio de estaíndole podría ocurrir alguna de estas dos cosas:

a) La función de onda del sistema siguesiendo la misma (

b) La función de onda del sistema cambia designo (–

En el primer caso, se dice que la función essimétrica para el intercambio. En el segundo ca-so, la función es antisimétrica para el inter-cambio

La función de onda total para un electrón pue-de escribirse como el producto de dos funciones:una dependiente del espín () y la otra de las co-ordenadas ().

(x, y, z)

El enunciado del Principio de exclusión dePauli (independiente de la aproximación al campocentral y válido para fermiones en general) es elsiguiente

Una función de onda para un sistema deelectrones ha de ser antisimétrica para el inter-cambio de las coordenadas espaciales y de es-pín de todo par de electrones.

Si sólo hay intercambio de coordenadas

Si sólo hay intercambio de espín

De modo que siempre se cumpla

–

Dicho de otra manera: dos electrones con elmismo espín3 tienen probabilidad nula de encon-trarse en el mismo punto del espacio tridimensio-nal

El enunciado restringido de Pauli (en términosde números cuánticos) es un caso especial del ca-so general. Imaginemos dos electrones (1) y (2)en estados especificados por n1, 1, m1 y ms1 y n2,2, m2 y ms2. Una función antisimétrica sería

12

21

22221111

22221111

ss

ss

mym,,nmym,,n

mym,,nmym,,n

Si se intercambian (1) y (2), es necesario que– . Supongamos, sin embargo, que loscuatro números cuánticos fueran los mismos paralos dos electrones. Entonces esto es, nopuede existir tal estado.

Pauli también demostró que, de acuerdo con lateoría relativista del campo cuántico, que las fun-ciones de onda que describen el comportamientode fermiones son antisimétricas; mientras que lasfunciones de onda de bosones son simétricas. So-bre esta base, el Principio de exclusión se puedegeneralizar:

Una función de onda para un sistema defermiones idénticos ha de ser antisimétrica parael intercambio de las coordenadas espaciales yde espín de todo par de ellos.

El requisito de simetría o antisimetría de lafunciones de onda también se aplica a los siste-mas que contienen dos o más partículas compues-tas idénticas. Así, por ejemplo, una molécula de

3 Por "el mismo" espín, se entiende el mismo valor de ms. Elprincipio de exclusión de Pauli “obliga” a los electrones conel mismo espín a permanecer separados uno del otro; porello se habla a menudo de una repulsión de Pauli entre loselectrones. Esta "repulsión" no es una fuerza física real, sinoun reflejo del hecho de que las funciones de onda electróni-cas deben ser antisimétricas con respecto al intercambio.


16O2 tiene 8 protones y 8 neutrones en cadanúcleo. Tanto el protón como el neutrón son fer-miones con espín 1/2. Por lo tanto, el intercambiode dos núcleos de 16O supone el intercambio de16 fermiones, y lleva consigo la multiplicación dela función de onda molecular por (– 1)16 = 1. Demanera que la función de onda del oxígeno mole-cular 16O2 debe ser simétrica con respecto al in-tercambio de las coordenadas nucleares.

Al analizar el intercambio completo de dospartículas compuestas idénticas, que contienen jbosones idénticos y k fermiones idénticos, la fun-ción de onda se multiplica por (+l)j×(–l)k = (–l)k.Una partícula compuesta es, pues, un fermión sicontiene un número impar de fermiones, o unbosón si no es así.

Ejemplo

El Li natural es una mezcla formada por92,5% de 7Li y 7,5% de 6Li. En el núcleo de 6Lihay 6 fermiones (3 protones y 3 neutrones) y fue-ra del núcleo hay 3 electrones. Por lo tanto, el 6Lies un fermión. En cambio, el 7Li tiene 3 protones4 neutrones y 3 electrones, y es un bosón.

Cuando se usa el principio variacional paraobtener funciones de onda electrónicas aproxima-das de átomos y moléculas, el requisito de que lafunción variacional de prueba se comporte bienincluye que sea antisimétrica.

El principio de exclusión de Pauli es de granimportancia en el estudio de las configuracioneselectrónicas y nucleares de átomos polielectróni-cos e incluso moléculas.

El Principio de exclusión de Pauli sólo esaplicable a fermiones. Los bosones requieren unafunción de onda simétrica con respecto alintercambio y no hay restricción alguna en elnúmero de bosones que pueden ocupar un estadodado.

En 1925, Einstein demostró que para un gasideal cuyas partículas sean bosones no interac-tuantes, existe una temperatura muy baja Tc (lla-mada temperatura de condensación) por encimade la cual la fracción f de bosones que hay en elestado fundamental es despreciable. Por debajo deella, sin embargo, f se hace significativa, y tiendea 1 a medida que la temperatura absoluta T tiendea 0. La ecuación que permite calcular f para unsistema de bosones no interactuantes en una cajacúbica es f = 1 - (T/Tc)3/2 para T < Tc. 4 El fenó-meno en el que una fracción significativa de bo-sones cae al estado fundamental, se denominacondensación de Bose-Einstein. La condensaciónde Bose-Einstein fue importante para determinarlas propiedades del 4He líquido — cuyos átomosson bosones — que a temperaturas por debajo delos 3 K es superfluido y en el cual, las interaccio-nes interatómicas en el líquido dificultaban el aná-lisis teórico de sus variables de estado. .

En 1995, los físicos Eric Cornell y Carl Wie-man consiguieron producir la condensación deBose-Einstein en un gas 5. Usaron un gas de áto-mos de 87Rb. Un átomo de 87Rb tiene 87 nucleo-nes y 37 electrones. Con un número par (124) defermiones, el átomo de 87Rb es un bosón. Usandouna combinación de luz láser y la aplicación de uncampo magnético no homogéneo y radiación deradiofrecuencias, se consiguió enfriar una muestrade 104 átomos de 87Rb a una temperatura de 10-7

K, condensándose así una fracción sustancial deátomos en el estado fundamental. La radiación deradiofrecuencia se utilizó para eliminar la mayoríade los átomos que estaban en los estados excita-dos, dejando un condensado de 2000 átomos,prácticamente todos ellos en el estado fundamen-tal. Cada átomo de Rb en este experimento teníauna energía potencial dada por una función U(x,

4 Ver los detalles en McQuarrie (1973), Sección 10-4]5 [Physics Today, Agosto 1995, pág. 17; C.E. Wieman,

Am. J. Phys., 64, 847 (1996)] . También en 1995, WolfgangKetterle, del MIT, logró un condensado de átomos de sodio.Los tres compartieron el Premio Nobel de Física 2001.



104

y, z) producida por la interacción del momentomagnético de espín total del átomo y el campomagnético aplicado. El campo magnético in-homogéneo aplicado tenía una intensidad tal quela energía potencial generada sobre los átomos eraequivalente a la de un oscilador armónico tridi-mensional más una constante, de modo que losátomos de Rb en el condensado se comportabancomo si se encontrasen en el estado basal de esteoscilador armónico.

Problema:

5. Cuántos electrones pueden ocupar las si-guientes subcapas: (a) 1s); (b) 3p; (c) 3d y (d) 6g.

Solución:

Para un dado valor del número cuántico azi-mutal hay 2+ 1 valores posibles del númerocuántico magnético my, por lo tanto, hay 2 + 1orbitales. Como para cada orbital pueden existirhasta 2 electrones (a condición de que sus espinessean opuestos), la ocupación máxima será 2(2+1). Por lo tanto

2(2 + 1)(a) 1s 0 2(b) 3p 1 6(c) 3d 2 10(d) 6g 4 18

3 – 7. Determinantes de Slater

En 1929, John Clark Slater señaló que la fun-ción de onda antisimétrica para un sistema de Nelectrones podía escribirse con más comodidadcomo un determinante

N

NN

!NN,,,

nnn

bbb

aaa

21

2121

121

(3 – 43)

Los subíndices de las funciones pueden in-dicar los cuatro números cuánticos que especifi-can un orbital. Si permutamos dos filas cuales-quiera, cambia el signo del determinante. Lo queestá de acuerdo con el requisito de la asimetría. Siun grupo de cuatro números cuánticos llegara aser el mismo, por ejemplo a = b, entonces dos fi-las serían iguales y el determinante se anularía.

Por ejemplo, para el átomo de helio la fun-ción de onda de orden cero para el estado funda-mental es 1s(1)1s(2). Para tener en cuenta elespín, debemos multiplicar esta función espacialpor una función propia de espín. Analicemos lasfunciones propias de espín que son posibles paralos dos electrones. Para indicar que un electróntiene una cierta orientación (arbitraria) hacia“arriba” se suele utilizar el prefijo griego mien-tras que para indicar que un electrón tiene laorientación opuesta (hacia “abajo”) se emplea elprefijo griego Así una expresión del tipo (1)indica que el electrón 1 tiene espín hacia “arriba”o una expresión (2) indica que el electrón 2 tieneespín hacia “abajo”. Dado que cada electrón tienedos posibles estados de espín, para el átomo dehelio en el estado considerado tenemos, en princi-pio, las cuatro funciones de espín posibles si-guientes:

(1)(2) (1)(2) (1)(2) (2)(1)

Las funciones tercera y cuarta presentan unproblema: implican distinguir cual de los electro-nes tiene espín hacia “arriba” y cual hacia “abajo”lo que es imposible ya que ambos electrones sonidénticos, lo que los hace indistinguibles. Es porello que en lugar de emplear dichas funciones seemplean funciones de espín que son combinacio-nes lineales normalizadas de ambas del tipo


2-1/2 [(1) (2) (2)(1)]

De esta manera se tienen la cuatro funcionespropias de espín normalizadas para los dos elec-trones del helio en su estado fundamental

(1)(2),

(1)(2),

2-1/2 [(1) (2) + (2)(1)]

2-1/2 [(1) (2) - (2)(1)]

Las tres primeras son simétricas mientras quela cuarta es antisimétrica.

Corresponde ahora incluir el espín en las fun-ciones de onda del estado fundamental del helio.La función espacial 1s(1) 1s(2) es simétrica res-pecto del intercambio. Pero como el principio dePauli establece que la función de onda total, queincluya el espín, debe ser antisimétrica respectodel intercambio de los dos electrones, debe multi-plicarse la función espacial simétrica 1s(1) 1s(2)por una función de espín antisimétrica. Como solohay una función de espín antisimétrica, la funciónde onda del estado fundamental de orden cero pa-ra el átomo de helio que incluye el espín es

1s(1) 1s(2) 2-1/2 [(1) (2) - (2)(1)]

(3 – 44)

Como la configuración del estado fundamental(1s)2 del helio incluye los orbitales-espín 1s y1sel determinante de Slater puede escribirse

221221

1111112

10

ssss (3 – 45)

cuyo desarrollo nos muestra que es equivalente ala (3 – 44)

A menudo se emplea una notación abreviadapara escribir los determinantes de Slater. En lugar

de escribir y para las funciones de espín, sesuele poner una barra sobre la función espacialpara indicar la función de espín mientras que lafunción espacial sin barra indica que el factor deespín es .

Con esta notación abreviada el determinante(3 – 45) toma la forma

2121

11112

10

ssss

He

Como el determinante queda indicado por ladiagonal principal, la notación se simplifica aúnmás escribiendo los orbitales con su configura-ción de espín de la diagonal principal entre barras.Para el caso del helio se escribe

21110 ssHe

Para el átomo de litio la función se puede es-cribir

sssLi

2110

Debemos remarcar que las funciones i deldeterminante de Slater (3 - 43) dependen sola-mente de una coordenada electrónica (o sea de lascoordenadas correspondientes a una sola partícu-la, el electrón) y se denominan espín - orbitales.Estos espín - orbitales dependen de las tres coor-denadas espaciales y una coordenada de espín co-rrespondiente a un electrón. Cuando no se incluyeel espín estas coordenadas se llaman orbitales.

Problema:

6. Escriba la función de onda determinantalnormalizada de Slater para el berilio en su confi-guración 1s22s2

Solución:



106

La configuración puede escribirse

Be: 1s22s2 = 1s s1 2s s2

Para un sistema de n electrones debe cons-truirse un determinante de n × n con un factor denormalización (n!)–1/2

Como el berilio tiene n = 4 electrones

42322212

423222124131211141312111

41

ssssssssssssssss

!

3 - 8. Acoplamiento L - S en átomos polie-lectrónicos

En general, hay diversas posibilidades deasignar electrones a varios orbitales, particular-mente cuando se trata de un conjunto de orbitalesdegenerados. Los orbitales podrían considerarsecomo “cajas”. Cada orbital estaría conformadopor dos “cajas” correspondientes a los dos valoresdiferentes del espín electrónico. Esta es otra ma-nera de decir que cada orbital puede “contener”dos electrones en tanto que los valores de susmomentos magnéticos de espín (ms) sean diferen-tes. De esta manera cada “caja” viene descriptapor dos números cuánticos; my ms. El problemade disponer n electrones en un conjunto de r orbi-tales degenerados, es equivalente al de plantearcuántas maneras diferentes son posibles para dis-poner n objetos indistinguibles entre j cajas, don-de j podría ser igual a 2r. La solución viene dadapor la expresión:

Número de maneras = !nj!n!j

Ejemplo:

Hay 15 maneras diferentes de ubicar dos elec-trones en orbitales p ya que j = 6 y n = 2 de modoque 6!/(2! X 4!) = (6 x 5)/2 = 15

Problema:

7. ¿Cuántas maneras habrá de ubicar 6 electro-nes en un conjunto de orbitales f ?

Solución:

Como hay 7 orbitales f para cada valor de n y encada orbital puede haber dos electrones, el pro-blema se reduce a establecer de cuantas maneraspueden ordenarse 6 elementos idénticos en 14 po-siciones equivalentes. Por consiguiente

Número de maneras = !!!

614614

= 3003

Recordamos que para el hidrógeno, todos losorbitales con el mismo valor de n tienen la mismaenergía. Pero esto es sólo válido para el hidrógenoy los hidrogenoides. En átomos polielectrónicos,los orbitales con el mismo valor de n pueden tenerenergías diferentes. ¿Cómo podemos decidir cuál(o cuáles) de esas disposiciones corresponden alestado de menor energía? Para ello debemos ana-lizar como se acoplan entre sí los momentos an-gulares orbitales de los distintos electrones paraproducir un momento angular total. El proceso serepite para los momentos angulares de espín. Ladisposición que da la menor energía será aquellapara la cual el momento angular de espín tenga elvalor más alto y dentro de ese grupo la que tengael mayor momento angular orbital total. Esta dis-posición será consistente con el principio de ex-clusión de Pauli y lleva a establecer lo que se co-noce como la regla de máxima multiplicidad deHund.


El proceso es muy directo cuando interesa sólola distribución electrónica que corresponde al es-tado de menor energía, es decir, el estado funda-mental.

Ejemplo:

Si consideramos las distintas distribuciones po-sibles para 3 electrones en un conjunto de orbita-les d. Como hay 5 orbitales d para cada nivel deenergía, y cada uno de ellos admite dos electro-nes, habrá 10!/(3! X 7!) = 120 distribuciones dife-rentes. ¿Cuál de ellas corresponde al estado demenor energía?

Para ello le asignamos a cada orbital un valor deml y los representamos

____ ____ ____ ____ ____ml 2 1 0 -1 -2

El valor del espín total S surgirá de aquellacombinación de números cuánticos individualesms que tenga el valor máximo. Como ms puedetomar valores ½ o – ½, elegimos los tres valorespositivos, de modo que S = 3/2. El valor total de L,se obtiene de sumar los valores individuales de m

que nos dan el valor más alto, consistentes conque todos los electrones tengan el mismo espín.Esto se cumple ubicando un electrón en el orbitalpara el cual m=2 otro en el orbital para el cual m

=1 y el tercero en el orbital para el cual m= 0.

__X__ __X__ __X__ ____ ____m

2 1 0 -1 -2

Por lo tanto, L es igual a 3. Esta disposición demenor energía tiene S = 3/2 y L = 3. Cuando S es3/2 Ms, la proyección de S sobre el eje z puede ser3/2, ½ ,– ½ o 3/2. Esto es, hay 4 valores posiblespara Ms. En general, el número de valores posi-bles para Ms es 2S+1. Análogamente, cuando L =3 hay 2L + 1 valores posibles para M, la proyec-ción de L sobre el eje z. En nuestro caso, para 3electrones en orbitales d, habrá 2 × 3 + 1 = 7 valo-

res posibles para M. El número total de disposi-ciones que contribuyen al estado de menor energ-ía se obtiene multiplicando el número total de va-lores de Ms por el número total de valores deMen este caso

(2L+1) × (2S+1) = 7 × 4 = 28

Ese estado se describe mediante en símbolo

2S+1L

En esta notación el valor 2S + 1 se coloca comosuperíndice a la izquierda y, siguiendo la notaciónespectrográfica, el valor de L se representa me-diante una letra. Esas letras son

L 0 1 2 3 4 5 6 7 8letra S P D F G H I J K

De esta manera, el estado fundamental de nues-tro sistema se representa mediante el símbolo 4F

Problema:

8. ¿Qué información suministra el símbolo 1D2acerca del momento angular de un átomo?

Solución:

La letra D indica que L = 2. El superíndice 1es el valor de 2S + 1, o sea que S = 0 y el subíndi-ce 2 es el valor de J. Por lo tanto L = 2 S = 0 J= 2

En el caso que comentamos en el ejemplo ante-rior, 3 electrones en orbitales d (o d3), hay 120maneras de disponer esos 3 electrones en los 5orbitales d. Hemos visto que 28 de ellos contribu-yen al estado fundamental y, por lo tanto, todasestas configuraciones tienen que tener energía si-



108

milar. ¿Qué ocurre con el resto? Esas distribucio-nes corresponden a diversos estados excitados.

Lo que hemos visto hasta aquí, se llama esque-ma de acoplamiento, en particular hemos realiza-do el llamado acoplamiento L- S o de Russell -Saunders. Este esquema se usa para muchos ele-mentos, especialmente para los elementos con Z 40, pero no es estrictamente correcto para elemen-tos de números atómicos altos. Hemos acopladomomentos orbitales con momentos orbitales ymomentos de espín con momentos de espín. Dadoque ambos son momentos angulares, podemosconsiderar acoplarlos juntos en un llamado “aco-plamiento espín – órbita”. Esto se hace medianteel acoplamiento de L con S.

El momento angular electrónico total de unátomo ( J

) es el vector suma de los momentos

angulares orbital y de espín electrónicos totalesSLJ

. El operador Ĵ para el momento angu-lar electrónico total conmuta con el hamiltonianodel átomo de manera que se puede caracterizar unestado atómico mediante un nuevo número cuán-tico J. El acoplamiento es tal que los valores de Jvarían desde L + S, L + S-1, ... hasta L – S

En el ejemplo que estamos usando, los valoresposibles de J serían 9/2, 7/2, 5/2 y 3/2. Esos estadosse designan mediante la expresión general

2S+1LJ

El valor particular de esta expresión para unestado electrónico dado, se conoce como “símbo-lo de término” (term symbol, en inglés).

La cantidad 2S + 1 se llama multiplicidad deespín electrónico o, simplemente, multiplicidad.Si L S la multiplicidad de espín da el número deniveles que se originan en un término dado. ParaL< S los valores de J van desde S + L hasta S – Ly son, en total, 2L + 1.

Cuando los valores de 2S + 1 son 1, 2, 3, 4, 5,6, ..., se usan las palabras singlete, doblete, triple-te, cuartete, quintete, sextete, ... para designar la

multiplicad de espín. El símbolo 3P1 se lee “triple-te P uno”

Volviendo a nuestro ejemplo, los estados son4F9/2, 4F7/2, F5/2 y 4F3/2. La degeneración de cadaestado escrita de esta manera es 2J + 1. Estos es-tados tienen energías ligeramente diferentes. Elcálculo combinatorio permite demostrar que loscuatro estados 4F tienen degeneraciones 10, 8, 6 y4, esto es, las 28 configuraciones mencionadasanteriormente.

Para números atómicos bajos las diferenciasde energías entre estados con el mismo valor de2S + 1, es decir, con la misma multiplicidad, sepueden omitir. Pero esa diferencia entre ellos au-menta a medida que aumenta el número atómico.Para la mayoría de los propósitos, cuando se ana-lizan los elementos de la primera serie de transi-ción se suele ignorar la parte J del acoplamiento yse escribe el estado basal como 4F. Estudios másdetallados concluyen que si el conjunto de orbita-les tiene menos de la mitad de los electrones po-sibles, el menor valor de J da la menor energía ysi el número de electrones es más de la mitad delos que pueden admitir los orbitales, la menorenergía corresponde al mayor valor de J. En nues-tro ejemplo, el estado fundamental para el caso d3

sería aquel para el cual 4F3/2

Problemas:

9. Un grupo de términos relacionados tienenel símbolo de término común 2P

a) Cuáles son los símbolos completos paraeste multiplete?

b) En ausencia de campos magnéticos,¿Cuántos niveles de energía existen para este mul-tiplete?

Solución:

a) s = 1/22s+1 = S = 2


J = 1/2, 3/2

2P1/2 y 2P3/2

b) Para este multiplete existen 2 niveles deenergía

10. Establezca el símbolo para el estado ba-sal de cada uno de los siguientes átomos

a) Na (1s22s22p63s)

b) P (1s22s22p63s23p3)

c) Ne (1s22s22p6)

d) Ti (1s22s22p63s23p64s23d2)

Solución:

a) S = ½2S+1 = 2L = 0J = 1/22S1/2

b) S =½+ ½ +½= 3/2 2S+1 = 4L= 1 + 0 –1 = 0J = 3/24S3/2

c) S = 02S+1 = 1L = + 2 + 0 – 2 = 0J = 01S0

d) S = ½ + ½ = 12S+1 = 3L = 2 + 1 = 3J = 23F2

En el acoplamiento de Russell – Saunders sesupone que cada electrón en un átomo tiene

números cuánticos propios. En rigor, no es co-rrecto que en un átomo polielectrónico cadaelectrón tenga números cuánticos propios.

Dada la configuración electrónica de un áto-mo, habrá un conjunto de estados cuánticos cadauno de ellos caracterizado por L, S y J. J recibetambién el nombre de interacción espín - órbita(SO). Debemos destacar que la fuerza de esta in-teracción es mucho menor que la interacción elec-trostática electrón - núcleo.

Teniendo en cuenta la interacción espín –órbita, el hamiltoniano para un sistema de n elec-trones es

n

i

n

jiSO

ij

n

i ii H

re

rZe

mH

1

2

1

22

2

2

donde el primer término del segundo miembro serefiere a la interacción electrón - núcleo, el se-gundo término se refiere a las interaccioneselectrón - electrón y el tercero a la interacciónespín - órbita. El valor medio de SOH es una fun-ción de L, S y J.

SOH =(J, L, S)

La interacción espín - órbita es la responsabledel desdoblamiento de las rayas en la estructurafina del espectro, dando dobletes, tripletes o mul-tipletes. Así por ejemplo, en el espectro del sodioel doblete correspondiente a las rayas de 5890 Å y5896Å se debe al efecto del SOH

Existe otra manera de estimar la relación entrelas rayas espectrales y el acoplamiento espín orbi-ta de los electrones. Es el llamado acoplamiento j-j de electrones equivalentes o, simplementeacoplamiento j-j. En él se acoplan los valores dem y ms de cada electrón individual para dar elvalor correspondiente de ji. Luego, todos losvalores de los ji se acoplan para dar el valor de J.Este método se usa en los cálculos de Mecánica



110

do se usa en los cálculos de Mecánica Cuánticarelativista y da mejores resultados que el acopla-miento L – S cuando Z > 40.

La mayor parte de los núcleos atómicos tam-bién poseen espín, pero sus momentos magnéticosson muchísimos menores que los que correspon-den a los espines de los electrones. Esto se debe aque la masa del protón es casi 2000 veces mayorque la del electrón. Por esta razón, los camposmagnéticos nucleares son muy débiles.

Los campos magnéticos nucleares producenuna estructura fina en las líneas espectrales y se-paran aún más los niveles de energía atómicos. Laseparación de las líneas espectrales que generanlos núcleos y los electrones depende de las orien-taciones relativas entre los momentos magnéticosnucleares y los electrónicos, lo cual implica dife-rentes energías de interacción. El patrón de nive-les de energía que se obtiene, y las líneas espec-trales correspondientes, se llama estructurahiperfina.

3- 9. Regla de Hund (Máxima multiplicidad)

Se usa para determinar el estado de menorenergía entre los diversos términos que surgen deuna configuración electrónica.

1) El estado de mayor valor de S es el estadode menor energía. La energía aumenta amedida que S disminuye.

2) Para estados con el mismo valor de S, el es-tado con mayor valor de L es el que tiene elmenor valor de energía.

3) Para estados con los mismos valores de S yL si la subcapa tiene menos de la mitad delnúmero máximo de electrones, el estadocon menor valor de J es el de energía másbaja.

Con algunas excepciones, esta regla es válidapara las configuraciones de los estados basales delos átomos, pero no necesariamente se cumplepara estados excitados.

Como en un estado degenerado la máximamultiplicidad se alcanza cuando en cada uno deesos orbitales hay un electrón con ms = ½, la reglade Hund se suele expresar:

La distribución más estable de electronesen los subniveles es aquella que tenga mayornúmero de espines paralelos (+½)

Problema:

11. La configuración electrónica del catiónNi2+ es 1s2 2s2 2p6 3s2 3p6 3d8 ¿Cuáles son los va-lores posibles del número cuántico total de espínS? ¿Cuál es valor máximo de L? ¿Cómo se sim-boliza ese estado?

Solución:

La configuración electrónica del catión Ni2+ sepuede abreviar [Ar] 3d8. Todas las subcapas, ex-cepto la 3d están completas, es decir tienen todossus electrones apareados, y por lo tanto no tienenespín neto. Aplicando la Regla de Hund a loselectrones 3d se encuentra hay sólo dos electronesdesapareados, que podemos representar

Los electrones apareados del subnivel 3d nocontribuyen al espín total, por lo que solo debe-mos considerar los espines de los electrones céli-bes ms1 = ½ y ms2 = ½. Para adjudicar los valoresde S debemos partir de

S = (ms1 + ms2), … , (ms1 – ms2). Luego S = 1, 0

Consideramos que hay dos electrones en elorbital para el cual m = 2, dos electrones en el


orbital para el cual m = 1, dos electrones en elorbital para el cual m = 0, un electrón en el orbi-tal para el cual m = -1 y un electrón en el orbitalpara el cual m = -2. Por lo tanto el valor total deL será 4 + 2 + 0 – 1 – 2 = 3

En este ejemplo los dos espines de los electro-nes célibes son ½. Por lo tanto S = 1 y

J = L + S = 4.

El símbolo para este estado será:

3F4

3 - 10. Regla del Aufbau

Imaginemos un experimento hipotético en elcual tenemos un núcleo con Z protones y N neu-trones y, mediante algún artificio, le agregamosuno a uno Z electrones hasta obtener un átomoneutro. Como es un principio aceptado que todosistema tiende espontáneamente hacia el estado demenor energía compatible con las condicioneslimitantes, a medida que los vamos agregando, loselectrones tienden a adquirir la configuración quehaga mínima la energía del átomo. En ese proce-so, el primer electrón ocuparía el nivel energético1s. El segundo electrón ocuparía también ese ni-vel a condición que su espín sea opuesto al quetiene el primer electrón tal como lo establece elPrincipio de exclusión de Pauli. Colmada la capa-cidad del nivel energético para el cual n = 1, elelectrón siguiente ocuparía el nivel 2s, el cuartotambién pero con espín opuesto. Hay 3 orbitales2p degenerados. La regla de Hund nos dice que elestado de menor energía es el que corresponde almayor valor de S, por lo tanto los primeros 3 elec-trones que incorporemos ocuparán cada uno deellos un orbital 2p distinto y todos tendrán ms = ½.

Una vez que están todos los orbitales “ocupados”,cada uno por un electrón, los siguientes 3 electro-nes se irán apareando con espín – ½.

La evidencia experimental corrobora la reglade Hund. El oxígeno (Z = 8) tiene 8 electrones,cuya configuración podemos escribir 1s2 2s2 2p4.Si los cuatro electrones 2p estuvieran apareadosen dos orbitales, el momento magnético de espíndel átomo sería nulo. Sin embargo, los átomos deoxígeno tienen comportamiento paramagnético loque revela que, aún en el estado fundamental, tie-nen electrones desapareados. Esto se explica so-bre la base de la regla de Hund asignando la si-guiente configuración: 1s2 2s2 2px

2 2py1 2pz

1 conlos espines +½ en los orbitales 2py y 2pz

3 – 11. Configuración electrónica y TablaPeriódica

Entre fines de la década de 1920 y principiosde la siguiente, los métodos aproximados para es-tablecer configuraciones electrónicas permitieroncorrelacionar estas configuraciones con el orde-namiento empírico de los elementos según suspropiedades físicas y químicas, que habían des-arrollado en el siglo anterior Dimitri IvanovichMendelejeff y Julios Lothar Mayer.

Los métodos empleados inicialmenteconsistían en escribir una función de ondaaproximada que le asignaba electrones a espín-orbitales hidrogenoides. En cada orbital, la carganuclear era sustituida por un parámetro variacio-nal que representa una carga nuclear efectiva Zefectque daba cuenta del apantallamiento electrónico.Para satisfacer el principio de Pauli, la función deonda se escribía como un determinante de Slater.Para algunos estados atómicos, la función de ondatuvo que escribirse como una combinación linealde varios determinantes de Slater.

Como un electrón tiene dos posibles estadosde espín ( o ), el principio de exclusión requie-



112

re que no haya más de dos electrones que ocupenel mismo orbital en un átomo o molécula. Doselectrones en el mismo orbital deben tener espinesantiparalelos, (se dice que los electrones estánapareados). Un conjunto de orbitales con el mis-mo valor n y el mismo valor de constituye unasubcapa. Las subcapas más bajas son 1s, 2s, 2p,

3s,... Una subcapa s tiene = 0 y m = 0, por loque sólo puede contener como máximo dos elec-trones sin violar el principio de exclusión. Unasubcapa p tiene = 1 y tres valores posibles dem: -1, 0, +1; por eso una subcapa p puede conte-ner hasta 6 electrones; las subcapas d y f tienenuna capacidad máxima de 10 y 14 electrones, res-pectivamente.

La fórmula para la energía de un átomo hidro-genoide puede modificarse para aproximar, deuna forma grosera, la energía E de un orbital ató-mico dado como

eV,n

ZE efect 6132

2

donde n es el número cuántico principal y la carganuclear efectiva Zefect es diferente para las distin-tas subcapas en el mismo átomo. Se suele expre-sar Zefect = Z - s, donde Z es el número atómico y ses la constante de apantallamiento para una sub-capa determinada que es la suma de las contribu-ciones electrostáticas de los otros electrones pre-sentes en el átomo.

En 1955, Richard Latter6 calculó las energíasorbitales aproximadas para los átomos de los ele-mentos en el orden creciente de su ordenación enla Tabla Periódica, reemplazando un cálculo muycomplicado del método Hartree – Fock por unafunción sencilla obtenida a partir del método deThomas – Fermi – Dirac, un método que utilizalas ideas de la Mecánica Estadística para obtener

6 Phys. Rew.99, 510 (1955)

aproximaciones a las funciones de energía poten-cial efectivas para el electrón, así como para cal-cular la densidad de probabilidad electrónica enun átomo. En la Figura 3 – 3, se representan lasenergías orbitales calculadas por Latter para losestados fundamentales de los átomos neutros.

Figura 3 – 3.- Energías de los orbitales atómi-cos en función de Z para átomos neutros en estadofundamental, en escala logarítmica. Expresada porM. Kasha a partir del trabajo de R. Latter. (EH = -13,6 eV)

Las energías de los orbitales atómicos calcu-ladas por Latter concuerdan bastante bien tantocon las calculadas por el método Hartree – Fockcomo con los resultados experimentales.

Las energías orbitales cambian con el númeroatómico Z. Al aumentar Z la energía del orbitaldisminuye debido al aumento de la atracción entre


el núcleo y los electrones. Esta disminución esmucho más marcada para los orbitales internos.

Para el hidrógeno y los iones hidrogenoides,todos los orbitales con el mismo valor del númerocuántico n tienen la misma energía. Pero para Z >1, los orbitales con el mismo número cuántico npero con distinto valor de tienen distintaenergía. Por ejemplo, cuando n = 3 se encuentraque E3s < E3p < E3d. Mientras que en el átomo dehidrógeno estos niveles están triplemente degene-rados, en los átomos con Z > 1, se produce undesdoblamiento debido a las repulsiones inter-electrónicas. Sin embargo, cuando Z es muygrande los orbitales con el mismo valor de n tien-den a estar degenerados, debido a que las repul-siones interelectrónicas son despreciables frente ala atracción nuclear que experimentan esos elec-trones.

En las ordenadas de la Figura 3 – 3, se repre-senta la raíz cuadrada de la energía relativa de unátomo respecto a la del hidrógeno. Debido a quela carga nuclear Zefect para los electrones 1s delneón (Z = 10) es casi 10 veces mayor que la delelectrón 1s del hidrógeno, la energía E1s del orbi-tal 1s para el Ne es — en valor absoluto —aproximadamente 100 veces la energía E1s del H.

Para la mayor parte de los valores de Z, losorbitales 3s y 3p están mucho más próximos entresí que los orbitales 3p y 3d, lo que “explica” laestabilidad de configuraciones ns2 np6, donde lossuperíndices indican el número de electrones encada subcapa, sobreentendiéndose cuado el super-índice es 1. Se observa también que la relaciónentre las energías de algunos orbitales cambia conZ. En el átomo de hidrógeno, el orbital 3d tienemenor energía que el 4s, pero para valores de Zcomprendidos entre 7 y 20 el orbital 4s tiene me-nor energía que el 3d. En cambio, para valoresgrandes de Z el orbital 3d tiene menor energía queel 4s.

La configuración del estado fundamental delLi es 1s2 2s. Puede esperarse que el Li pierda

fácilmente un electrón (el electrón 2s tiene muchomenor energía) para formar el ion Li+, y este es elcomportamiento químico observado.

Las configuraciones de los estados fundamentalesdel berilio y del boro son 4Be: 1s22s2 y 5B:1s22s22p. Para el carbono, la configuración delestado fundamental es 6C: 1s22s22p2. En la Sec-ción 3 – 8 se vio que, para estados degenerados,son posibles diversas configuraciones electróni-cas. Para el estado fundamental del carbono(1s22s22p2), la regla de Hund nos dice que eltérmino más bajo tendrá los dos espines 2p para-lelos:

La ubicación de los dos electrones 2p en orbi-tales diferentes minimiza la repulsión electrostáti-ca entre ellos. La subcapa 2p se completa en el10Ne, cuya configuración electrónica es 1s22s22p6

Al igual que el helio, el neón no forma compues-tos químicos estables.

La configuración del sodio en el estado fun-damental es 1s22s22p63s, y sus propiedades físicasy químicas se asemejan a las de su predecesor enel grupo 1 de la tabla periódica: el Li (cuya confi-guración del estado fundamental es 1s22s). De es-ta manera, la ordenación de los elementos en latabla periódica resulta ser una consecuencia de laforma y ordenación de los orbitales hidrogenoi-des, de los números cuánticos permitidos y delprincipio de exclusión.

El tercer período termina con el Ar, cuya con-figuración del estado fundamental es1s22s22p63s23p6 y que, por comparación con la delneón puede escribirse [Ne] 3s23p6.



114

Para el potasio (Z = 19) el orbital 4s tiene me-nor energía que el 3d. (Figura 3 – 3). Por ello, laconfiguración electrónica del nivel fundamentaldel 19K es 1s2 2s2 2p6 3s2 3p6 4s. De manera simi-lar al potasio, en el estado fundamental del átomode calcio la subcapa 4s cae por debajo de la 3d yla configuración electrónica basal del 20Ca es1s22s22p63s23p64s2. La subcapa 3d comienza allenarse, para Z = 21, dando la primera serie delos elementos de transición. En el estado funda-mental del cinc, la subcapa 3d se completa con 10electrones y la configuración electrónica del 30Znes [Ar]3d104s2 — el nivel energético 3d es ahoramás bajo que el 4s. El cuarto período se completacon el criptón cuya configuración electrónica ba-sal es [Ar] 3d104s24p6.

Las tierras raras (lantánidos) y actínidos en losperíodos sexto y séptimo corresponden al llenadode las subcapas 4f y 5f.

El orden de llenado de las subcapas en la tablaperiódica viene dado por la regla n + : las subca-pas se llenan en orden creciente a los valores n +; para subcapas con los mismos valores de n + el que tiene el n más bajo se llena primero.

Niels Bohr fue quien racionalizó la tabla periódicaen términos de ocupación de los niveles de energ-ía atómicos, y la forma familiar de la tabla perió-dica larga se debe a él.

Para un análisis más profundo sobre la confi-guración electrónica de los átomos e iones de losmetales de transición, pueden verse L. G. Van-quickenborne et al, J. Chem. Educ, 71, 469(1994); Levine (2000), sec. 11.2.

3 – 12. El método del campo autoconsisten-te de Hartree – Fock

Para describir explícitamente el movimientode cada electrón y sus interacciones de Coulombcon todas las demás partículas cargadas eléctri-

camente presentes en el sistema que se estudia,siempre puede escribirse un operador mecánicocuántico hamiltoniano “exacto”. Sin embargo, lafunción de onda correspondiente sólo puede obte-nerse con exactitud para el átomo de hidrógeno.Con una excelente aproximación se obtienen lasfunciones de onda para átomos hidrogenoides.Mediante procedimientos variacionales se hancalculado funciones de onda con muy buenasaproximaciones para los átomos de helio y de li-tio. Para átomos con número atómico elevado, omoléculas sencillas, el método de Hartree - Focksuministra la aproximación más simple posiblepara obtener funciones de onda. A partir delmétodo original desarrollado por Douglas RaynerHartree en 1928 y mejorado por VladimirAlexandrovich Fock en 1930, se han propuestouna variedad de maneras de obtener funciones deonda aproximadas a partir de un hamiltonianoexacto para especies polielectrónicas. Esos méto-dos se conocen genéricamente como “métodosHartree – Fock”, son “ab initio” y se usan am-pliamente en Química Cuántica.

Para explicar estos métodos supondremos quetenemos un átomo polielectrónico neutro, Z = n,cuyo núcleo tiene una masa infinitamente mayorque los electrones. El hamiltoniano para ese áto-mo será del tipo

n

i ij ij

n

i i

n

ii r

er

Zem

H1

2

1

2

1

22

2

(3 – 46)

En este hamiltoniano tenemos tres sumatorias. Laprimera contiene los operadores para la energíacinética de los n electrones, la segunda expresa laenergía potencial resultante de las atracciones en-tre los electrones y el núcleo de carga y la terceraexpresa la energía potencial resultante de las re-pulsiones interelectrónicas (usamos la restricciónj > i, que impide tomar en cuenta dos veces lamisma repulsión interelectrónica). Precisamentees este último término el que impide la resoluciónexacta de la ecuación de Schrödinger. Si despre-ciamos este término, la ecuación podría separarseen n ecuaciones de un electrón hidrogenoide para


obtener una función de onda de orden cero comoproducto de n orbitales (de un electrón) hidroge-noides.

),,r(),,r(),,r( nnnn)( fff 22221111

0

(3 – 47)

donde los orbitales hidrogenoides son

,YrR mm

f (3 – 48)

Si en cada uno de los orbitales incluyésemosdos electrones de espín opuesto, siguiendo elprincipio de exclusión de Pauli, obtendríamos laconfiguración del estado fundamental.

La función de onda aproximada (3 – 47) tienecierta utilidad cualitativa pero deja mucho quedesear en cuanto a su precisión cuantitativa, entreotras causas debido a que para el cálculo de todoslos orbitales se considera la carga nuclear total Z.Una manera de lograr una mejor aproximaciónconsiste en emplear diferentes números atómicosefectivos para los distintos orbitales teniendo encuenta el efecto de apantallamiento de los electro-nes. Si bien el empleo de números atómicos efec-tivos produce una considerable mejora, la funciónde onda dista todavía bastante de ser precisa yaque se está despreciando los efectos de la repul-sión entre los electrones.

La siguiente etapa consiste en elegir una fun-ción variacional que tenga la misma forma que la(3 - 47) pero que no esté restringida al uso de or-bitales hidrogenoides o de ninguna otra formaparticular. La manera usual consiste en proponeruna función de onda del tipo

nnnn ,,rg,,rg,,rg 22221111

(3 – 49)

y tratar de encontrar las funciones g1, g2, ...gn queminimizan la integral variacional

d*

dH*

En el método variacional más simple se esco-ge una función de prueba que incluye variosparámetros y se van modificando esos parámetrospara tratar de encontrar un valor teórico de laenergía que se aproxime cada vez más al valorexperimental. En este caso deben variarse las fun-ciones gi para minimizar la integral variacional.Así y todo, la ecuación (3 - 49) será siempre unaecuación aproximada. A diferencia del caso delátomo de hidrógeno, la ecuación de Schrödingerno es separable, de modo que la verdadera fun-ción de onda no puede escribirse como productode n funciones de un electrón.

Calcular las funciones de onda (3 - 49) para unátomo polielectrónico es una tarea muy complica-da. Por ello se simplifica aproximando los mejo-res orbitales posibles por medio de orbitales queson el producto de un factor radial, hi(ri) por unarmónico esférico, ii

m ,Y

iim

iii ,Yrhg

(3 – 50)

Esta aproximación es la que generalmente seemplea en cálculos atómicos.

El procedimiento para el cálculo de gi fue in-troducido inicialmente en forma casi intuitiva porHartree en 1928, y recibe el nombre de métododel campo autoconsistente (abreviado SCF, porself-consistent-field). La demostración de que elmétodo de Hartree da la mejor función de varia-ción de la forma (3 - 49) fue realizada por Fock ySlater en 1930 quienes introdujeron en el métodode Hartree la restricción del Principio de Exclu-sión.

El procedimiento de Hartree consiste es-quemáticamente en lo siguiente:



116

Se plantea una función de onda, 0, que tengala forma de producto de n funciones normalizadascorrespondientes a los n electrones

nnnn ,,rs,,rs,,rs 222211110

(3 – 51)

cada si es del tipo de la (3 – 50), es decir, es unafunción normalizada de r multiplicada por unarmónico esférico. En una primera etapa se elige0 como producto de n orbitales hidrogenoidescon números atómicos efectivos Zefect.

Luego se analiza el comportamiento de cadaelectrón considerando que los demás tienen unadistribución uniforme y fija. Así, por ejemplo, pa-ra el electrón 1 se considera que los electrones 2,3, ..., n forman una distribución estática de cargaeléctrica a través de la cual se mueve el dichoelectrón 1, con lo que se está promediando las in-teracciones instantáneas entre el electrón 1 y losdemás electrones.

La energía potencial entre dos cargas puntua-les q1 y q2 está dada por

21

2121

,, r

qqU

Sea q1 = - e1 y q2 la carga de los electrones 2,3, ..., n que presentan una distribución continuade carga. Llamando 2 a la densidad de la cargaq2, la carga infinitesimal dq2 en un volumen d2será 2 d2.

La carga q2 puede escribirse

222 dq

Por lo tanto, la interacción entre la carga q1(=-e1) y la carga q2 hace que la energía potencial sea

221

2121

d

rqU

,, (3 – 52)

Para la función (3 - 51) la densidad de proba-bilidad del electrón i es si2. Por lo tanto, para elelectrón 2 (con carga - e) la densidad de carga dela nube de carga hipotética es

222 se (3 – 53)

y la energía potencial será

221

222

21 drs

eU,

, (3 – 54)

Sumando las interacciones con los otros electro-nes se tiene

n

jj

j,

jn,,, d

rs

eUUU2 1

2

213121 (3 – 55)

La energía potencial de la interacción entre elelectrón 1 y los otros electrones y el núcleo será

1

2

2 1

2

2111 r

Zedrs

e,,rUn

jj

j,

j

(3 – 56)

Además de considerar a la función de onda 0como producto de orbitales de un solo electrón sehace una nueva aproximación consistente en con-siderar que el potencial efectivo que actúa sobreun electrón en un átomo polielectrónico es sólofunción de r. Para ello se promedia 111 ,,rUpara los ángulos y se encuentra una expresión dela energía potencial que sólo depende de r1. Estaexpresión es del tipo


ddsen

ddsenrUrU 2

0

2

0

111

2

0

2

0111

1

,,

(3 – 57)

De este modo U(r1) se puede introducir comoenergía potencial en una ecuación de Schrödingerde un solo electrón:

112 1111

21

2

ttrUm

(3 – 58)

de la que se obtiene t1(1) que es un orbital mejo-rado para el electrón 1. 1es la energía delelectrón 1 (aproximada, en esta etapa). Como laenergía potencial dada por la (3 – 57) tiene si-metría esférica, el factor angular de t1(1) es unarmónico esférico que implica los números 1 ym1. Se obtiene un conjunto de soluciones R(r1)que corresponden a todos los posibles valores de1 entre los valores límites de r1 (0 y ). Del con-junto de soluciones R(r1) elegimos la que corres-ponde al orbital que estamos tratando. Si electrón1 es un electrón 1s de la configuración 1s2 2s2 2pdel boro, U(r1) se calcula a partir de un electrón1s dos electrones 2s y un electrón 2p y mediantela (3 – 49) se obtiene un orbital 1s mejorado.

Estimada t1(1) se procede a buscar un orbitalmejorado para el electrón 2. A este electrón se loconsidera como moviéndose en una nube de cargade densidad producida por los demás electrones

224

23

21 431 nsssre n

Se calcula la energía potencial efectiva U(r2)para el electrón 2 como en el caso del electrón 1 yse resuelve la ecuación de Schrödinger como en elcaso anterior. Se obtiene así otro orbital mejoradot2(2). Se continúa este proceso hasta tener una se-rie de orbitales mejorados para los n electrones.Logrado esto se vuelve al electrón 1 y se repite elproceso obteniéndose una nueva serie de orbitalesmejorados. El proceso se repite hasta que entre

dos iteraciones sucesivas no se obtengan cambios.El conjunto final de orbitales da las funciones deonda autoconsistentes de Hartree.

Como en el cálculo de i se incluye la energíapotencial debida a la repulsión electrónica, la itendría en cuenta cada repulsión electrónica dosveces. Es por ello que para evitar esta duplica-ción, al calcular la energía total E se le resta a lasumatoria de las i un factor que representa a lamitad de las energías debidas a la interaccionesinterelectrónicas. Se puede deducir que la expre-sión de la energía total es del tipo

ji

n

i ij ij

jin

ii dd

rjgige

E 1

222

1

(3 – 59)

Las integrales del segundo miembro de la (3 –59) se llaman integrales de Coulomb y se las sue-le representar mediante el símbolo Jij, de modoque la ecuación anterior puede escribirse

n

i ijij

n

ii JE

11

(3 – 60)

De esta manera, mediante el método de Har-tree se pueden establecer los orbitales, esto es lasfunciones espaciales, para los electrones de unátomo polielectrónico o de una molécula con muybuena precisión.

El conjunto de orbitales que tienen el mismonúmero cuántico principal constituye una capa.Las capas con n = 1, 2, 3, ..., se corresponden conlas capas espectroscópicas K, L, M, ...

Todos los orbitales que tienen el mismo par ny constituyen una subcapa. Los orbitales de unasubcapa diferirán en los valores de m.

Hemos dicho que los orbitales espaciales deHartree se pueden escribir como el producto de un



118

factor radial, hi(ri) por un armónico esférico, ii

ml ,Y

iim

iii ,Yrhg

(3 – 50)

Por lo tanto, si sumamos las densidades deprobabilidad de Hartree para los electrones de unasubcapa completa

mn

mn ,Yrh,Yrh mm 2222 22

(3 – 61)

El factor 2 que se incluye en la (3 – 61) se de-be a que puede haber dos electrones en cada orbi-tal. Eugen Merzbacher demostró que la sumatoriadel segundo miembro es igual a (2+1)/4Demodo que la suma de las densidades de probabili-dad

412

2rh ,n

es independiente de y de Esto implica que

Una capa cerrada tiene una densidad deprobabilidad de simetría esférica

Este enunciado se conoce como teorema deUnsöld. Si se trata de una capa semicompleta seomite el factor 2 en la (3 – 61). Se puede demos-trar que si la capa contiene la mitad del máximode electrones, su densidad de probabilidad tienetambién simetría esférica.

El tratamiento original de Hartree solo con-templaba las funciones espaciales. Aunque respe-taba un máximo de dos electrones por cada orbitalno contenía ninguna referencia explícita a la nece-sidad de que las funciones sean antisimétricas pa-ra el intercambio de electrones. En 1930 Fock ySlater perfeccionaron el método de Hartree em-pleando orbitales espín en lugar de orbitales espa-ciales. Los métodos del campo autoconsistente

que emplean una combinación lineal antisimétricade funciones espín - orbita y funciones espacialesreciben el nombre de cálculos Hartree – Fock. Laantisimetría que se requiere la proveen los deter-minantes de Slater de espín – órbita.

Las ecuaciones diferenciales para calcular losorbitales Hartree – Fock tienen la forma general

n,,,,iH iiiefecti 321 ff (3 – 62)

fi es el espín - orbital correspondiente alelectrón i, el operador efect

iH es el hamiltonianoefectivo para el electrón i y el valor propio i es laenergía orbital del electrón i. Debemos hacer no-tar que el hamiltoniano efectivo de Hartree – Fockcontiene términos adicionales al de Hartree debi-do a que contempla el intercambio de electrones.

A partir de 1950, los orbitales Hartree – Fockse representan como combinaciones lineales de unconjunto completo de funciones conocidas, lla-madas funciones base. Así, los orbitales espacia-les para el átomo de Li se escriben de la forma:

i

iii

ii cgbf

(3 – 63)

donde las i son ciertos conjuntos completos defunciones, mientras que b y c son los coeficientesdel desarrollo a determinar por el método delcampo autoconsistente.

El conjunto de funciones base que se empleacon más frecuencia es un conjunto de orbitales detipo Slater (STO) cuya forma normalizada es

,Yer!n

a/ ma/rn/

/n

01

21

210

22

(3 –64)

El conjunto de todas estas funciones para losque n, y m son enteros y todos los valores deson positivos constituye un conjunto completo.


El parámetro recibe el nombre de exponente or-bital.

En el desarrollo de (3 –63) se incluye unnúmero apropiado de orbitales de tipo (3 – 64)hasta obtener un orbital Hartree –Fock que dé va-lores próximos a los resultados experimentales.

Los métodos Hartree – Fock permiten predecirla los valores de la energía total en función de lageometría de los sistemas a las que son aplicables,- átomos polielectrónicos, grupos atómicos,pequeñas moléculas7 inorgánicas u orgánicas, loque permite encontrar los estados energéticos detransición, así como el cálculo de los espectrosvibracionales. Permiten establecer la distribuciónde cargas, frecuencias de infrarrojo, polarizacio-nes e interpretar espectros NMR. También se usanpara interpretar espectros de fotoemisión (aunquesólo de manera semicuantitativa).

Para sistema en los que son aplicables losmétodos Hartree – Fock se predicen las longitu-des de enlace con un error de ±0.03 Å y los ángu-los de enlace con una diferencia de unos pocosgrados. Pero las energías estimadas están casisiempre por debajo de los valores reales. Así, parael helio, el uso de un orbital hidrogenoide 1s me-diante el método de Hartree Fock, da una energíadel estado fundamental de – 77,9 eV, mientras queel valor verdadero es - 79,0 eV. Este error de 1,1eV se llama, usualmente, energía de correlacióny, al igual que en otras energías calculadas me-diante el método de Hartree - Fock, se debe a queno se tiene en cuenta las correlaciones instantáne-as en el movimiento de los electrones. Debido asus cargas eléctricas, los electrones se repelenmutuamente y correlacionan sus movimientos pa-ra evitar sus proximidades relativas. Este fenóme-no se denomina correlación electrónica.

7 Para ciertas moléculas como F2, O3, nitrocompuestosorgánicos, los métodos Hartree – Fock no dan resultadossatisfactorios

3- 13.- Interacción de configuraciones.

El método más común utilizado para mejoraruna función de onda de Hartree-Fock es la inter-acción de configuración. Al calcular la función deonda Hartree-Fock para el estado fundamental deun átomo o molécula, se obtienen tambiénexpresiones para los orbitales de estadosexcitados no ocupados. Se puede demostrar que elconjunto de funciones obtenidas haciendo todaslas asignaciones posibles de electrones a losorbitales disponibles constituye un conjuntocompleto. Por lo tanto, la función de ondaverdadera Y correspondiente al estadofundamental puede expresarse como

j

j,orbja YY (3 – 65)

donde Yorb,j son las funciones de onda orbitalesaproximadas que difieren entre sí en la asignaciónde los electrones a los orbitales. Cada Yorb,j es undeterminante de espín-orbital de Slater. Las fun-ciones Yorb,j se suelen llamar funciones de confi-guración. Para encontrar los valores de los coefi-cientes aj debe utilizarse un procedimiento varia-cional que minimiza la integral variacional; estetipo de cálculo se llama interacción de configura-ción (CI).

Para el estado fundamental del helio, el térmi-no con el mayor coeficiente en la función de ondaCI será un determinante de Slater con los doselectrones en los orbitales análogos a los 1s, perotambién contribuirán a la función los determinan-tes de Slater con electrones en los orbitales 2s, 2py de mayor energía. Una función de onda CI parael estado fundamental del átomo de helio tiene laforma

Y = a1Y(1s2) + a2Y(1s2s) + a3Y(1s3s) + a4Y(2s2) + + a5Y(2p2) + a6Y(2s3s) + a7Y(3s2) + …

donde los aj son coeficientes numéricos y unafunción del tipo Y(1s2s) indica un determinante



120

de Slater con un electrón en un orbital tipo 1s yotro en un orbital tipo 2s.

Los cálculos CI son extremadamente compli-cados ya que, a menudo, requieren combinacioneslineales de miles o incluso millones de funcionesde estado de configuración para obtener una re-presentación precisa de Y.

Problemas propuestos

3.1. Calcular la carga nuclear efectiva para unelectrón 2p del nitrógeno.

3.2. La energía de primera ionización del Li es5,39 eV. Estime la carga nuclear efectiva para elelectrón de valencia del Li.

3.3. Suponga que el potencial en una caja uni-dimensional en la que se mueve una partícula noes cero sino que es U=bx con b = constante. Cal-cular el efecto sobre la energía de la partícula, su-poniendo que ese potencial actúa como una pe-queña perturbación.

3.4. Calcule la energía de un oscilador armó-nico cuando es sometido a la pequeña perturba-ción de un potencial U = axk, donde a es unaconstante y (a) k es 3: (b) k es 4.

3.5. Escriba la función de onda determinantalnormalizada de Slater para el litio en su configu-ración 1s2 2s1

3.6. Escriba los símbolos de términos para lasconfiguraciones del Na y del F en sus estadosfundamentales y del C en su configuración exci-tada 1s2 2s2 2p1 3p1

3.7. ¿Qué información suministra el símbolo2F2 acerca del momento angular de un átomo?

3.8. ¿Cuáles de las siguientes transicionesestán permitidas en el espectro de emisión normalde un átomo: (a) 2s 1s (b) 2p 1s (c) 3d 2p (e) 4s 4p? Halladas las transiciones permi-tidas , escriba los símbolos espectrográficos de delos respectivos estados.

3.9. ¿Cuántos electrones pueden ocupar los si-guientes subniveles de energía: (a) 3s (b) 5d (c) 6f(d) 6h?

Las Páginas de Ruben Labato - III. `TOMOS POLIELECTRÓNICOS · 2013-06-17 · es la estimación de...

Documents

Transcript of Las Páginas de Ruben Labato - III. `TOMOS POLIELECTRÓNICOS · 2013-06-17 · es la estimación de...