Fractales - Manuel Alfaro A, Manuel Murrilo T. , Alberto Soto A..pdf

7/22/2019 Fractales - Manuel Alfaro A, Manuel Murrilo T. , Alberto Soto A..pdf

1/94

Revista Digital Matemtica Educacin e Internet (www.cidse.itcr.ac.cr/revistamate)

Alberto Soto A.

Instituto Tecnolgico de Costa Rica, 2010

ractales

Manuel Alfaro A.

Manuel Murillo T.


2/94

FRACTALES

Manuel Alfaro A.Escuela de MatemticaInstituto Tecnolgico de Costa Rica.

Manuel Murillo T.Escuela de MatemticaInstituto Tecnolgico de Costa RicaUniversidad Estatal a Distancia.

Alberto Soto A.Escuela de MatemticaUniversidad Estatal a Distancia.


3/94

ii

Derechos Reservados cPrimera Edicin.Revista digital, Matemtica, Educacin e Internet (www.cidse.itcr.ac.cr/revistamate/), 2010.Correo Electrnico: [email protected] de MatemticaInstituto Tecnolgico de Costa RicaApdo. 159-7050, CartagoTelfono (506)25502225Fax (506)25502493

Manuel Alfaro A.,Fractales / Manuel Alfaro A., Manuel Murillo T. y Alberto Soto A. 1 ed. Escuela de Matemtica,Instituto Tecnolgico de Costa Rica. 2010.

82 p.ISBN 978-9968-641-03-61. Fractal 2. Atractor 3. Grafos 4. Espacios mtricos 5. Medida Hausdorff 6. Enteros gaussianos7.Dimensin 8. Conjuntos de Cantor 9. Dimensin fractal 10. Dimensin topolgica

Lmite de responsabilidad y exencinde garanta: El autor o los autores han hecho su mejor esfuerzo en la preparacin de este material. Estaedicin se proporciona tal cual. Se distribuye gratuitamente con la esperanza de que sea til, pero sin ninguna garanta expresa o implcitarespecto a la exactitud o completitud del contenido.

La Revista digital Matemticas, Educacin e Internet es una publicacin electrnica. El material publicado en ella expresa la opinin de susautores y no necesariamente la opinin de la revista ni la del Instituto Tecnolgico de Costa Rica.

Este libro se distribuye bajo la licencia: Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. Esta licencia per-mite copiado y distribucin gratuita, pero no permite venta ni modificaciones de este material.Verhttp://creativecommons.org/about/licenses/.
http://localhost/var/www/apps/conversion/tmp/scratch_3/[email protected]://creativecommons.org/about/licenses/http://creativecommons.org/about/licenses/http://creativecommons.org/about/licenses/http://localhost/var/www/apps/conversion/tmp/scratch_3/[email protected]


4/94

Prefacio

Esta obra est dirigida, principalmente, a estudiantes de Matemtica y de Computacin, sin em-bargo, est dirigida tambin a todas aquellas personas que encuentran en las matemticas el lengua-je universal con el cual se pueden explicar los fenmenos en nuestro entorno y, por supuesto, atodos los que ven en ella una puerta que los llevar hacia la bsqueda del conocimiento orientadoal desarrollo cientfico y tecnolgico.Se pretende introducir, con un nivel intermedio, el tema de los fractales. Nos interesa rescatar sudesarrollo matemtico: topologa, teora de la medida y geometra, sin olvidar la parte visual y lashermosas imgenes generadas por computadora que tienen estos conjuntos.Los fractales constituyen un tema matemtico de actualidad y se han convertido en algo muypopular en los ltimos aos. Las figuras fractales se obtienen de repetir una y otra vez el mismoprocedimiento, en forma recursiva o bien iterada, tpicamente un fractal es algo irregular, pero loms importante es que si lo ampliamos arbitrariamente, l an sigue irregular.Para nosotros, los fractales sern en general figuras geomtricas que se caracterizan por su autose-mejanza sin embargo existen otros, como la frontera del conjunto de Mandelbrot, que son fractalesno autosemejantes. Son estructuras infinitas contenidas en una superficie finita y resultan de util-idad en el anlisis de una gran diversidad de fenmenos como turbulencias, bolsa de valores,dispersin del humo, etc., adems de sintetizar imgenes como montaas, nubes, costas rocosas,ros y plantas entre otras.En el Captulo1se introducen los sistemas iterados de funciones y se muestran algunos ejemplosde sus atractores como el conjunto de Cantor, el tringulo de Sierpinski y el dragn de Heighway yse define la dimensin de semejanza. Tambin formaliza propiedades de estos conjuntos y detallesimportantes.En el Captulo2se representan nmeros complejos usando bases complejas, se discute sobre bue-

nas" bases y malas" bases. Se obtienen las figuras de conjuntos de fracciones de nmeros repre-sentables en estas bases y se describen propiedades topolgicas de ellos.En el Captulo3se define las dimensiones topolgica y Hausdorff, cuando la dimensin topolgicaes menor se define un fractal en el sentido original de Mandelbrot. Se trabaja con ejemplos de cmocalcular las dimensiones involucradas. Se exhiben otros tipos de dimensin fractal y se notan lassimilitudes que hay entre ellas.En el Captulo4se presentan algunas aplicaciones interesantes, como son la compresin de im-genes, los dilemas espaciales de evolucin, as como el crecimiento fractal y el modelo D.L.A.En el ApndiceAse presentan algunos de los programas computacionales que se han utilizadopara implementar los algoritmos dados y generar las figuras o grficos que se presentan.Finalmente, la bibliografa es extensa y los libros, artculos as como los dominios en internet quese incluyen, le puede servir a los lectores para profundizar en los temas aqu tratados.

M. ALFARO, M. MURILLO, A. SOTO

San Jos, Costa Rica

2008

iii


5/94

Lista de Smbolos

(S,), (T, ), . . . denotan espacios mtricos(r1, r2, . . . , rn) lista de razones(f1, f2, . . . ,fn) lista de semejanzas

Nr(A) r-vecindario deAL(A) medida de Aen el sentido de Lebesgue

C conjunto de Cantor clsico otros conjuntos de Cantor0 cardinalidad de 1 cardinalidad de

E() conjunto de las palabras infinitas(V, E, i, t, r) grafo de Mauldin-Williams

R(A) radio espectral deA

dim(F) dimensin fractal


6/94

Contenido

Prefacio iii

1 Autosemejanza 1

1.1 Sistemas iterados de funciones 1

1.2 Mtrica Hausdorff 2

1.3 Atractores para sistemas iterados de funciones 5

1.4 Espacios de hileras 16

1.5 Grafos 19

2 Sistemas de numeracin 26

2.1 Bases para nmeros reales 26

2.2 Bases para nmeros complejos 27

2.3 Representacin de los enteros Gaussianos 28

2.4 Ejemplos de conjuntos de fracciones 30

3 Dimensin Hausdorff 33

3.1 Dimensin topolgica 33

3.2 Generacin de medidas 34

3.3 Medida Hausdorff 36

3.4 Dimensin de semejanza vs dimensin Hausdorff 39

3.5 Dimensin Hausdorff vs dimensin del grafo 42

3.6 Otras dimensiones fractales 47

4 Aplicaciones 50

4.1 Los dilemas espaciales de evolucin 50

4.1.1 Dilema del Prisionero 51

4.1.2 La invasin de delatores: Un caleidoscopio evolutivo. 56

4.1.3 Un fractal dinmico 57

4.1.4 Conclusiones 59

4.2 Compresin de imgenes 60

4.2.1 Comprimiendo imgenes con IFSs 61

4.2.2 Descomprimiendo imgenes con IFSs. 62

4.2.3 Mtodos de particin de imgenes 65


4.3 Crecimiento Fractal y el modelo D.L.A. 67

4.3.1 Procesos de crecimiento fractal. 68

4.3.2 Simulaciones de algunos procesos de crecimiento. 70

4.3.3 Estimando la dimensin fractal. 72

v


7/94

1


Apndice A: Programas 75

A.1 Mathematica 75

A.2 Logo 79

A.3 DraTEX 81

Bibliografa 83

Bibliografa 83

Indice Analtico 85

Sobre los autores 87


8/94

1 AUTOSEMEJANZAEn esta seccin se introduce el concepto de autosemejanza de un conjunto, que se formaliza usandosistemas iterados de funciones, se define el atractor para un sistema y su dimensin de semejanza.Se presentan algunos conjuntos clsicos, se muestra que cada uno de ellos es el atractor para unsistema iterado de funciones y algunas propiedades de estos conjuntos que van a ser de utilidad alo largo de este trabajo. Se identifica E(), el espacio de hileras infinitas, con algn atractor de unsistema iterado de funciones en

n.

1.1 Sistemas iterados de funciones

Una de las formas ms populares para generar fractales es utilizar el concepto de los sistemas

iterados de funciones, que introdujo Michael Barnsley en el ao de 1985, dado que estos conjun-tos presentan autosemejanza, es decir, el conjunto se puede descomponer en un nmero finito departes de modo que una de ellas es idntica, salvo escala, al todo. Para definir formalmente autose-mejanza de conjuntos, se darn algunas definiciones bsicas.

Una funcin f: S T con (S,)y (T, )espacios mtricos, cumplecon lacondicin de Hlder de exponentesi existe una constante

c > 0tal que para x, yS se cumple

(f(x), f(y)) c(x,y) (1.1)

Si = 1se dice de Lipschitz, o de crecimiento acotado. Si cumple

con

(f(x), f(y)) c(x,y) (1.2)

se llama dedecrecimiento acotado. Cuando cumple con ser de crec-

imiento acotado y de decrecimiento acotado se llama distorsin aco-

tada.


9/94

Una funcin f: S T con (S,)y (T, )espacios mtricos, es unasemejanza de razn r, con r > 0, si cumple

(f(x), f(y)) =r(x,y) x,yS. (1.3)

tambin se le conoce comoaplicacin afnde razn r.

Es claro que cuando una funcin cumple con la condicin de Hlder con > 0, es continua,adems cuando es una distorsin acotada es un homeomorfismo. La continuidad no se aseguracuando solo es de decrecimiento acotado. Toda semejanza es una distorsin acotada. Se puedendescribir las semejanzas de 2 en 2 como traslaciones, rotaciones, reflexiones o composicionesde estos tres tipos de transformaciones.

Una lista finita de razones es una n-tupla ordenada (r1, r2, . . . , rn)de nmeros positivos; la lista se llama contractiva cuando ri < 1,i = 1 , . . . , n. Un sistema iterado de funciones en un espaciomtrico S que realiza una lista de razones, es una lista (f1, f2, . . . ,fn)de semejanzas de razn ri res-pectivamente. Un conjunto compacto no

vaco K S es un conjunto invariantedel sistema iterado de fun-ciones(f1, f2, . . . ,fn)si y solo si

K=n

i=1

fi[K].

en este caso se dice que K es autosemejante.

Teorema1. Sea(r1, r2, , rn)una lista contractiva de razones. Entonces existe un nico nmero no neg-ativo s que satisface ni=1 r

si =1. El nmero s es0si y solo si n =1.

Demostracin. Sea n 1 y defina (x) = ni=1rxi, esta funcin es continua, derivable y ddx =

ni=1r

xi ln(ri); esta derivada es negativa por lo que(x)es estrictamente decreciente y como(0) =

ny limx (x) =0, por continuidad existe uns > 0 tal que(s) =1.

La dimensin asociada a (r1, r2, . . . , rn), una lista contractiva de ra-zones, es el nmero positivo s tal que

rs1+rs2+ +rsn =1

y se denominadimensin de semejanza.

1.2 Mtrica Hausdorff

Felix Hausdorff describe la convergencia de conjuntos definiendo una distancia entre los mismosque no requiere encontrar parametrizaciones de ellos, lo cual para nuestros propsitos es conve-niente, ya que se desea analizar la convergencia de sucesiones de compactos en un espacio mtricocompleto. AquLdenota la medida en el sentido de Lebesgue en yLd la correspondiente para

d.

2


10/94

3

Sean A, B S acotados, de un espacio mtrico (S,)y sea r >0. Sedefine un r-vecindarioocuerpor-paralelode A por

Nr(A) ={yS : (x,y) r para algn xA}

Se define la funcin sobre subconjuntos acotados de S, D(A, B)como:

D(A, B) = inf

{r: A

Nr(B)y B

Nr(A)

}

Esta funcin no define una mtrica para los subconjuntos acotados de S, pero si se restringe alconjunto de los subconjuntos compactos de S no vacos,K(S), s lo es. En este casoD se llama lamtrica Hausdorff.

Teorema2. Sea S un espacio mtrico, entonces D(A, B) es una mtrica sobre K(S). Adems si S es completoK(S)es tambin completo.Demostracin. Vase [9,p. 66-67].

Ahora recordemos el teorema de la aplicacin contractiva. Este dice que si f: S Ses una apli-cacin contractiva ySes un espacio mtrico completo existe un nico punto fijo de f,xSque sepuede encontrar a partir de la sucesin:

x0 = aS (1.4)xn = f(xn1), n1. (1.5)

Esto ser especialmente til para el siguiente teorema.

Teorema3. Sea(S,)un espacio mtrico completo, sea(r1, r2, , rn)una lista de razones contractiva, ysea(f1, f2, , fn)un sistema iterado de funciones en S que realiza esta lista de razones. Entonces existeun nico conjunto compacto no vaco, invariante para el sistema iterado de funciones.

Demostracin. SeaF :

K(S)

K(S)definida por

F(A) =n

i=1

fi[A]

Entonces como A es compacto, fi[A]tambin lo es. As F(A)es la unin finita de compactos, quees compacta. Definar = mn{r1, r2, . . . , rn}, claramente 0 < r < 1, para usar el teorema del puntofijo necesitamos demostrar que F es contractiva. Sea B K(S)y seaq > D(A, B)arbitrario y seax F(A). Entonces para algn i tenemos x = fi(a)con a A; existe b Btal que (a, b) < qpuesq > D(A, B)entonces(fi(a), fi(b)) =r i(a, b) < rqde donde F(A) Nrq(F(B)). De formasimilar se obtiene F(B) Nrq(F(A)), y D(F(A), F(B)) < rqentoncesD(F(A), F(B)) < rD(A, B)as Fes contractiva y utilizando el teorema del punto fijo existe un nico conjunto compacto novaco invariante.

La unicidad del punto fijo hace que no importe el conjunto de K(S)que se elija para construir unasucesin, el lmite es siempre el mismo.

Corolario1. En la notacin del teorema anterior, si A 0 es cualquier conjunto compacto no vaco en S, y siAk+1 =

ni=1 fi[Ak], para k0, entonces la sucesin(Ak)converge en la mtrica Hausdorff al conjunto

invariante del sistema iterado de funciones.


11/94

4 AUTOSEMEJANZA

El conjunto invariante de un sistema iterado de funciones contractivo

es llamado el atractordel sistema. En este caso se define la dimensin

de semejanza del atractor como la dimensin s asociada a la lista de

razones.

Esta dimensin para el atractor es dependiente del sistema de funciones, por ejemplo, dado elintervalo[0, 1]y dos semejanzas de razn 12 que apliquen[0, 1]a los intervalos

0,12 y

12 , 1

re-spectivamente, es claro que la dimensin de semejanza es 1. Ahora considere otras semejanzas derazn 34que apliquen[0, 1]a los intervalos

0,34

y

14 , 1. Al calcular la dimensin de semejanza se

obtiene un nmero mayor que 1, es ms, si se toman dos semejanzas de razn nn+1 que apliquen[0, 1]a los intervalos

0, nn+1

y 1

n+1 , 1se observa que la dimensin de semejanza aumenta con-

formen crece, esto se debe a que el traslape es muy grande. En el teorema5se da una condicinsobre las intersecciones de las imgenes para evitar esta situacin. Algo similar se hace en3.4.

Proposicin1. Sea S un espacio mtrico completo, (r1, r2, , rn)una lista contractiva de razones, y sea(f1, f2, , fn)un sistema iterado de funciones sobre S que realizan esta lista de razones. Para la sucesin(xm)definida por: x0= a, xm= fkj (xm1)con kj {1 , 2 , . . . , n}para m 1, se tiene que

1. Todo punto de acumulacin de la sucesin(xm)pertenece al atractor K del sistema.

2. Todo punto de K es un punto lmite para alguna sucesin de(xm)en S.

Demostracin. Defina A0 ={a}y Ak+1 =ni=1 fi[Ak]esta sucesin converge por el corolario1alatractorKdel sistema y cumple quexmAmpara cualquier sucesin que se elija. Para probar (1),dado >0 y sea y un punto de acumulacin de la sucesin (xm). Entonces existe N tal queD(Am, K)


12/94

5

y por el teorema4se tiene

Ld(A) =n

j=1

rdj Ld(A) =Ld(A)n

j=1

rdj

y comoLd(A)es finito y diferente de cero, se obtiene 1 = nj=1rdj es decir, la dimensin de seme-janzasesd.

El teorema anterior muestra que si las imgenes de cada par de semejanzas no se traslapan mu-

cho", y si la medida del atractor del sistema iterado de funciones es positiva, entonces el interiordel atractor es no vaco. Esto ser particularmente til para indicar cuando un atractor llena a

d".

1.3 Atractores para sistemas iterados de funciones

En esta seccin se discute sobre tres conjuntos que son clsicos dentro del estudio de los frac-tales. En primer lugar, el Conjunto de Cantor, que present Georg Cantor en 1883, despert granpolmica a finales del siglo pasado. Es un subconjunto de

que tiene propiedades analticas ytopolgicas no intuitivas, poco usuales en subconjuntos de nmeros reales, por lo que es usado

en el anlisis para construir contraejemplos. En segundo lugar, el tringulo de Sierpinski, descritopor Wacaw Sierpinski en 1915, cuya construccin es similar al conjunto de Cantor y como ste, esun fractal. Por ltimo, se presenta una construccin del dragn Heighway descubierto por John E.Heighway en 1967. Es una curva que llena el plano y cuya frontera es un fractal. Todos se puedenver como atractores para sistemas iterados de funciones.

Los conjuntos de Cantor.. Considere el intervaloC0 = [0, 1]y divdalo en tres partes iguales. Alremover el intervalo abierto que corresponde al tercio central, obtenemos

C1 =

0,

13

23

, 1

El siguiente conjunto C2 lo obtenemos removiendo el tercio central a cada intervalo de C1, de

manera que

C2=

0,

19

29

,13

23

,79

89

, 1

y siguiendo de la misma forma obtenemos una sucesin anidada de conjuntos cerradosC0C1C2 . . . cuyo lmite llamamos conjunto de Cantor conjunto de los tercios centrales omitidos,vase figura1.1,y lo denotamos por C.

C0 .......................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................

C1 ................................................................................................................................................................................................................... ...................................................................................................................................................................................................................

C2 ....................................................................... ....................................................................... ....................................................................... .......................................................................

C3 ........................ ........................ ........................ ........................ ........................ ........................ ........................ ........................

C4 ........ ........ ........ ......... ........ ........ ........ ......... ........ ........ ........ ......... ........ ........ ........ ............

Figura 1.1 C =limk Ck=

k=0Ck.

Proposicin2. La dimensin de semejanza de C esln 2/ln3.


13/94

6 AUTOSEMEJANZA

Demostracin. Se tiene que la construccin anterior, conocida como construccin portremas1, cor-responde a la aplicacin del corolario1 para A0 = C0 = [0, 1]con f0(x) = x3 y f1(x) =

x+23 ,

as, el conjunto de Cantor es el conjunto invariante para el sistema iterado de funciones(f0,f1),que realizan la lista de razones(1/3,1/3). Y resolviendo la ecuacin( 13 )

s + ( 13 )s =1 se obtiene el

resultado.

Note que cadaCkcontiene 2k intervalos cerrados, cada uno de ellos de longitud

13

k, y que en

el primer paso quitamos un subintervalo de longitud 13

, en el segundo paso dos intervalos de

longitud 19 , en general, en elk-simo removemos 2k1 intervalos de longitud

13

k. As, la suma de

las longitudes de los intervalos que eliminamos del intervalo [0, 1]es:

13

+2 132

+ 22 133

+ = 13

1 +

23

+

23

2+

= 1

3

1

1 23

= 1

es decir, al conjunto inicial [0, 1], cuya longitud es 1, le hemos quitado intervalos que tienen lamisma longitud 1.

Quin vive en C?

Vamos a determinar ahora, cules nmeros reales pertenecen a C, es decir vamos a caracterizarlos.En primer lugar, por la forma de construirlo, es claro que los extremos de cada intervalo de Ckpertenecen a C, pues si un nmero es extremo de algn intervalo de Ck, ser extremo de algnintervalo deCnpara cualquiern k, y por lo tanto estar en C. Por ejemplo 0, 19 , 29 , 13 , 23 , 79 , 89 , 1,que son los extremos de los intervalos deC2, estn en C. Para buscar una caracterizacin de todoslos elementos de C, representaremos los nmeros en base 3 (representacin tridica). Recordemosque para cualquierx

, existen

y an, . . . , a0, a1, . . . {0,1,2}, conan=0, tales quex = (an an1. . . a1a0, a1. . . )3

= an 3n + +a1 31 +a0 30 +a1 31 + Ntemos que la representacin tridica para cualquier x [0, 1]es (0, a1a2. . . ak. . . )3, con ai{0,1,2},i . Si a1 = 0 entonces x

0, 13

, si a1 = 1 entonces x

13 ,

23

, y si a1 = 2

entoncesx 23 , 1. Como en el primer paso de la construccin de C removimos 13 ,23, cualquiernmero en C tiene una expresin con a1=1; luego si a1 {0, 2} ya2 =1 entoncesx

19 ,

29

7

9 ,89

, por lo que no estar en C2y por consiguiente tampoco en C, o bien es un extremo de estos

subintervalos y tiene otra representacin cona2=1. As, en el k-simo paso de la construccin deC quedan solamente los nmeros que tengan una representacin con a1= 1,. . . , ak=1, de estaforma obtenemos el siguiente resultado:

Teorema6. Para x[0, 1]: x C si y solo si se puede representar en base3usando solamente0y2comodgitos.

Si se numeran los intervalos de Ckde 1 a 2 k, se puede mostrar que ak=0 si el nmero est en unintervalo impar y 2 si est en uno par.

1Del latntremissis, moneda romana que vala la tercera parte de un slido de oro.


14/94

7

Ejemplo1. Algunos elementos de C son:

(0,02)3= (0,020202...)3= 2 32 +2 34 + = 14(0,022)3= (0,022022022... )3 =

413

(0,0022)3 = (0,002200220022...)3 = 1

10

(0,20022)3 = (0,200222002220022...)3 = 85121

Los elementos que pertenecen al conjunto C, dados en el ejemplo anterior, son todos racionales,sin embargo, algunos elementos de este conjunto son irracionales.

Ejemplo2. Es claro que (0, 202002000200002 . . . )3 es un nmero irracional y adems, pertenece aC.

Teorema7. Si x C, entonces1 x, x3 , x+23 C.

Demostracin. Comox C, seax = (0, a1a2. . . ak. . . )3, conai {0, 2}, i :

1. Como

1 x = 2

i=1

3i

i=1

ai3i

=

i=1

(2 ai)3i

y comoai {0, 2} entonces 2 ai {0, 2}, por lo tanto 1 x C.

2. Comox

3=

13 x = (0, 1)3 (0, a1a2. . . ak. . . )3

= (0, 0 a1a2. . . ak. . . )3

se tiene que x3 C

3. Como

x+23

= (0, 1)3 [(0, a1a2. . . ak. . . )3+ (2)3]= (0, 1)3 (2, a1a2. . . ak. . . )3= (0, 2 a1a2. . . ak. . . )3

se tiene que x+23 C

Ejemplo3. Como sabemos que 14 C, se tiene que 34 C pues 34 =1 14 , adems, 112 C pues1

12 = 1/4

3 .


15/94

8 AUTOSEMEJANZA

Cardinalidad y algunas propiedades de C

Consideremos el conjunto

A={f: {0, 2} / fes funcin}

La cardinalidad de Aes|A| =|{0, 2}|| | =20 =1 =| |, de manera queA es no numerable.Adems, para toda f A, existe un nicox = (0, f(1)f(2)f(3) . . . )tal quex C, es decir, existeuna biyeccin entre A y C, por lo que |C| =1. En otras palabras, C tiene la misma cantidad deelementos que tiene

!. A pesar de esto C posee una estructura topolgica muy diferente:

1. C es compacto:Es cerrado pues es la interseccin numerable de conjuntos cerrados, y C esacotado, por el teorema de Heine-Borel, es compacto.

2. C no contiene ningn intervalo:Suponga que I =]a, b[ C, entonces I Ckk . ComoCkesta formado por 2 k intervalos cerrados disjuntos, Ies subconjunto de algn intervalo de

tamao

13

k, por lo queb a

13

k k , lo que implicara queb = a.3. C no tiene puntos aislados:Sixno es extremo de ningn intervalo deCkpara algnk, seaxnel

extremo izquierdo del intervalo deCnque contiene ax; luego 0 < x xn 13

n, por lo que

xn x. Si x es extremo izquierdo en algn intervalo de Ckpara algn k, tome x ncomo elextremo derecho de ese intervalo parankyxn = 1 en otro caso; por un argumento similar,xnx .

En suma C es un conjunto totalmente disconexo, compacto y perfecto. Adems es no numerabley tiene medida cero. En general un conjunto de Cantor es un conjunto que cumple con estas tresprimeras propiedades, y se puede demostrar que todos los conjuntos de Cantor son homeomorfos.Sean f1(x) = x3y f2(x) =

x+23 con dominio y codominio igual aC; ambas funciones son inyectivas

y:

f11

C

0,13

= f12

C

23

, 1

= C

Esto significa que si observamos solamente la mitad derecha o la mitad izquierda del conjunto de

Cantor obtenemos una copia homeomorfa de este. De manera que podemos encontrar una copiahomeomorfa del conjunto de Cantor incluida en la interseccin de C con cualquier intervalo deCk(tan pequeo como queramos tomandoksuficientemente grande).

Generalizacin de C

La construccin de C se puede generalizar de manera evidente, quitando un subintervalo abiertocentrado de longitud , con ]0, 1[, y seguir con un proceso anlogo al del caso = 13 . Porejemplo, para = 15 se tiene C0 = [0, 1], C1 =

0,25 35 , 1, C2 = 0, 425 625 , 25 35 ,1925

2125 , 1. Al conjunto lmite de esta sucesin lo denotamos 1

5, en general a conjuntos generados as

los denotamos por . Note que C = 13.

Notemos que el tamao de C1es 1 y est compuesto de dos intervalos cada uno de longitud1

2 =: ; as cada Ckest compuesto por 2k intervalos de longitud k y los intervalos que re-

movemos en elksimo paso miden k1. Por ejemplo con = 25tenemos 15 y 35 se obtiene con= 15 .Para cualquier]0, 1[yxen , definimos ladireccindexen como la sucecin {s0, s1, s2, . . . },donde cadasies 0 1. Para saber qu valor asignamos a snbasta con enumerar los intervalos de


16/94

9

Ckde 1 hasta 2 k,sk1ser 0 si x est en un intervalo impar y 1 si est en uno par. As definida ladireccin dexen , es fcil ver que este tiene representacin nica de la forma:

x=

i=0

sii(1 )

As como caracterizamos los elementos de C como los nmeros que se pueden representar en base3 usando solamente 0 y 2 como dgitos, podemos caracterizar algunos de la siguiente manera:

Teorema8. Si n

, n3y = 1n entonces

={(0, a1a2. . . ak. . . )n / ak {0, n 1}}

Ejemplo4. Conn =4 obtenemos

12

={(0, a1a2. . . ak. . . )4 / ak {0, 3}}

As 45 = (0,30)4 12 . Otros elementos de 12 son: 116 ,

120 ,

6364 y

15 . Aplicando reiteradamente las

funciones: g1(x) = 1 x, g2(x) = x+34 y g3(x) = x4 , a elementos de 12 , obtenemos otros de suselementos.

Ejemplo5. Conn =5 obtenemos 35, y algunos de sus elementos son: 16 , 56 , 2930y 2531 .

Se pueden construir conjuntos de Cantor dividiendo a [0, 1]en n partes iguales y dejar algunossubintervalos de longitud = 1n(no necesariamente los intervalos laterales como en C).

Teorema9. Sea n

, n 3, D ={0 , . . . , n 1} y B subconjunto propio de D con |B| 2, entonces

nB ={(0, a1a2. . . ak. . . )n / akB}

es un conjunto de Cantor.

En la figura1.2,conn =5 y B={1,2,4}, se muestra 5{1,2,4}. Se debe notar que este conjunto estformado por los nmeros en [0, 1]que en base 5 tienen representacin utilizando solamente a 1, 2y 4 como posibles dgitos.

C0 .............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................

C1 ......................................................................................................................................................................................................................................................................................... .............................................................................................................................................

C2 ................................................................................................................. ......................................................... ......................................................... .............................

C3 ............................................. ....................... ....................... ............ ....................... ............ ..................

C4 .................. ......... .............. .............. ........ .............. ........ ........ ........

Figura 1.2 5{1,2,4} = limk Ck.

En general a partir de un elemento xde nBse pueden obtener ms elementos aplicando reiterada-mente las funciones: fi(x) =

x+ain , conai B.

Relacin de C con el espacio de arreglos

Denotamos porE() el espacio de losarreglos infinitos de0y1. Seag : E() , que interpreta unarreglo como un nmero en base 2, cuya parte decimal es el arreglo y la parte entera es cero.


17/94

10 AUTOSEMEJANZA

Ejemplo6. g(001) = (0,001)2 = 17 .

Como todo nmero real tiene expansin en base 2, tenemos queg(E()) = [0, 1], y si definimosf: E() de la misma forma queg, pero cambiando los dgitos 1 por 2 y la representacin enbase 3, tenemos que f(E()) = C. Es claro que fas definida es un homeomorfismo entre E() yC.

Ejemplo7. f(001) = (0,002)3= 113 C.

Un resultado muy interesante es el hecho que un conjunto cero dimensional y separable es deCantor si es homeomorfo a un subconjunto de E(), vase [9].

Sobre el tamao de

En este momento es oportuno preguntarnos ser 15

ms grande que 35?. El siguiente grfico

indica que la sucesin de Ckque converge a 35

se desvanece ms rpido que la sucesin queconverge a 1

5, por lo que en algn sentido 3

5ser ms pequeo" que 1

5.

...........................................................................................................................................................................................................................................................

................................................... ...................................................

........... ........... ........... ...........

... .. ..... ... .. .. ...

...........................................................................................................................................................................................................................................................

..................................................................................................... .....................................................................................................

......................................... ......................................... ......................................... .........................................

................. ................. ................. ................. ................. ................. ................. .................

Figura 1.3 Comparacin de 35

y 15

.

El anlisis sobre el tamao no es evidente ya que ambos conjuntos tienen la misma cardinalidad,adems son conjuntos de medida cero. Para poder hacer alguna diferencia entre estos definimos elconjunto:

={x y / x,y }={t / (+t)= }con + t ={x+t / x }, que es una traslacin de en [t, 1+t], y as se puedeinterpretar como los tiempos donde una copia de interseca a recorriendo el ejexcon veloci-dad constante. Con este conjunto podemos diferenciar 1

5de 3

5en el siguiente sentido: cuanto

mayor sea , significa que se intersecar durante ms tiempo con una copia suya, por lo

que en este sentido ser un conjuntoms grande. Por ejemplo, en [25] se prueba que 35 3

5es

un conjunto de Cantor de medida cero, y es fcil ver que 15 1

5= [1, 1], por lo que 1

5es ms

grande que 35. El valor = 13es lmite para comparar conjuntos de esta naturaleza [25], en este se

prueba que si > 13 , L( ) =2 y si < 13 , L( ) =0.Recordemos que en la construccin de C removimos el tercio central a cada intervalo. Sea C

=

3{0,1}, cuya construccin es anloga a la de C pero quitando en cada paso el intervalo semiabierto,cerrado a la derecha, correspondiente al tercer tercio de cada intervalo. El lector puede verificar que

C C = [1, 1]mientras que CC = 12 ,12

, de donde se concluye que C es ms grande

que C.

Notemos que para algunost

[

1, 1]se tiene que

(+t)

= . Cuntos elementos tiene

(+t)dependiendo de la escogencia det?. Un resultado muy interesante es el siguiente:Teorema10. Si 1) (1.6)

en el primer caso se tiene quea1 b1 = 0; en el segundo casox = 12y y = 12y en este caso se puedecambiar la representacin dexo deypara quea1 b1 = 0.Denote conS0kel tringulo con vrtice(0, 0)en el pasok-simo, asS00 = S0,S01 ={(x,y): 0x+y 12} en generalS0k={(x,y): 0 x +y 12k}, ntese que

(x,y) = ((0.00 ak+1ak+2 )2, (0.00 bk+1bk+2 )2)S0k ak+1 bk+1 = 0.

Adems, cualquier tringulo de Skes de la forma(u, v) +S0kdonde(u, v)es un vrtice izquierdode algn tringulo de Sk. As, dada una combinacin de a1, . . . , an, b1, . . . , bn {0, 1}tal que si


20/94

13

ai=1 entoncesbi = 0, la expresin

(0, 0) +a12

(1, 0) +b12

(0, 1) +a24

(1, 0) +b24

(0, 1) +

+ an2n

(1, 0)+bn2n

(0, 1)

es un vrtice izquierdo de Sngenerado a partir de (0,0) y los pasos 1, 2 . . . n. En base 2 este vrticese escribe

(u, v) = ((0.a1a2 an)2, (0.b1b2 bn)2) . (1.7)Hay 3n de estos puntos enSnpues, al escogera i1 = ai2 = = a ij =1, con j =0, . . . , ny el restocero, se tiene 2nj formas de escoger b1, b2, . . . , bncon a i bi =0 y como hay(nj )formas de elegirlos a ik=1, k=1, . . . , jen total se tienen(

nj ) 2nj formas de escogerlos. Variando j =0, . . . , nse

obtiene

2n +

n

1

2n1 +

n

2

2n2 + + 1= (2+ 1)n =3n (1.8)

formas diferentes de escoger los ai, i = 1, . . . , nybi, i=1, . . . , ncona i bi =0. Por lo tanto todoslos vrtices izquierdos deSnson de la forma(1.7). Algunos vrtices de la forma (1.7) son:

34

,18

= ((0.110)2, (0.001)2)

1116

, 132

= ((0.10110)2, (0.00001)2)

Esto permite dar una descripcin de los elementos de S, que se resume en el siguiente teorema.

Teorema11. Sea S0un tringulo equiltero de lado1. Introduzca un sistema de coordenadas con origen enun vrtice de S0 y los lados adyacentes en la parte positiva de cada eje. Entonces, (x,y) S si y solo silasexpansiones binarias de ambas coordenadas se pueden escribir sin que tengan un1en la misma posicin.

Demostracin. Seas = ((0.a1a2

)2, (0.b1b2

)2)con a i, bi

{0, 1

}, i

. Seas

Sy n

fijo, comosSns = (u, v) + (x,y)

con (u, v)un vrtice izquierdo de la forma(1.7)y (x,y) S0n entonces an+1 bn+1 = 0. Porotro lado si, s = ((0.a1a2 )2, (0.b1b2 )2)no tiene un 1 en la misma posicin, sea nnaturalfijo, entonces se tiene que ((0.a1a2 an)2, (0.b1b2 bn)2)es un vrtice izquierdo de Sn y x =(0.00 an+1 )2 y y = (0.00 bn+1 )2 cumplen con (x,y) S0n pues an+1 bn+1 = 0entoncessSnn por lo tantosS.

Algunos elementos deSson

272341

, 68341 = (0.11001100002, (0.0011001100)2)

79

,1063

=

(0.110001

2, (0.001010)2)

Se puede observar de la construccin por tremas deS, que ste es semejante a su parte superior,o a la parte derecha o a la parte izquierda, independiente de la escala, pues no importa cunto seaumente una parte adecuada de la figura, siempre se observa el mismo detalle, la razn de esto esqueSse puede construir por medio de un sistema iterado de funciones .


21/94

14 AUTOSEMEJANZA

Sean f0, f1, f2 : 2 2 tal que f0((x,y)) = 12 (x,y), f1((x,y)) = 12 (x,y) + 12 (1, 0)y f2((x,y)) =12 (x,y) +

12 (0, 1). Rtese el eje Yun ngulo de 30

o a favor de las manecillas del reloj, note queestas funciones son semejanzas de razn 12 . Con esto se define un sistema iterado de funcionesque realizan la lista contractiva de razones ( 12 ,

12 ,

12 ). El atractor del sistema iterado de funciones

(f0, f1,f2)esS. Esto dice tambin que la dimensin de semejanza de S =ln(3)/ ln(2).

Una sucesin que aproxima a un conjunto.. En las construcciones anteriores se necesita de unconjunto, y a partir de ste se construye por un mtodo iterativo a S. Es posible sin embargo,

ocupar en la computadora mucha memoria para hacer tales iteraciones sobre todos o una granparte de los elementos de un conjunto, ya sea un tringulo o cualquier otro compacto. An as, elcorolario1afirma que cualquier compacto no vaco sirve como primera aproximacin para S, demanera que si se utiliza un punto y sobre l se evala iteradamente las funciones f0, f1,f2en unorden aleatorio eventualmente se tendr una aproximacin de S.Cul ser un buen punto de partida y un buen orden de iteracin para asegurar que por igual seest aproximando a todos los puntos deS? Defina Akal conjunto formado por todos los vrticesizquierdos de cada tringulo en Sk. Akes una aproximacin de todos los puntos de Sky tambina los elementos de S , adems, la distancia de algn elemento de Aka otro de S es a lo sumo

12k

por lo que es clara la convergencia. Basta entonces definir una sucesin en que todos los vrticesizquierdos deSkformen parte de ella.

Observe que, como todos los vrtices izquierdos de Skson de la forma(1.7)se les puede codificarcon la expresin ckck1 c1de la siguiente forma: c i = 0 si a i = 0 y b i = 0, c i = 1 si a i = 1 ybi =0 yc i =2 si a i =0 ybi =1, y como a ckck1 c1se le asocia un nico nmero entero n talquen = (ckck1 c1)3, as se tiene una forma de asociar todos los vrtices izquierdos de Skconun nico nmero entero, por ejemplo

1116

, 132

= ((0.10110)2, (0.00001)2)(21101)3=199,

38

,1732

= ((0.011000)2, (0.100010)2)(020112)3=176,

sta es la sucesin que se define en el siguiente teorema.

Proposicin3. Sea f0, f1, f2las funciones definidas en la construccin anterior. Sea n = (ckck1. . . c2c1)3la expansin tridica para el nmero entero no negativo n, defina x n = (fc1 fc2 . . .fck1 fck)((0, 0)),

y sea Akel conjunto formado por los vrtices izquierdos de cada tringulo que forma S k. Entonces Ak ={x0, x1, x2, . . . , x3k1}.Demostracin. Sea k

y 0 n < 3k, n = (ckck1. . . c2c1)3 y sea (u, v) 2 tal que u =0.a1a2 aky v = 0.b1b2 bk con ai = ci(2 ci) y bi = ci2(ci 1) para todo i = 1, . . . , k, esclaro que (u, v) Sk, adems que fc1 ((0.a2 ak)2, (0.b2 bk)2) = (u, v), en consecuencia(fc1fc2 )((0.a3 ak)2, (0.b3 bk)2) = (u, v)y en general

xn = (fc1fc2 . . .fck1 fck)((0, 0)) = (u, v)entoncesxn

Aky como

|{xn: 0

n < 3k

}|=3k por lo que Ak=

{x0, x1, . . . , x3k

1

}.

Corolario2. S={xn}0 .Demostracin. Basta notar que Ak+1 = f0[Ak]

f1[Ak]

f2[Ak]y usando el corolario1se obtiene

la convergencia.

En la Figura1.5, se observan algunas aproximaciones de S, usando la sucesin anterior con k= 1,2, 3, 5, 6 y 7.


22/94

15

Figura 1.5 Vrtices deSk

Teorema12. El atractor del sistema iterado de funciones (f0, f1,f2)es el tringulo de Sierpinski S.

Luego la dimensin de semejanza de S = ln(3)ln(2)es igual a la dimensin fractal que sucede cuandofi[S0]no traslapan demasiado.

Corolario3. Sea A0

2 compacto y no vaco, defina

An+1= f0[An]

f1[An]

f2[An]

entonces esta sucesin converge a S en la mtrica Hausdorff del espacio de los compactos no vacos de 2.

Dragn de Heighway.. Este conjunto se define como el lmite Hde la sucesin de polgonos Hndada por la Figura1.6. Este fue descubierto por el fsico John E. Heighway que junto con Bruce A.Banks y William Harter estudiaron algunas propiedades de los polgonos aproximantes, entre ellasel hecho de que stos nunca se cruzan [9,p. 21].

Q

P

.

..

.

.

.

..

.............

.

..

.

..

..

.

..

.

.

.

.

.

.

.

.

..

.

..

.

.

.

.

.

.

.

.

..

.

..

..

.

..

.

.

.

.

.

.

..

..

.

..

.

.

.

.

.

.

.

.

..

.

..

.

..

..

.

.

.

.

.

.

.

Q

P

.

............................

..

...............................................................................................................

........................................................................

.

..

.

..

..

.

..

.

.

.

.

.

.

.

.

..

.

..

.

.

.

.

.

.......................................................................................................

.......

........

...................

...................................................................

...........................................................................................................................................................................................

.

..

.

.

.

..

..

.

..

.

.

.

..

.

..

..

.

.................................................................................

..

.

.

.

..

.............

.

..

.

..........................................................................................................

.

..

..

.

.

.

.

.

.

..

.

..

..

.

..

.

.

.........................................................................................................

.

.

.

.

.

.

.

.

..

.

..

.

..

..

.

.

.

.

.

.

...........................

Figura 1.6 Construccin del Dragn de Heighway.

Proposicin4. Existen dos semejanzas f1, f2 : 2 2 con razn 12 tal que H es el atractor de estesistema iterado.

Demostracin. SeanPyQlos puntos de la Figura1.6. ConsiderePcomo el origen de coordenadas,as, el puntoQ = (q1, q2)tiene coordenadas(0,1/2)en el caso H0y (1/2,1/2)en el casoHkparak1. Se necesita que Hk+1 = f1[Hk]f2[Hk]. Se va a describir el efecto sobreHk, de cada una delas funciones. f1primero trasladaHkde modo que el puntoQcoincida con el origen, luego contrae

por un factor de 1/2 y por ltimo rota un ngulo de 135o; anlogamente se describe f2con ladiferencia de que la rotacin es con un ngulo de 45o. As, para un punto(x,y) Hkse obtiene

f1(x,y) = 1

2(x q1,y q2)

cos135o sen135o

sen135o cos135o

f2(x,y) = 1

2(x q1,y q2)

cos45o sen45o

sen45o cos45o


23/94

16 AUTOSEMEJANZA

simplificando parak 1, f1(x,y) = 12 (1 x y, x y)y f2(x,y) = 12 (x y, x+y 1), que sonsemejanzas de razn 1

2y describen la construccin anterior.

Figura 1.7 Dragn de Heighway.

Con esta lista de razones se calcula la dimensin de semejanza de Hla cual es 2.

1.4 Espacios de hileras

Considere un alfabetoE ={1 , 2 , . . . , n} denletras, y el conjunto E(m) de todas laspalabrasohilerasfinitas usandomletras de E. Se denota porE() el conjunto formado por todas las palabras finitasy porE(), el conjunto de las infinitas.La hilera de longitud cero es la palabra vaca y se denota por . La hilera finita representa unancestro desi y solo sies un segmento inicial deesto es = para alguna hilera, se dicetambin que es un prefijo de ; la longitud de se denota||. SobreE() se define una relacinde orden parcial " tal que sies un prefijo comn de . As paraE() se define por:

[] =

E()

: ,el conjunto de todos las hileras infinitas que empiezan con , y satisfacen[] = [1] [2] [n]y = [1] [2] [n].SobreE() E() se definerporr(, ) =rk dondekes el largo del mayor prefijo comn dey. Esta funcin define una mtrica enE() cuando 0 < r < 1 como se ver en el siguiente teorema.

Teorema13. Sea(E(),r)definida anteriormente. Entonces, se cumple

(1) res una ultramtrica2 sobre E().

(2) Los conjuntos[]tienen dimetro r||.

(3) El espacio(E(),r)es completo.

Demostracin. Para (1) se probarr(, ) mx{(, ),(, )}nicamente pues las otras condi-ciones son claramente satisfechas. Seak1la longitud del mayor prefijo comn ay,k2la longituddel mayor prefijo comn a y, ykla longitud del mayor prefijo comn a y. Ahora considerem = mn{k1, k2}, se cumple que k my por lo tanto r(, ) = rk rm = mx{rk1 , rk2} =

2Una ultramtrica es una mtrica que cumple (x,y) mx{(x,z),(z,y)}, x,y,z.


24/94

17

mx{r(, ),r(, )}, como se deseaba. Para la parte (2) escoja= y = dondees sumayor prefijo comn, se tiene que , []y por lo tanto diam []r(, ) =r ||. Para obtenerla otra desigualdad, sean, []cualesquiera, y sea el mayor prefijo comn entre ellos, secumple que|| ||as que r(, ) = r|| r||y por lo tanto diam [] r||. Para la ltimaparte, dada(p)sucesin de Cauchy en E(), para cadak existe unpk de modo que paratodo p, m pkse tiene que r(p, m) < rk, es decir, pkcoincide con men las primeraskletraspara todomk, es por esto que se define , donde suk-sima letra sea la k-sima depk. Resultaquep

, pues dado > 0, se puede encontrark

tal querk < , y entonces para todom > p kse tiene quer(m, ) rk < . Con lo que se finaliza la demostracin de este teorema. Se puede dotar aE() de otra mtrica a partir de una familia de pesosw > 0, E() que satisfacew > wsi < siempre y cuando para toda E() la sucesin de pesos al recorrer la hilera tienda a cero. Esta tambin cumplir que diam [] =w.

Proposicin5. Si (, ) = w, donde es el mayor prefijo comn entre , y (, ) = 0si = entoncesdefine una ultramtrica sobre E().

Demostracin. Vase [9,p. 71].

Sea (r1, r2, , rn) una lista de razones contractiva, E ={1,2, , n}el alfabeto de n letras y E

()

el espacio de las hileras in-finitas sobre E. La lista de razones(r1, , rn)se denota por(re)eE.Para cada e E, existe una funcin e : E() E(), que se llamacorrimiento a la derecha, definida pore() =e.

Proposicin6. Sea E(),(re)eEuna lista de razones contractiva y sean wdefinidos recursivamentepor: w =1, we =re w. Entonces existe una ultramtricaen E() tal que(, ) =w, donde esel mayor prefijo comn deyy se cumple que eldiam [] =w.

Demostracin. Es inmediata de la proposicin5pues la lista de razones define una familia con lascondiciones de esta proposicin.

A la mtrica definida en la proposicin6se le llama la mtrica inducida por la lista de razones(re)eE. Con esta mtrica los corrimientos a la derecha forman un sistema iterado de funciones,esto se formaliza en la siguiente proposicin.

Proposicin7. Sea la lista contractiva de razones (re)eE y (e)eE los corrimientos a la derecha y sea(E(),)el espacio de hileras infinitas de n letras con la mtrica inducida por la lista de razones. Entonces(E(),)es un espacio compacto y separable.

Demostracin. Con una demostracin similar a la del teorema13,el espacio(E(),)es completo,adems, se puede ver que el sistema iterado de funciones(e)eErealiza la lista de razones(re)eE,dado que si es el mayor prefijo comn entre y se tiene queees el mayor prefijo comn deeye, de donde (e() , e()) =we= rew=re(, ). Esto significa queees una semejanza

en E(), con raznre. Se verifica que E() es el conjunto invariante de este sistema iterado defunciones, y usando el teorema 3 se prueba la compacidad. Para ver que es separable basta recordarque todo espacio compacto es separable.

El espacioE() se puede identificar con algn atractor de un sistema iterado de funciones en

n.El siguiente teorema define una aplicacin h : E()

n cuyo rango es este atractor. A esta apli-cacin se le llama la aplicacin modelo". Este teorema es un caso particular del teorema41,quedemostraremos en el captulo3.


25/94

18 AUTOSEMEJANZA

Teorema14. (Aplicacin Modelo del Espacio de Hileras). Sea S un espacio mtrico completo no vaco, ysea(fe)eEun sistema iterado de funciones que realiza la lista contractiva de razones(re)eEen S. Entoncesexiste una nica funcin continua h : E() S tal que h(e) = fe(h())para todoE () y para todoeE. El rango h[E()]es el conjunto invariante del sistema iterado de funciones (fe)eE.Proposicin8. La aplicacin modelo tiene crecimiento acotado.

Demostracin. SeaB = diam

h[E()]

.Bes finito y positivo puesh[E()]es compacto. Seany

enE()

yk=|| donde = e1 ekes el mayor prefijo comn de y, es decir= y= entonces (h() , h()) =re1 rek (h() , h())w B= B (, ). Si E ={0, 1}y f0 : y f1 : tales que f0(x) = x3 y f1(x) = x+23 . La aplicacinmodeloh : E()

, descrita en el teorema14,es h(0) = h()3 yh(1) = h()+2

3 y cumple conh[E()] = C.

Proposicin9. h : (E(),r) tiene distorsin acotada si y solo si r= 13 . En estecaso h : (E(),1/3)C es un homeomorfismo.

Demostracin. Suponga quehtiene distorsin acotada, as existen aybtales que:

ar(, ) |h() h()| br (, ), (1.9)adems se tiene:

|h(1) h(1)| = h() + 23 h() +23

=|h() h()|3 (1.10)r(1, 1) = rr (, ) (1.11)

en forma similar

|h(0) h(0)| = 13|h() h()|

r(0, 0) = rr (, )

Si

|

|= n, se puede multiplicar la desigualdad (1.9)por 13n , y usando las ecuaciones(1.10)y (1.11)

se obtiene:a

3nrnr(, ) |h() h()| b3nrnr(, ) (1.12)

Si r > 13 se puede encontrar ntal que b

3nrnr(, ) < ar(, ), con esta desigualdad y la

ecuacin (1.12) se tiene que|h() h()| < ar(, )

quecontradice la hiptesis. Si r < 13se tendra de manera anloga que |h() h()| > br(, )que tambin la contradice, de donde se debe tener r = 13 . En [9,p. 70] se prueba el recproco. Unadistorsin acotada es biyectiva y su inversa es continua, con lo cual se completa la prueba.

SeaE ={L, R, U} y sean fL, fR, fU : 2 2 tales quefL((x,y)) =

12

(x,y)

fR((x,y)) = 1

2(x,y) +

12

(1, 0)

fU((x,y)) = 1

2(x,y) +

12

(0, 1)


26/94

19

Se sabe que estas funciones son semejanzas de razn 12 . Con esto se define un sistema iterado defunciones que realizan la lista contractiva de razones ( 12 ,

12 ,

12 ). Para describir ah, la aplicacin del

teorema14,se usa la expansin en base 2 de las coordenadas del punto (u, v). Si E() y lai-sima letra deesLentonces eli-simo dgito deuyves 0; si esUentonces eli-simo dgito deues 0 y el de v es 1, si es R entonces el i-simo dgito deu es 1 y eli-simo dgito dev es 0. Porejemplo

h(RULRRUL ) =((0.1001100 )2, (0.0100010 )2)

De aqu se tiene que h[E()

] = S. Ademsh cumple con h(L) = fL(h()),h(U) = fU(h())yh(R) = fR(h()), y es continua para todo E().Si se consideraE() con la mtrica 1/2 se tiene que diam [] = (

12 )

||. Se sabe que h tiene crec-imiento acotado, sin embargo no es una distorsin acotada.

Proposicin10. La aplicacin h definida como antes no es de decrecimiento acotado.

Demostracin. Si se toma= (LRRR )y= (RLLL ), se tiene que1/2(, ) = 1 y ademsh() h()

= ((0.0111 )2, (0.0 )2) ((0.1000 )2, (0.0 )2)= 0

1.5 Grafos

Los grafos se utilizan para dar una generalizacin de los espacios de hileras E(). Para hablar degrafos deben existir un conjunto Vde vrtices o nodos y un conjunto E de aristas o flechas. Cadaarista va de un nodo a otro nodo cualquiera. La direccin de la arista en nuestro caso es importantede tomar en cuenta, y por esto se trabajar con grafos dirigidos. Cuando exista ms de una aristaconectando un par de nodos dados se le llamar multigrafo. Es por esto que se darn las siguientesdefiniciones.

Sea V un conjunto finito no vaco y E V V, entonces al par(V, E)se le llama grafo dirigido. Los elementos de V son llamados vrticeso

nodosy los de E sern llamadosaristasoflechas.

Ahora se extiende esta definicin para que pueda existir ms de una arista conectando un mismopar de nodos.

Unmultigrafo dirigido(V, E, i, t), consiste de dos conjuntos finitosV, E, y dos funciones i : EV y t : EV, tales que para cada eE,i(e) es el vrtice inicial de e, y t(e)su vrtice terminal. Denotaremos

Euv al conjunto de aristas e, tales que i(e) =u y t(e) =v. Un camino

en un multigrafo dirigido es una sucesin de aristas, tomadas en ciertoorden de modo que el vrtice terminal de cada arista sea el vrtice inicial

de la siguiente arista. Un multigrafo es fuertemente conectadosi,

para cada par de vrtices u,v de E, existe un camino de u a v.

Un camino ser a menudo identificado con una hilera de etiquetas de las aristas. Adems el vrticeinicial de un camino es el vrtice inicial de la primera arista, anlogamente se define el vrtice final


27/94

20 AUTOSEMEJANZA

de un camino. El nmero de aristas de un camino diremos que es su longitud, la denotamos con||. Un caminoque cumple quei() =t()es llamadociclo, y unlazoes un ciclo de longitud 1.EscribiremosE()uv para denotar el conjunto de caminos con vrtice inicial u y vrtice terminalv osea los caminos que van de uavo que conectanuconv. EscribiremosE(n)uv para todos los caminos

deuavcon longitud n. Diremos para cadauVque el conjunto E(0)uu tiene un elemento, a saberel camino vaco de uen s mismo, escrito u. Por supuesto que vamos a identificar Econ E(1) y a

EuvconE(1)uv. Vamos a considerar E() como el conjunto de todos los caminos finitos en el grafo.

Sea(V, E, i, t)un multigrafo, vamos a considerarE() con una estructura de rbol, es decir, si esun camino entonces los hijos de son los caminos de la forma e, para las aristas eque cumplan quei(e) = t(). Realmente esto no es un rbol sino ms bien una unin disjunta de rboles, un rbol

E()v para cada nodovV. Una unin disjunta de rboles es llamada bosque". As llamaremos a

esto el bosque de caminos del grafo.

Una hilera infinita = (e1e2. . . ) corresponde a un camino infinitosi el vrtice terminal de cada arista coincide con el vrtice inicial de

la prxima arista, es decir, t(en) = i(en+1)n . Dado un grafo(V, E, i, t)escribimos E()para el conjunto de todos los caminos infini-

tos, E()v para el conjunto de todos los caminos infinitos que empiezan

en v, v V. Adems si E(), [] ={ E() : }, elconjunto de todos los caminos infinitos que comienzan con.

Algunas mtricas pueden ser definidas sobre los espacios E()v en forma similar a lo hecho enespacios de hileras en la seccin1.4.Debe tomarse en cuenta la posibilidad de que algunos nodosdeE() no tengan hijos o tengan un nico hijo. As, si no tiene hijos, entonces[] = , y por lotanto su dimetro es 0. Sitiene un nico hijo , entonces[] = [], as se debe cumplir diam [] =diam []. Estos casos no ocurren en grafos (V, E, i, t)donde cada nodo tiene al menos dos aristas

partiendo de este.Sea(V, E, i, t)un multigrafo dirigido. Dada una familia wde nmeros reales positivos, uno paracada camino finitoE (), se definen mtricas; de hecho nicamente se necesita definir distan-cias entre hileras con el mismo vrtice inicial, y as obtenemos espacios mtricos E ()v , disjuntos,uno para cada nodo v V, que llamaremos en adelante espacios de caminos. Mas an, cada define una ultramtrica sobre los espacios E ()v tal que diam [] = wpara la mayora de los ,anlogo a lo hecho en la proposicin5. Pero vamos a estudiar lo anterior, con ms detalle, en laprxima seccin con el fin de definir la dimensin de un grafo.

Autosemejanza de Grafos

Algunos conjuntos no presentan autosemejanza como los vistos en la seccin 1.1,es decir, unaparte no es semejante al todo. Ms bien, el conjunto presenta autosemejanza por pedazos, o sea,este se puede dividir en varias partes que a su vez, cada una de ellas se descompone utilizandolas partes originales afectadas por algn factor de escala. Esto nos permite estudiar una mayorcantidad de conjuntos. Mauldin y Williams en[29] hacen una formulacin de este tema y dan unacorrespondencia entre estos conjuntos y los multigrafos dirigidos. Es por ello que vamos a definira continuacin algunas estructuras nuevas.


28/94

21

La estructura involucrada, un multigrafo dirigido(V, E, i, t)junto conuna funcin r : E ]0,[, ser llamado un grafo de Mauldin-Williams y se denotar por (V, E, i, t, r). Un sistema iterado defuncionesque realiza este grafo est compuesto de espacios mtricos

Sv, uno para cada nodo v, y semejanzas fe, una para cada arista eE,tales que fe : Sv Su si e Euv, cada una con una razn de seme-

janza r(e). Un grafo de Mauldin-Williams (V, E, i, t, r) ser llamado

estrictamente contractivosi r(e) < 1para todo eE.La definicin de la funcinrque evala aristas puede ser extendida a caminos definiendor(u) =1 para caminos vacos, y r(e) = r(e)r()para cualquier camino y cualquier aristaecont(e) =i().La prxima definicin generaliza la definicin1.1, que en este contexto correspondera a un niconodo y un lazo para cada una de las semejanzas.

Una lista invariantepara un sistema iterado de funciones, es una lista

de conjuntos compactos no vacos KvSv, uno para cada nodo vV,tales que

Ku =vV

eEuvfe[Kv] (1.13)

para todo uV. Cada uno de los conjuntos compactos Kvque satisfacetal ecuacin se dir que tiene autosemejanza de grafo.

Teorema15. Dado(V, E, i, t, r)un grafo de Mauldin-Williams estrictamente contractivo y sea (fe)eEunsistema iterado de funciones que realiza este grafo en espacios mtricos completos S v. Entonces existe una

nica lista(Kv)vVde conjuntos compactos(KvSv)tales queKu =

vV

eEuv

fe[Kv]

para todo uV.Demostracin. Sabemos que los espacios mtricos de los subconjuntos compactos no vacos deSv,K(Sv)son completos, por lo tanto el producto cartesiano

vV

K(Sv)

es tambin completo con la mtrica usual del producto cartesiano. Vamos a escribir (Av)vVparaun elemento tpico del espacio producto. La funcin definida por

F((Av)vV)=

vVeEuv

fe[Av]

vV

es una aplicacin contractiva, y su nico punto fijo es

Ku =vV

eEuv

fe[Kv]

para todouV. Y esto es lo que se deseaba.


29/94

22 AUTOSEMEJANZA

A continuacin vamos a definir la dimensin del multigrafo asociado a esta clase de conjuntos,para luego encontrar una frmula para el caso de dos nodos y finalmente damos un ejemplo paraaplicar los resultados de esta subseccin. En la seccin3.5vamos a necesitar esta dimensin paracalcular la dimensin Hausdorff de los conjuntos autosemejantes,(Kv)vV, que nos proporciona elteorema15.

Nmeros de Perron.. Para definir la dimensin de un grafo de Mauldin-Williams introduciremoslos nmeros de Perron". Consideraremos nicamente el caso cuando el grafo sea fuertemente

conectado y estrictamente contractivo.

Dado un grafo de Mauldin-Williams, sea s un nmero real positivo. En-

tonces los nmeros de Perron s-dimensionales para el grafo son nmeros

positivos qv, uno para cada nodo vV, tales que se cumpla:

qsu = vV

eEuv

r(e)s qsv

para todo uV.

Se puede probar bajo ciertas consideraciones sobre un grafo de Mauldin-Williams que existe un

nico nmero reals0 tal que los nmeros de Perronqvasociados al grafo existen. Este nmerosser utilizado para definir la dimensin del grafo. La existencia y unicidad de la dimensin sonprobadas en el teorema17.Pero antes, recordemos algunos resultados de lgebra lineal.SeaAuna matriz cuadrada. Elradio espectraldeA,R(A), es el mximo de los mdulos de todoslos valores propios deA. Tambin diremos que: A0 si todas las entradas de Ason no negativas,A >0 si todas las entradas deA son positivas. Una matriz A0 se dicereduciblesi por mediode permutaciones sobre las filas y las columnas, Ase puede escribir de la forma:

A=

B O

C D

dondeB y D son matrices cuadradas con al menos una fila cada una y Oes una matriz rectan-

gular de ceros. Si una matriz no es reducible, entonces se dice que es irreducible.Adems se necesita citar el teorema de Perron-Frobenius cuya prueba se puede encontrar en[15,cap. 13].

Teorema16. Sea A0una matriz cuadrada irreducible, y sea

. Entonces:

1. Si = R(A), entonces existe un vector columnax > 0con Ax= x .

2. Si existe un vector columnax 0 con Ax= x , entonces = R(A).3. Si existe un vector columnax 0 con Ax < x, entonces >R(A).4. Si existe un vector columnax 0 con Ax > x, entonces


30/94

23

para todo uV.Demostracin. Una prueba completa puede encontrarse en [9,p. 190]. En resumen esta pruebausa el hecho de que si A(s)es la matriz con entradas Auv(s) = eEuvr(e)

s y (s) = R(A(s))entoncesA(s)es irreducible s 0, pues si suponemos que A(s)es reducible, entonces debe tenerla siguiente forma:

A(s) =

B(s) O(s)C(s) D(s)

y si el grafo tienen nodos, u1, u2, . . . , uny en este mismo orden se describen las filas y columnasde A(s), entonces la matriz cuadrada B(s)es de orden k, donde 0 < k n 1. Al quedar el

bloque superior derecho de ceros, O(s),estonosdicequelosnodosu1, u2, . . . , ukpueden conectarsenicamente entre ellos mismos, lo que contradice que el grafo sea fuertemente conectado pues nose podr establecer un camino desde u1 hasta un. Usando el teorema16se prueba que (s)esuna funcin continua y que la ecuacin (s) = 1 tiene una solucin nica en el intervalo [0,[.Adems en esta demostracin se prueba que los nmeros de Perron existen si y solo si (s) =1.

El nmero s dado por el teorema anterior lo llamaremos la dimensin

del grafode Mauldin-Williams.

Si tomamos el caso de dos nodos podemos encontrar explcitamente la expresin para(s), ya quela matriz

A(s) =

A11(s) A12(s)A21(s) A22(s)

tiene polinomio caractersticopc() =2 traza(A(s)) +det(A(s))y los valores propios paraeste polinomio son

=12

traza(A(s))

(traza(A(s))2 4det(A(s))

ambos reales. Como necesitamos que p c(1) =0 tenemos queses la dimensin del grafo si:

1= A11(s) +A22(s) +

(A11(s) +A22(s))2

4(A11(s)A22(s) A12(s)A21(s))2 (1.15)

El Polvo en dos partes.. Considere el grafo definido por dos nodos{U, V}y cuatro aristasE ={a, b, c, d}y la lista de razonesra =1/2,rb =1/4,rc =1/2,rd = 3/4, descrito en la Figura1.8.Podemos aplicar los resultados de esta seccin encontrando una lista de conjuntos invariante.

Figura 1.8 Grafo para el Polvo en dos partes.

SeanU0,V0ambos como el segmento de lnea que une el punto (0, 0)con(1, 0). Sea la aplicacinade razn 12que fija el punto(0, 0)y rota 30

o. La aplicacinbde razn 14 que fija el punto (1, 0)yrota 60o. La aplicacincde razn 12 que fija el punto (0, 0)y rota 90o. Y por ltimo la aplicacin


31/94

24 AUTOSEMEJANZA

Figura 1.9 Construccin del Polvo en dos partes.

dde razn 34 que fija el punto (1, 0)y rota120o. Algebraicamente, para un punto(x,y) 2 seobtienen

a(x, y) = 1

4

3x y, x+

3y

b(x, y) = 1

8x

3y+7,

3 (1

x)

y

c(x, y) = 1

2(y, x)

d(x, y) = 3

8

113 x 3y,

3 (1 x)+y

Ahora defina recursivamente:

Un+1 = a[Un] b[Vn]Vn+1 = c[Un] d[Vn].

Esto define una sucesin de aproximaciones que son mostradas en la Figura1.9, ellas convergenen la mtrica Hausdorff aP; es ms, podemos empezar con cualesquiera dos conjuntos compactos

no vacosU0yV0en 2.

Figura 1.10 Polvo en dos partes.

Por el teorema15sabemos que existe un par de conjuntos compactos no vacos U,Vsubconjuntosde 2, satisfaciendo:

U = a[U] b[V]V = c[U] d[V]


32/94

25

A este par de conjuntosU, Vse le conoce como el Polvo en dos partes que denotamos porP, Figura1.10.Usando la igualdad (1.15) este grafo tiene dimensin 1. En este caso, los nmeros de Perron, unopara cada nodo, son qu = 1/3 y qv = 2/3. Lo importante acerca de estos nmeros es que sonpositivos y que satisfacen las ecuaciones:

qu =r(a)qu+r(b)qv

qv =r(c)qu+r(d)qv.


33/94

2 SISTEMAS DE

NUMERACIN

Algunos conjuntos se pueden ver como los atractores de un sistema iterado de funciones perotambin como el conjunto de elementos representables en un sistema de numeracin. Esto permiteestudiarlos desde otra perspectiva. En esta seccin se presentan algunos de estos conjuntos.

2.1 Bases para nmeros reales

Los enteros positivos se pueden representar en cualquier base enterab > 1 usando 0,1,..., b 1 como dgitos. Los sistemas decimal y binario son los ms conocidos. Los enteros positivos ynegativos se pueden representar en cualquier base b < 1, usando los dgitos desde 0 a |b| 1.Se generalizar esto; para ello se considera un nmero b con |b| > 1 como base, y un conjuntofinito de nmeros D ={d1, d2, , dk}, llamados dgitos", y se supone que 0 D. Los nmerosenteros" en esta base, son los que tienen la forma:

M

j=0

djbj (2.1)

conajD .Sea Wel conjunto formado por estos nmeros. Las fracciones" paraeste sistema tienenla forma:

1

j=djb

j (2.2)

con dj

D. Sea Fel conjunto formado por las fracciones. Un nmero arbitrariox

, repre-sentable en este sistema se puede ver como la suma de un entero y una fraccin, esto es

x=M

j=

djbj (2.3)

Es claro que para la convergencia de esta serie se debe tener que |b| > 1.


34/94

Teorema18. Sea b tal que|b| >1 y D ={d1, d2, , dk}. Entonces el conjunto F de las fraccioneses compacto y no vaco.

Demostracin. Considere las funciones fi(x) =d ib1 +b1x, como

|fi(x) fi(y)| =|b|1|x y|se tiene que son semejanzas en

2 de raznri =|b|1 1, y sea D un conjunto finito de nmeros reales que incluyen al cero.Entonces, o bien algunos nmeros reales no tienen representacin en la forma(2.3)o algunos nmeros reales

tienen ms de una expansin en la forma (2.3).

Demostracin. Vase [9,p. 84].

Lo que indica este teorema es que no existe una base en donde todos los nmeros complejos puedanser representados en forma nica.

2.2 Bases para nmeros complejos

Se dice que el entero Gaussianoz = x+iy con x , y se puede expresar en la base complejabsi este se puede escribir de la forma z = kr=0arb

r para algn k , donde los nmeros arson llamados los dgitos de la representacin, y se escribe z = (akak1. . . a0)b. El algoritmo para

27


35/94

28 SISTEMAS DE NUMERACIN

representar nmeros en una base entera se puede extender a bases complejas si el conjunto dedgitos escogidos forman un sistema completo de residuos mdulo el cuadrado del mdulo de la

base.Se dar un algoritmo para representar nmeros complejos en bases complejas, este algoritmo sedetermina para enteros Gaussianos.El siguiente teorema fundamenta el nmero de dgitos que debe tener una base para que se puedanrepresentar todos los nmeros complejos.

Teorema20. Sea b , sea D un conjunto finito de nmeros complejos que incluye al 0. Suponga que|D| = k, que todo nmero complejo se puede representar en este sistema y que la medida bidimensional deLebesgue del conjunto de los nmeros con mltiple representacin es 0. Entonces |b|2 =k.Demostracin. Como todo nmero complejo se puede representar en este sistema, se tiene que elconjunto de la fracciones F cumple con 0


36/94

29

Figura 2.1 Twindragon y teselacin fractal del plano.

a+bi n ir0

b na+nr0n2 + 1

s0i= :q1

donder0y s0son el residuo y el cociente de dividir a+nbpor n2 +1, recordando que el residuoes no negativo y menor que n2 +1. Se divide ahoraq1porn iy se obtiener1, siguiendo esteproceso, que paran ise sabe que es finito por ser buena base, hasta que qk = 0 se tiene quea+bi = (rkrk1. . . r0)ni. Como ejemplo, el nmero complejo6+31ise representa en la base2+icomo sigue:

6 + 31i 2 +i1 9 11i 2 +i

2 5 + 3i 2 +i1 3 + 0i 2 +i

3 0

as 6 + 31i= (3121)2+i, es decir 6 + 31i=3(2 + i)3 + 1(2 +i)2 + 2(2 +i)1 + 1(2 + i)0.Otras representaciones son por ejemplo:1 = (144)2+i, 8+3i = (1204)2+i, 5 = (1310)2+i, y10 = (133120)

2+i. De estas dos ltimas representaciones se pueden inferir las reglas de la suma

en esta base.Se considerarn algunas bases de nmeros complejos y se ver la forma que tiene el conjunto delas fracciones en esta base.Seab=1 + i, se ha mencionado que el conjunto de las fraccionesT, con los dgitos {0, 1} se llamaTwindragon. Este conjunto representa en el plano complejo todos los nmeros cuya representacines(0.a1a2. . . an. . . )1+i. Ver Figura2.1.Se puede cubrir el plano con una cantidad numerable de conjuntos idnticos a este conjunto, dela formaT+wdonde w es un entero gaussiano, y como todos los enteros gaussianos se puedenrepresentar en esta base, se puede obtener un mosaico o teselacin" fractal del plano, Figura 2.1derecha. Se dice fractal pues las fronteras de estos conjuntos son fractales[27], cuya dimensinfractal es aproximadamente 1.52.Con la baseb =1

i, aunque su conjunto de fracciones es simtrico a T, no se pueden representar

todos los enteros gaussianos, por ejemplo a 1:

1 = (1 i)(1 i) + 11 i = (i)(1 i) +0

i = (i)(1 i) +1i = (i)(1 i) +1


37/94


este procedimiento no es finito, de manera que no es posible representar a 1 en esta base con losdgitos 0 y 1.Ktai y Szab probaron en [24] que los nicos enteros gaussianos que pueden ser usados pararepresentar todos los nmeros complejos, usando nmeros naturales como dgitos son n+i yn iparanentero positivo. Parab = 2 icon D ={0,1,2,3,4}, la representacin del conjunto

Figura 2.2 Fracciones conb = 2 i

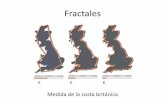
de las fracciones en el plano complejo es una curva dragn, Figura2.2. Mandelbrot la utiliz en[27]como un modelo para responder a la pregunta cunto mide la costa de Bretaa?

Figura 2.3 Fracciones conb =12+ 32 iy b =110+ i

Se pueden generar diferentes curvas dragn, considerando cualquier entero gaussiano como base,sin embargo, al considerar bases que no son de este tipo se obtienen conjuntos interesantes, porejemplo, al considerar como base b = 110 + i, el conjunto de las fracciones en esta base con D ={0, 1} se representa en el plano complejo en la Figura2.3derecha.Los conjuntos de fracciones en la Figura2.3, estn representados con los nmeros complejos cuyaexpansin binaria en estas bases es de la forma (0.a1a2. . . a14)b con ai {0, 1}, es decir, es unaaproximacin de los conjuntos reales. En algunos se muestran como figuras disconexas, sin em-

bargo, solamente parab=12+ 32 ilo es, en este caso se tiene que |b| 1.58 y en [3], se prueba quelos conjuntos de fracciones tales que |b| > 2 son totalmente disconexos.Usando el programaA.1.1,hecho enMathematica, se obtuvo la Figura2.2. Cambiando el conjuntode dgitos y la base, se obtienen las Figuras2.3,2.4.

2.4 Ejemplos de conjuntos de fracciones


38/94

31

En esta parte se presentarn diferentes tipos de conjuntos de fracciones que se obtienen de variarbases y sus conjuntos de dgitos; nos interesa los conjuntos de fracciones para nmeros reales ynmeros complejos.

Fracciones de Eisenstein.. Considere ahora dgitos complejos, por ejemplo D ={0,1, , 2}donde = 12 (1+i

3)y b =2 da una representacin de todos los nmeros complejos. Al

conjunto de todas las fracciones se le llama Fracciones de Eisenstein, Figura2.4.

Figura 2.4 Fracciones de Eisenstein

Note que este conjunto es el atractor para el sistema iterado de funciones definido por f0(x) =12 x,f1(x) = 12 (1+x), f2(x) = 12 (+x)y f3(x) = 12 (2 +x). La razn para estas funciones es|(2)1|= 12 , resolviendo la ecuacin 4( 12 )s =1 se tiene que la dimensin de semejanza es s = 2.Note que todos los dgitos no nulos tienen mdulo igual a 1.

El conjunto de Cantor como conjunto de fracciones.. Si se usan los dgitosD ={0,1,2}y labase b = 3, el conjunto de las fracciones es el intervalo[0, 1], as, la representacin tridica paracualquier x [0, 1]es (0.a1a2. . . ak. . . )3, con a i {0,1,2},i . En el teorema6del captuloanterior, se prob quex C si y solo si se puede representar en base 3 utilizando solamente 0 y 2

como dgitos.El tringulo de Sierpiski como conjunto de fracciones.. Al describir el tringulo de Sierpinski seus la representacin de las coordenadas del plano en base 2, esto nos permite dar una descripcinexacta de cules son puntos deS. Se puede encontrar un subconjunto de los nmeros complejosa partir de las coordenadas del tringulo de Sierpinski e identificar este conjunto con el tringulomismo, de esta manera si (x,y)son las coordenadas de un punto en S se dice que el nmerocomplejox +iypertenece al tringulo de Sierpinski. Si se usan los dgitos D ={0,1, i} conb = 2como base, se puede describir el conjunto de una forma sencilla.

Proposicin11. El conjunto de las fracciones de nmeros complejos para b = 2 y D ={0,1, i} es eltringulo de Sierpinski S.

Demostracin. Recordemos la construccin por tremas. Se empieza conS0, los vrtices de S0, son0, 1 e i. Como se reduce en cada paso de la construccin de Slos lados a la mitad, pertenecen12 = (0.1)2,

i2 = (0.i)2y

12 +

i2 = (0.1i)2en general al considerar las coordenadas de los puntos

(x,y)en su expansin en base 2, x = (0.a1a2 )2yy = (0.b1b2 )2conai, bi {0, 1}, i . Sesabe por el teorema11que todas las expansiones de las coordenadas no tienen un uno en la misma


39/94


posicin, por lo que se puede representar

x+iy =

k=1

(ak+ibk)2k

donde(ak+ibk)D .

Algunos nmeros del tringulo de Sierpinski son:

34

+i 18

= (0.110)2+ (0.00i)2= (0.11i)2

272341

+i68341

= (0.1100110000)2+ (0.00ii00ii00)2 = (0.11ii11ii00)2

79

+i1063

= (0.110001)2+ (0.00i0i0)2 = (0.11i0i1)2

38

+i1732

= (0.01100)2+ (0.i000i)2= (0.i110i)2

Es claro queSno va a rellenar el plano pues el nmero mnimo de dgitos que debe tener esta basepara que todo nmero complejo se pueda representar es 4, pues el teorema 20da una condicinnecesaria, adems 2 no es una buena base para los nmeros reales por lo que no ser til tampoco

para los complejos.

Otros conjuntos similares.. Si se completa el nmero de dgitos en la base 2 resultan conjuntosde fracciones que presentan alguna semejanza con el tringulo de Sierpinski pero que tampocopueden ser usados para representar a todos los nmeros complejos. Considere D ={0,1, i, 1}con b = 2. El conjunto de fracciones en esta base puede ser construido por tremas de la sigu-iente forma; tome un tringulo rectngulo issceles con la base en la hipotenusa, nase los puntosmedios de cada lado, el tringulo queda dividido en cuatro tringulos congruentes, elimine el in-terior del tringulo central y agrguese el tringulo formado por los puntos medios de las bases delos tringulos que han quedado, de la misma forma continese con el proceso en cada uno de loscuatro tringulos. El rea eliminada en cada paso es 18 del rea total por lo que tambin tiende acero.

Ahora se considerar el conjunto de los dgitos

D={0,1, i, 12

(1 +i)}

con la baseb =2, el nmero que se ha usado para completar tiene mdulo igual a 1 y se encuentraen el tercer cuadrante, el mdulo para los dgitos es 1 para los no nulos.El conjunto de las fracciones tambin se pueden construir por un proceso similar a los anteriores,solamente que en este caso se elimina tambin el tringulo central y se agrega el tringulo formadopor los puntos medios de los segmentos que forman cada vrtice con el circuncentro, cada uno deestos segmentos mide igual y el tringulo formado es semejante con razn de proporcin 12 . Enambos casos se tienen figuras en alguna forma parecidas al tringulo de Sierpinski, pero por la

base no se pueden representar todos los complejos.


40/94

3 DIMENSIN HAUSDORFFEn esta seccin se define un fractal en el sentido original de Mandelbrot. Esta se har comparando

la dimensin Hausdorff y una dimensin topolgica de un conjunto dado. La dimensin Haus-dorff fue introducida por Felix Hausdorff, en 1919, cuando trabaj con conjuntos de dimensinfraccionaria, mientras que la dimensin topolgica toma valores enteros o es infinita.

3.1 Dimensin topolgica

Aqu se define una dimensin topolgica, es decir, invariante bajo homeomorfismos, y se ver quese pueden caracterizar los conjuntos con dimensin cero.

Un subconjunto de un espacio mtrico se llama clopen1si es cerrado

y abierto, es decir, si su frontera es vaca. Adems se dice que un espa-

cio mtrico es cero-dimensionalsi existe una base para los abiertos

formada por conjuntos

A un espacio mtrico S, se le asocia un nmero entero o infinito, deno-

tada porind S, que se llama dimensin inductiva pequea y estdefinida recursivamente as: ind =1, para k 0 se dice queind S k si y solo si existe una base para los abiertos de S formada

por conjuntos U que cumplenind U k 1. As queind S = k siy solo si ind S k yind S k 1. Por ltimo siind S k no escierto para todo k, se dice queind S = .

Teorema21. Sean S y T espacios topolgicos. Si TS entonces ind Tind S y si S y T son homeomorfosentoncesind S = ind T.

1Contraccin del ingls closed and open"

33


41/94

34 DIMENSIN HAUSDORFF

Demostracin. [9,p. 82].

Teorema22. Si S es separable, entoncesind S = 0si y solo si S es homeomorfo a algn subconjunto de{0, 1}().Demostracin. Vase [9,p. 83].

En la proposicin9se prob que C, el conjunto de Cantor de los tercios centrales es homeomorfo a(E(),1/3)por lo que ind C =0. Todos los espacios que cumplen con el teorema22son llamadosgenricamente Conjuntos de Cantor", aunque no todos los conjuntos de Cantor tienen medida enel sentido de Lebesgue igual a cero, [48].

Proposicin12. El tringulo de Sierpinski S, cumpleind S =1.

Demostracin. Es claro que ind S no puede ser 2, pues el tringulo de Sierpinski no contiene aalguna bola de radio r > 0. Y no es 0 pues una base para los abiertos de Sformada por las in-tersecciones de S con cada tringulo deSn, no tienen frontera vaca, por lo que no son clopenes.

3.2 Generacin de medidas

En esta parte se recordarn algunos resultados sobre medidas. Estos se usarn para construir apartir de una funcin no negativa, una medida. Ser de utilidad especialmente para definir lamedida Hausdorff que se ocupar en3.3. Nos interesa este tipo de enfoque por su construccin.SeaXun conjunto cualquiera. Recordemos que siFes una -lgebra de subconjuntos de X, unamedidasobre Fes una funcin M :F [0,]que cumple lo siguiente

1.M() =0;2. SiAnes una sucesin disjunta de conjuntos, entonces

Mn An=

n=1 M(A

n)

(3.1)

Adems, siPdenota el conjunto de partes de X, una medida exterior sobre Xes una funcinM :P [0,]que satisface las siguientes condiciones

1.M() =0;2. SiAB, entonces M(A) M(B);3.M (n An) n=1 M(An).

Teorema23. Teorema del Mtodo I. Sea X un conjunto,A una familia de subconjuntos de X que locubren. Sea C :

A [0,]una funcin. Entonces, existe una nica medida exterior

Msobre X tal que

1.M(A)C(A)para todo A A,2. SiNes otra medida exterior sobre X conN(A)C(A)para todo A A, entoncesN(B) M(B)

para todo BX.Demostracin. [9,p. 134]. En esta prueba se da una frmula explcita para M. Si Des un cubrim-iento numerable deBcon subconjuntos de A, M(B) =infADC(A).


42/94

35

Una medida exterior M sobre un espacio mtrico(X,), se llamame-dida exterior mtricasiiM(A B) =M(A) + M(B)para con-

juntos A y B cuya distancia entre ellos es positiva. Se dice que esfinita

si M(A) < .

La razn de definir una medida exterior mtrica, y eventualmente una medida mtrica al restringira los conjuntos medibles, es porque todo conjunto de Borel es medible, hecho que no se cumple

con cualquier medida exterior.Teorema24. SeaM una medida exterior mtrica sobre un espacio mtrico S, entonces todo conjunto deBorel en S es M-medible.Demostracin. Vase [9,p. 138].

Si M es una medida mtrica finita sobre un espacio mtrico compactoS, se puede probar queM(E) =inf{M(U): EU, abierto}

ademsM(E) =sup{M(K): KE, compacto}

para todo conjunto medibleES, as que dado > 0 existe un conjunto compacto Ky un abiertoUconKEUtal que M(U\ K) < para todo > 0, pues M(U) 2 < M(E) < M(K) + 2ycomo M(K) + M(U\ K) =M(U) < M(K) + de donde M(U\ K) < . Esto dice que para todoconjunto medible, se pueden encontrar un conjunto compactoKy un abiertoUconKEUtalque la medida de su diferencia es tan pequea como se quiera.

Mtodo II.. Este es ms complicado que el Mtodo I, pero lo importante es que se construye unamedida exterior mtrica.

Proposicin13. Sean A Bdos cubrimientos de X y C :B [0,]una funcin sobre conjuntos dada.Si M es la medida exterior sobre X definida a partir del Mtodo I, teorema23,por C y A, y siNes la medidaexterior sobre X definida a partir del Mtodo I por C y BentoncesN(A) M(A)para todo AX.Demostracin. Sea Dun cubrimiento numerable de A, por el teorema23tenemos

M(B) =infAD

C(A),

como Des un cubrimiento numerable de Bse tiene queN(B) =infADC(A)y como el nfimose toma uno sobre un subconjunto del otro, se tiene queN(B) M(B).

SeaAuna familia de subconjuntos de un espacio mtrico S. Supongaque para todo xS y > 0existe A A con x A ydiam A.Suponga que C :A [0,]es una funcin sobre conjuntos dada. SeaA ={A A : diam A }. SeaM la medida exterior sobre Xdefinida a partir del Mtodo I por C y

A. Se define

M(E) =lim0

M(E) =sup>0

M(E)

de esta forma M es una medida exterior. A esta construccin se le llamaelMtodo II.


43/94

36 DIMENSIN HAUSDORFF

Teorema25. La funcin sobre conjuntos M definida por el Mtodo II es una medida exterior mtrica.Demostracin. Vase [9,p. 141].

Teorema26. Sea E() un espacio de hileras infinitas. Suponga que nmeros no negativos w satisfacenw = eEweparaE(). Entonces la medida exterior, M, definida por el teorema23para la funcinsobre conjuntos C([]) =wes una medida exterior mtrica sobre E() que cumple con M([]) =w. As0 < M(E()) < .Demostracin. Vase [9,p. 143].

3.3 Medida Hausdorff

Sea S un espacio mtrico y s un nmero positivo. La medida exte-

rior Hausdorff s-dimensionales la medida exterior definida por el

mtodo II, a partir de la funcin sobre conjuntos C(A) =diam (A)s,la cual se denota por Hs. La restriccin a los conjuntos medibles es lla-

mada medida Hausdorff s-dimensional, y se escribe Hs

.

Dado queHs es construido por el mtodo II, esta es una medida exterior mtrica. As en partic-ular, todo conjunto de Borel es medible (abiertos, cerrados, compactos etc.). El teorema 23da unafrmula explcita de la definicin.

Sea un nmero positivo. El cubrimientoAes un -cubrimiento si ysolo si eldiam (A) para todo A A. En este caso defina:

Hs (F) =infAA

diam (A)s (3.2)

donde el nfimo se toma sobre todos los -cubrimientos numerablesAde F.

Obsrvese que si 1 2entonces Hs

Fractales - Manuel Alfaro A, Manuel Murrilo T. , Alberto Soto A..pdf

Documents

Transcript of Fractales - Manuel Alfaro A, Manuel Murrilo T. , Alberto Soto A..pdf