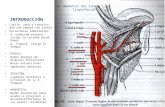
Práctica 7 INTERPOLACIÓN 5.1. Interpolación Polinómicajomalapa/Practicas AYMN...

Práctica 7INTERPOLACIÓN

5.1. Interpolación Polinómica ü Datos de interpolación: 8Hxk, fkL<k=0,1,...,n

Conocemos los valores de una función, fk = f HxkL, en n + 1 puntos distintos, xk, de un intervalo [a,b]

ü Funciones interpolantes: Polinomios de grado menor o igual que n

(1)p HxL = a0 + a1 x + a2 x2 + ... + an xn

ü Problema de interpolación: Determinar los coeficientes a0, a1, ... , an para que se cumplan las condiciones de interpolación:

(2)p HxkL = fk, k = 0, 1, ..., n

Método de CramerConsiste en escribir el polinomio p(x) en la forma (1). Al imponer las condiciones de interpolación dadas en(2) se obtiene un sistema de (n+1)×(n+1) ecuaciones lineales. La solución del sistema nos permite calcularlos coeficientes ak, k = 0, 1, ... , n.

à EJEMPLO 1Determinar el polinomio que interpola al conjunto de datos

{(0,-3),(3,5),(4,8),(5,18),(6,-2)}

ü Datos de interpolación

puntos := 880, −3<, 83, 5<, 84, 8<, 85, 18<, 86, −2<<ü Función interpolante: (polinomio de grado 4 porque tenemos 5 datos de interpolación)

p@x_D := a0 + a1 x + a2 x2 + a3 x3 + a4 x4

Practica7.nb 1

ü Condiciones de interpolación

ecu1 = p@0D −3

a0 -3

ecu2 = p@3D 5

a0 + 3 a1 + 9 a2 + 27 a3 + 81 a4 5

ecu3 = p@4D 8

a0 + 4 a1 + 16 a2 + 64 a3 + 256 a4 8

ecu4 = p@5D 18

a0 + 5 a1 + 25 a2 + 125 a3 + 625 a4 18

ecu5 = p@6D −2

a0 + 6 a1 + 36 a2 + 216 a3 + 1296 a4 -2

ü Solución del sistema de ecuaciones

coef = Solve@8ecu1, ecu2, ecu3, ecu4, ecu5<D99a0 Ø -3, a1 Ø

4747ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ

60, a2 Ø -

7003ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ120

, a3 Ø863ÅÅÅÅÅÅÅÅÅÅÅÅÅ60

, a4 Ø -137ÅÅÅÅÅÅÅÅÅÅÅÅÅ120

==ü Polinomio solución (sustituimos el valor de los coeficientes obtenidos en la expresión de p[x])

polisolu = p@xD ê. coef@@1DD-

137 x4ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ

120+

863 x3ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ

60-

7003 x2ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ

120+

4747 xÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ

60- 3

Practica7.nb 2

ü Visualización de resultados

g1 = ListPlot@puntos, PlotStyle → [email protected],DisplayFunction → IdentityD;

g2 =

Plot@polisolu, 8x, −0.2, 6.2<, DisplayFunction → IdentityD;Show@g1, g2, DisplayFunction → $DisplayFunctionD;

1 2 3 4 5 6

-20

-10

10

20

30

Método de LagrangeConsiste en calcular previamente los polinomios LiHxL, i=0,1,...,n, llamados polinomio deLagrange o funciones cardinales de Lagrange, que verifican:

Li HxiL = 1, Li HxjL = 0, i ≠ j

Estos polinomios vienen dados por la expresión

Li HxL = ‰j=0j≠i

n x − xjxi − xj

El polinomio de interpolación se escribe entonces en la forma

p HxL = f0 L0 HxL + f1 L1 HxL + ... + fn Ln HxL = ‚i=0

nfi Li HxL

à EJEMPLO 2Calcular el polinomio que interpola al conjunto de datos

{(-1,2),(2,8),(5,-3), (8,10)}

Los nodos de interpolación son los puntos:

x0 = −1, x1 = 2, x2 = 5, x3 = 8

Practica7.nb 3

ü Definimos los puntos

puntos := 88−1, 2<, 82, 8<, 85, −3<, 88, 10<<ü Definimos los nodos

x0 = −1; x1 = 2; x2 = 5; x3 = 8;

f0 = 2; f1 = 8; f2 = −3; f3 = 10;

ü Calculamos los polinomios de Lagrange

L0@x_D =Hx − x1L Hx − x2L Hx − x3LHx0 − x1L Hx0 − x2L Hx0 − x3L

-1

ÅÅÅÅÅÅÅÅÅÅÅÅÅ162

Hx - 8L Hx - 5L Hx - 2LL1@x_D =

Hx − x0L Hx − x2L Hx − x3LHx1 − x0L Hx1 − x2L Hx1 − x3L1

ÅÅÅÅÅÅÅÅÅ54

Hx - 8L Hx - 5L Hx + 1LL2@x_D =

Hx − x0L Hx − x1L Hx − x3LHx2 − x0L Hx2 − x1L Hx2 − x3L-

1ÅÅÅÅÅÅÅÅÅ54

Hx - 8L Hx - 2L Hx + 1LL3@x_D =

Hx − x0L Hx − x1L Hx − x2LHx3 − x0L Hx3 − x1L Hx3 − x2L1


Hx - 5L Hx - 2L Hx + 1L

Practica7.nb 4

ü Cálculo del polinomio de inteprolación

polisolu = f0 L0@xD + f1 L1@xD + f2 L2@xD + f3 L3@xD-


Hx - 8L Hx - 5L Hx - 2L +1


Hx - 8L Hx + 1L Hx - 2L +


Hx - 5L Hx + 1L Hx - 2L +4


Hx - 8L Hx - 5L Hx + 1Lü Visualización de resultados

g1 = ListPlot@puntos, PlotStyle → [email protected],DisplayFunction → IdentityD;

g2 = Plot@polisolu, 8x, −1.2, 8.2<,DisplayFunction → IdentityD;

Show@g1, g2, DisplayFunction → $DisplayFunctionD;

2 4 6 8-2.5

2.5

5

7.5

10

12.5

Método de Newton (Diferencias divididas)Consiste en escribir el polinomio de interpolación en la forma:

p HxL = A0 + A1 Hx − x0L + A2 Hx − x0 Hx − x1L + ... + An−1 Hx − x0 Hx − x1L ... Hx − xn−1LLos coeficientesAk , que se denominan diferencias divididas de la función f en los puntos x0, x1, ... xk , se denotan por Ak= f[x0, x1, ... xk] y se generan de forma recursiva mediante la fórmula

f@x0, x1, ... xkD =f@x1, x2, ... xkD − f@x0, x1, ... xk−1DHxk − x0L , k = 1, 2, ..., n

partiendo de f[x0]=f(x0).

Con esta notación, el polinomio de interpolación puede escribirse como

Practica7.nb 5

p HxL = f@x0D + f@x0, x1D Hx − x0L + f@x0, x1, x2D Hx − x0L Hx − x1L + ... +

f@x0, x1, ..., xnD Hx − x0L Hx − x1L ... Hx − xn−1L.à EJEMPLO 3

Calcular el polinomio que interpola al conjunto de datos8H−5, 1L, H−3, 2L, H2, 10L, H3, 2L, H6, 0L, H8, −3L<ü Entrada de datos

puntos = 88−5, 1<, 8−3, 2<, 82, 10<, 83, 2<, 86, 0<, 88, −3<<;ü Determinamos los nodos y los valores de la función

n = Length@puntosD − 1;For@i = 0, i ≤ n, i++,xi = puntos@@i + 1, 1DD; fi = puntos@@i + 1, 2DDD

ü Generamos la tabla de diferencias divididas (creamos una matriz rectangular de orden (2n+2)× (n+2) que llamanos dif y cuyos elementos son de la forma d[i,j], con i=-1,0,…,2n y j=-1,0,…, n.

Clear@dD;dif = Array@d, 82 n + 2, n + 2<, −1Di

k

jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjj

dH-1, -1L dH-1, 0L dH-1, 1L dH-1, 2L dH-1, 3L dH-1, 4L dH-1, 5LdH0, -1L dH0, 0L dH0, 1L dH0, 2L dH0, 3L dH0, 4L dH0, 5LdH1, -1L dH1, 0L dH1, 1L dH1, 2L dH1, 3L dH1, 4L dH1, 5LdH2, -1L dH2, 0L dH2, 1L dH2, 2L dH2, 3L dH2, 4L dH2, 5LdH3, -1L dH3, 0L dH3, 1L dH3, 2L dH3, 3L dH3, 4L dH3, 5LdH4, -1L dH4, 0L dH4, 1L dH4, 2L dH4, 3L dH4, 4L dH4, 5LdH5, -1L dH5, 0L dH5, 1L dH5, 2L dH5, 3L dH5, 4L dH5, 5LdH6, -1L dH6, 0L dH6, 1L dH6, 2L dH6, 3L dH6, 4L dH6, 5LdH7, -1L dH7, 0L dH7, 1L dH7, 2L dH7, 3L dH7, 4L dH7, 5LdH8, -1L dH8, 0L dH8, 1L dH8, 2L dH8, 3L dH8, 4L dH8, 5LdH9, -1L dH9, 0L dH9, 1L dH9, 2L dH9, 3L dH9, 4L dH9, 5LdH10, -1L dH10, 0L dH10, 1L dH10, 2L dH10, 3L dH10, 4L dH10, 5L

y

{

zzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzA continuación rellenamos la matriz con espacios

For@i = −1, i ≤ 2 n, i++, For@j = −1, j ≤ n, j++,d@i, jD = ""DD

Para visualizar el resultado basta con escribir dif y pulsar intro

Practica7.nb 6

difi

k


y

{

zzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzAhora rellenamos la primera y segunda filas (fila -1 y fila 0, respectivamente) con los datos deinterpolación y ponemos de cabecera el texto “xk” y “ fk” en la posición (-1,-1) y (-1,0) , respectivamente.

d@−1, −1D = "xk"; d@−1, 0D = "fk";For@i = 0, i ≤ n + 1, i++, d@2 i, −1D = xi; d@2 i, 0D = fiD;

Veamos el resultado

difi

k


xk fk-5 1

-3 2

2 10

3 2

6 0

8 -3

y

{

zzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzFinalmente calculamos los restantes elementos de la tabla aplicando la ley de recurrencia

ForAj = 1, j ≤ n, j++, ForAi = j, i ≤ 2 n − j, i = i + 2,

d@i, jD =d@i + 1, j − 1D − d@i − 1, j − 1Dd@i + j, −1D − d@i − j, −1D EE

Practica7.nb 7

Visualizamos el resultado final

difi

k

jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjj

xk fk-5 1

1ÅÅÅÅ2

-3 2 11ÅÅÅÅÅÅÅ708ÅÅÅÅ5 - 123ÅÅÅÅÅÅÅÅÅÅ560

2 10 - 8ÅÅÅÅ59089ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ166320

-8 103ÅÅÅÅÅÅÅÅÅÅ270 - 19897ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ2162160

3 2 11ÅÅÅÅÅÅÅ6 - 193ÅÅÅÅÅÅÅÅÅÅÅÅ2970

- 2ÅÅÅÅ3 - 1ÅÅÅÅ3

6 0 - 1ÅÅÅÅ6

- 3ÅÅÅÅ28 -3

y

{

zzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzCalculamos el polinomio de interpolación

polisolu = „k=0

n

d@k, kD ikjjjjjj‰j=0

k−1Hx − xjLy{zzzzzz-

19897 Hx - 6L Hx - 3L Hx - 2L Hx + 3L Hx + 5LÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ

2162160+

9089 Hx - 3L Hx - 2L Hx + 3L Hx + 5LÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ

166320-

123ÅÅÅÅÅÅÅÅÅÅÅÅÅ560

Hx - 2L Hx + 3L Hx + 5L +11ÅÅÅÅÅÅÅÅÅ70

Hx + 3L Hx + 5L +x + 5ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ

2+ 1

Visualizamos el resultado (en las variables xmin y xmax, guardamoe el valor mínimo y máximo de losnodos)

Practica7.nb 8

xmin = Min@Table@xi, 8i, 0, n<DD;xmax = Max@Table@xi, 8i, 0, n<DD;g1 = ListPlot@puntos,

PlotStyle → [email protected], DisplayFunction → IdentityD;g2 = Plot@polisolu, 8x, xmin − 0.2, xmax + 0.2<,

DisplayFunction → IdentityD;Show@g1, g2, DisplayFunction → $DisplayFunctionD;

-4 -2 2 4 6 8-5

5

10

15

20

5.2. Interpolación polinómica con MathematicaEl programa Mathematica puede calcular directamente el polinomio de interpolación mediante la instrucción:

ü InterpolatingPolynomial[puntos, variable] Calcula el polinomio de interpolación en la variable especificada para el conjunto de puntos dados en laforma:

puntos=88x0, f0<, 8x1, f1<, ..., 8xn, fn<<. à EJEMPLO 4

Determinar el polinomio que interpola al conjunto de puntos

{ (0,0), (3,2), (5,2), (7,3), (9,5), (11,3) }

ü Introducimos los datos

puntos := 880, 0<, 83, 2<, 85, 2<, 87, 3<, 89, 5<, 811, 3<<

Practica7.nb 9

ü Calculamos el polinomio

p@x_D = InterpolatingPolynomial@puntos, xDJJJJ-

1079 Hx - 9LÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ

1330560-

31ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ7560

N Hx - 7L +31


N Hx - 5L -2


N Hx - 3L +2ÅÅÅÅÅ3

N x

Expand@%D-

1079 x5ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ1330560

+73 x4ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ4752

-9133 x3ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ133056

-553 x2ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ4752

+569683 xÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ443520

ü Visualizamos resultados

grafpuntos = ListPlot@puntos,PlotStyle −> [email protected], DisplayFunction → IdentityD;

grafpoli = Plot@p@xD, 8x, −0.5, 11.5<,DisplayFunction → IdentityD;

Show@grafpuntos, grafpoli,DisplayFunction → $DisplayFunctionD;

2 4 6 8 10

1

2

3

4

5

5.3. Interpolación con funciones splines Sea D una partición del intervalo [a,b],

∆ : a = x0 < x1 < ... < xn = b.Un spline es una función polinómica a trozos en cada uno de los intervalos [xi, xi+1] de la partición.

Practica7.nb 10

Notaremos por Smk HDL al conjunto de funciones de clase k que son polinomios a trozos de grado m en cada

uno de los intervalos de la partición:

Snk H∆L = 8s ∈ Cmk H@a, bDL : s »@xi,xi+1D ∈ m<,donde m denota el conjunto de polinomios de grado a lo sumo m.

En lo sucesivo notaremos:D={x0, x1, ... , xn} la partición dada por los nodos. hi = xi+1 - xi, a la amplitud del intervalo [xi, xi+1]. fi a los valores de la función que queremos interpolar. mi = H fi+1 - fiL ê hi, a la pendiente de la curva en el intervalo [xi, xi+1].

Interpolación lineal a trozos

ü Funciones interpolantes: Splines en S10 HDL. Se trata de funciones continuas definidas a trozos

mediante polinomios de grado 1 en cada intervalo de la partición.

ü Problema de interpolación: Determinar un spline s œ S10HDL tal que:

s HxiL = fi, i = 0, 1, ..., n

ü Solución del problema: Si denotamos por si HxL a la restricción del spline s al intervalo [xi, xi+1], entonces

si HxL = fi + mi Hx − xiL, i = 0, 1, ..., n,

es la recta que pasa por los puntos Hxi, fiL y Hxi+1, fi+1L.à EJEMPLO 5

Determinar el spline lineal que interpola al conjunto de datos

{(0,0), (3,1.2), (5,1.7), (7,2.0), (9,2.1), (11,2.0), (12, 1.8), (13,1.2), (14,1.0), (15,1.6)}

ü Introducimos los datos

puntos := 880, 0<, 83, 1.2<, 85, 1.7<, 87, 2.0<, 89, 2.1<,811, 2.0<, 812, 1.8<, 813, 1.2<, 814, 1.0<, 815, 1.6<<ü Definimos las variables

n = Length@puntosD − 1;For@i = 0, i ≤ n, i++,xi = puntos@@i + 1, 1DD; fi = puntos@@i + 1, 2DDD;

ForAi = 0, i ≤ n − 1, i++, hi = xi+1 − xi; mi =fi+1 − fi

hiE;

Practica7.nb 11

ü Determinamos el spline

For@i = 0, i ≤ n − 1, i++, si@x_D = fi + mi Hx − xiLDü Visualizamos resultados

grafpuntos = ListPlot@puntos,PlotStyle → [email protected], DisplayFunction → IdentityD;

For@i = 0, i ≤ n − 1, i++, gi = Plot@si@tD,8t, xi, xi+1<, DisplayFunction → IdentityDD;Show@grafpuntos, Table@gi, 8i, 0, n − 1<D,DisplayFunction → $DisplayFunctionD;

2 4 6 8 10 12 14

0.5

1

1.5

2

Interpolación con splines cúbicos: S32HDL

ü Funciones interpolantes: Splines en S32 HDL. Se trata de funciones de clase 2 definidas a trozos

mediante polinomios de grado 3 en cada intervalo de la partición.

ü Problema de interpolación: Determinar un spline s Œ S32 HDL tal que:

s HxiL = fi , i = 0, 1, ..., n,

à EJEMPLO 6Calcular el spline cúbico natural que interpola al conjunto de datos :

{(-1,0), (3,1), (5,-3), (7,2)} ,

En este caso el spline será una función de clase 2 definida a trozos, mediante 3 polinomios de tercer grado,que escribiremos en la forma

s HxL =

ikjjjjjjjjjjj

a0 + b0 Hx + 1L + c0 Hx + 1L2 + d0 Hx + 1L3, x œ @-1, 3La1 + b1 Hx - 3L + c1 Hx - 3L2 + d1 Hx - 3L3, x œ @3, 5La2 + b2 Hx - 5L + c2 Hx - 5L2 + d2 Hx + 5L3, x œ @5, 7D

Practica7.nb 12

con las condiciones adicionales: s '' Hx0L = s '' HxnL = 0

ü Definimos los puntos

puntos = 88−1, 0<, 83, 1<, 85, −3<, 87, 2<<;ü Definimos cada uno de los trozos que definen el spline

s0@x_D := a0 + b0 Hx + 1L + c0 Hx + 1L2 + d0 Hx + 1L3;s1@x_D := a1 + b1 Hx − 3L + c1 Hx − 3L2 + d1 Hx − 3L3;s2@x_D := a2 + b2 Hx − 5L + c2 Hx − 5L2 + d2 Hx − 5L3

ü Imponemos las condiciones de interpolación

ecu1 = s0@−1D 0

a0 0

ecu2 = s1@3D 1

a1 1

ecu3 = s2@5D −3

a2 -3

ecu4 = s2@7D 2

a2 + 2 b2 + 4 c2 + 8 d2 2

ü Imponemos las condiciones de continuidad (en nodos interiores)

ecu5 = s0@3D s1@3Da0 + 4 b0 + 16 c0 + 64 d0 a1

Practica7.nb 13

ecu6 = s1@5D s2@5Da1 + 2 b1 + 4 c1 + 8 d1 a2

ü Imponemos las condiciones de derivabilidad: clase 1 (en nodos interiores)

ecu7 = s0'@3D s1'@3Db0 + 8 c0 + 48 d0 b1

ecu8 = s1'@5D s2'@5Db1 + 4 c1 + 12 d1 b2

ü Imponemos las condiciones de derivabilidad: clase 2 (en nodos interiores)

ecu9 = s0''@3D s1''@3D2 c0 + 24 d0 2 c1

ecu10 = s1''@5D s2''@5D2 c1 + 12 d1 2 c2

ü Imponemos la condición en la frontera s''(-1)=s''(7)=0

ecu11 = s0''@−1D 0

2 c0 0

ecu12 = s2''@7D 0

2 c2 + 12 d2 0

Practica7.nb 14

ü Resolvemos el sistema formado por todas las ecuaciones

coeficientes = Solve@8ecu1, ecu2, ecu3, ecu4,ecu5, ecu6, ecu7, ecu8, ecu9, ecu10, ecu11, ecu12<D

99a0 Ø 0, a1 Ø 1, a2 Ø -3, c0 Ø 0, c1 Ø -81ÅÅÅÅÅÅÅÅÅ92

, d0 Ø -27


, b0 Ø131ÅÅÅÅÅÅÅÅÅÅÅÅÅ92

,

b1 Ø -193ÅÅÅÅÅÅÅÅÅÅÅÅÅ92

, c2 Ø351ÅÅÅÅÅÅÅÅÅÅÅÅÅ184

, d1 Ø171ÅÅÅÅÅÅÅÅÅÅÅÅÅ368

, b2 Ø -1


, d2 Ø -117ÅÅÅÅÅÅÅÅÅÅÅÅÅ368

==ü Sustituimos los coeficientes en las expresiones de s0HxL, s1HxL y s2HxL

sp0@x_D = s0@xD ê. coeficientes@@1DD131 Hx + 1LÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ

92-


Hx + 1L3

sp1@x_D = s1@xD ê. coeficientes@@1DD171ÅÅÅÅÅÅÅÅÅÅÅÅÅ368

Hx - 3L3 -81ÅÅÅÅÅÅÅÅÅ92

Hx - 3L2 -193 Hx - 3LÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ

92+ 1

sp2@x_D = s2@xD ê. coeficientes@@1DD-


Hx - 5L3 +351ÅÅÅÅÅÅÅÅÅÅÅÅÅ184

Hx - 5L2 +5 - xÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ

23- 3

Nuestra función spline vendrá dada por

s@x_D :=

Which@−1 ≤ x < 3, sp0@xD, 3 ≤ x < 5, sp1@xD, 5 ≤ x ≤ 7, sp2@xDD

Practica7.nb 15

ü Visualizamos los resultados

grafpuntos = ListPlot@puntos,PlotStyle → [email protected], DisplayFunction → IdentityD;

grafspline = Plot@s@xD, 8x, −1, 7<,DisplayFunction → IdentityD;

Show@grafpuntos, grafspline,DisplayFunction → $DisplayFunctionD;

2 4 6

-3

-2

-1

1

2

Interpolación con funciones splines en MathematicaEl programa Mathematica incorpora dos instrucciones que nos permiten calcular directamente el splinelineal a trozos y el spline cúbico natural que interpolan a un conjunto de puntos.

La instrucción: Interpolation[puntos, InterpolationOrder→1]Calcula el spline lineal a trozos que interpola al conjunto de puntos dados mediante una tabla del tipo

puntos = 88x0, f0<, 8x1, f1<, ..., 8xn, fn<<à EJEMPLO 7

Determinar el spline lineal a trozos que interpola al conjunto de datos

{(0,0), (3,1.2), (5,1.7), (7,2.0), (9,2.1), (11,2.0), (12, 1.8), (13,1.2), (14,1.0), (15,1.6)}

puntos := 880, 0<, 83, 1.2<, 85, 1.7<, 87, 2.0<, 89, 2.1<,811, 2.0<, 812, 1.8<, 813, 1.2<, 814, 1.0<, 815, 1.6<<

Practica7.nb 16

ü Determinamos el spline

s = Interpolation@puntos, InterpolationOrder → 1DInterpolatingFunction@H 0. 15. L, <>D

Observemos que al definir la función s no ha sido necesario indicar la variable. Sin embargo, a partir deeste momento podemos utlizar la función s(x), como si se tratara de cualquier función definida por elusuario que sólo está definida en el intervalo [0,15]. Notemos también que el programa tampoco nos dala expresión explícita de la función s(x).

ü Visualizamos resultados


grafspline = Plot@s@xD, 8x, 0, 15<,DisplayFunction → IdentityD;


2 4 6 8 10 12 14

0.5

1

1.5

2

La instrucción: SplineFit[puntos, Cubic]Calcula el spline lineal cúbico natura que interpola al conjunto de puntos dados mediante una tabla del tipo

puntos = 88x0, f0<, 8x1, f1<, ..., 8xn, fn<<IMPORTANTE:

ü Para utilizar la instrucción SplineFit hemos de cargar previamente el paquete

NumericalMath`SplineFit`

Practica7.nb 17

ü La instrucción SplineFit genera una curva dada en forma paramétrica: s(t)=(x(t),y(t)), con tœ[0,n], de forma que s(i)=(xi, fi), i=0,1, ..., n.

à EJEMPLO 8Determinar el spline cúbico natural que interpola al conjunto de datos

{(0,0), (3,1.2), (5,1.7), (7,2.0), (9,2.1), (11,2.0), (12, 1.8), (13,1.2), (14,1.0), (15,1.6)}

ü Cargamos el paquete

<< NumericalMath`SplineFit`

ü Definimos los puntos que queremos interpolar

puntos := 880, 0<, 83, 1.2<, 85, 1.7<, 87, 2.0<, 89, 2.1<,811, 2.0<, 812, 1.8<, 813, 1.2<, 814, 1.0<, 815, 1.6<<ü Calculamos el spline cúbico

sc = SplineFit@puntos, CubicDSplineFunction@Cubic, 80., 9.<, <>D

Mathematica no nos devuelve una función real de variable real sino una curva en forma paramétrica, paravalores del parámetro tœ[0,9] (esto significa que el spline se ha construido en 10 puntos numerados delcero al nueve).

Practica7.nb 18

ü Visualizamos el resultado (observemos que tenemos que utilizar la instrucción ParametricPlot para representar la gráfica del spline entre los nodos 0 y 9); si queremos dibujar la gráfica del spline entre los nodos 3 y 5 basta sustituir en {t,0,9} por {t,3,5}. Si no se incluye CompiledÆFalse Mathematica intenta usar una función compilada y produce un mensaje de advertencia indicando que no es posible y que utilizará una función no compilada.


grafspline = ParametricPlot@sc@tD, 8t, 0, 9<,Compiled → False, DisplayFunction → IdentityD;


2 4 6 8 10 12 14

0.5

1

1.5

2

El obtener una curva en forma paramétrica nos sugiere que se pueden utilizar como datos deinterpolación puntos cualesquiera del plano y obtener distintos tipos de curvas.

Veamos otros ejemplos:

sp1 = SplineFit@880, 1<, 81, 1<, 81, −1<, 80, −1<<, CubicDSplineFunction@Cubic, 80., 3.<, <>D

Practica7.nb 19

grafsp1 = ParametricPlot@sp1@tD,8t, 0, 3<, PlotRange → All, Compiled → FalseD;

0.2 0.4 0.6 0.8 1

-1

-0.5

0.5

1

sp2 =

SplineFit@880, −1<, 80, 1<, 81, 1<, 81, −1<, 80, −1<<, CubicDSplineFunction@Cubic, 80., 4.<, <>Dgrafsp2 = ParametricPlot@sp2@tD,8t, 0, 4<, PlotRange → All, Compiled → FalseD;

0.2 0.4 0.6 0.8 1 1.2

-1

-0.5

0.5

1

sp3 = SplineFit@88−2.5, 1<, 8−1.25, −1<,80., 1<, 81.25, −1<, 82.5, 1<<, CubicDSplineFunction@Cubic, 80., 4.<, <>D

Practica7.nb 20

grafsp3 = ParametricPlot@sp3@tD,8t, 0, 4<, PlotRange → All, Compiled → FalseD;

-2 -1 1 2

-1

-0.5

0.5

1

¿Cómo podemos saber cual es la expresión de los polinomios que forman la función spline resultante?.La salida que ha generado Mathematica con sp3 puede ser examinada con la instrucción InputFormcuya sintasis en este caso es:

InputForm[sp3]

InputForm@sp3DSplineFunction[Cubic, {0., 4.}, {{-2.5, 1}, {-1.25, -1}, {0., 1}, {1.25, -1}, {2.5, 1}}, {{{-2.5, 1.25, 2.220446049250313*^-16, -2.220446049250313*^-16}, {1, -24/7, 0, 10/7}}, {{-1.25, 1.2499999999999998, 2.220446049250313*^-16, 0.}, {-1, 6/7, 30/7, -22/7}}, {{0., 1.2500000000000002, -4.440892098500626*^-16, 2.220446049250313*^-16}, {1, 0, -36/7, 22/7}}, {{1.25, 1.25, 0., 0.}, {-1, -6/7, 30/7, -10/7}}}]

La salida nos indica: que es un spline cúbico construido a partir de 5 datos, la tercera componente {-2.5,1}, {-1.25, -1}, {0., 1}, {1.25, -1}, {2.5, 1} son los puntos que se han utilizado, en la cuarta componentehay una lista formada por cuatro listas , cada una de ellas con dos sublistas:

la primera lista {{-2.5, 1.25, 2.220446049250313*^-16, -2.220446049250313*^-16}, {1, -24/7, 0,10/7}} significa que en el intervalo que tiene de extremo de la izquierda -2.5, es decir, en [-2.5, -1.25] elspline cúbico es la función polinómica

1- 24ÄÄÄÄÄÄÄ7 x + 0 x2 + 10ÄÄÄÄÄÄÄ7 x3

la última lista {{1.25, 1.25, 0., 0.}, {-1, -6/7, 30/7, -10/7}}}significa que en el intervalo que tiene deextremo de la izquierda 1.25, es decir, en [1.25, 2.5] el spline cúbico es la función polinómica

-1- 6ÄÄÄÄ7 x + 30ÄÄÄÄÄÄÄ7 x2 - 10ÄÄÄÄÄÄÄ7 x3

Practica7.nb 21

Ejercicios propuestos 1. Calcula, usando diferencias divididas el polinomio p(x) que interpola a la función f(x)=sen x en los puntos que resultan de dividir el intervalo [0,2p] en 8 partes iguales.

Dibuja en unos mismos ejes coordenados y con diferente color la gráfica de la función y del polinomio

2. Los datos correspondientes al censo de una población (en miles de habitantes) se recogen en la siguiente tabla:

Año 1950 1960 1970 1980 1990 2000Número habitantes 123.5 131.2 150.7 141.3 203.2 240.5

a) Utilizar interpolación polinómica para estimar el número de habitantes en el año 1965.b) ¿Cuál será la población estimada para el año 2020?. Comenta el resultado.

3. Determinar el spline cúbico sujeto para el conjunto de puntos

{(0,1), (1,3), (2,5), (5,8), (7,3), (10,0), (15,1)}

con la condición de que s' H0L = -1; s' H15L = 2.

4. Escribe tu nombre o apellido usando interpolación con funciones splines cúbicos mediante un sólo trazo, con la instrucción

SplineFit[puntos, Cubic]

EJEMPLO :

10 20 30 40

5

10

15

20

25

30

Práctica 7 INTERPOLACIÓN 5.1. Interpolación Polinómicajomalapa/Practicas AYMN...

Documents

Transcript of Práctica 7 INTERPOLACIÓN 5.1. Interpolación Polinómicajomalapa/Practicas AYMN...