Universidad de La FronteraTEMUCO 02 Junio 2010

Margareth Sepulveda C. - Miguel Pichipillan S.

1 Volumen - Pappus

1.1 Centro de masa

Supongase que dos masas de tamano m1 y m2 se colocanen un sube y baja a distancias respectivas de d1 y d2del punto de apoyo (centro) y en lados opuestos a el(vease la figura 1). El sube y baja se equilibra solo sid1 ·m1 = d2 ·m2.

Un buen modelo matematico para esta situacion se obtienen al reem-plazar el sube y abnaja por une coordenado horizontal ue tenga su origen enel centro (vease la figura 2). Entonces la coordenada x (abscisa) de m1 esx1 = −d1, la de m2 es x2 = d2 y la condicion de equilibrio es.

x1m1 + x2m2

El producto de la masa m de una partıcula por su distancia dirigidadesde un punto (su brazo palanca) se denomina momento de la partıculapor respecto a ese punto (vease figura 3). Asimismo, mide la tendencia dela masa a producir una rotacion alrededor de ese punto. La condicion paraque dos masas a lo largo de esta recta esten en equilibrio es que la suma desus momentos con respecto al punto sea cero.

1

La situacion que se acaba de describir puede generalizarse. El momentototal M (con respecto al origen) de un sistema de n masas m1,m2...mn

ubicados en los puntos x1, x2, · · · , xn a lo largo del eje x es la suma de losmomentos individuales; es es.

M = x1m1 + x2m2 + · · ·+ xnmn =n∑

i=1

ximi

La condicion para el equilibrio en el origen es que M=0. Por supuesto, nodebemos esperar equilibrio en el origen, excepto en circuntancias especiales.Pero seguramente un sistema de masas se equilibrara en alguna parte. Lapregunta es donde. ¿Cual es la abscisa del pounto en donde el centro debecolocarse para que el sistema en la figura 4 este en equilibrio?

Llamese x a la coordenada deseada. El momento total con respecto aesta debe ser cero: esto es,

(x1 − x)m1 + (x2 − x)m2 + · · ·+ (xn − x)mn

o

x1m1 + x2m2 + · · ·+ xnmn = xm1 + xm2 + · · ·+ xmn

Cuando despejamos a x, obtenemos

x =M

m=

n∑

i=1

ximi

n∑

i=1

mi

El punto x es denominado centro de masa, es el punto de equilibrio.Observe que solo es el momento total con respecto al origen divido entre la

2

masa total.

1.1.1 Distribucion continua de masa a lo largo de una recta

Un segmento recto de un alambre delgado de densidadvariable (masa por unidad de longitud) para el que quer-emos encontrar el punto de equilibrio. Colocamos uneje coordenado a lo largo del alambre y seguimos nue-stro procedimiento usual de rebanar, aproximar e inte-grar. Suponiendo que la densidad en x es δ(x). Primeroobtenemos la masa total m y despues el momento totalM con respoecto al origen (vease figura 6). Esto lleva ala formula

∆m ≈ δ(x)∆x ∆M ≈ xδ(x)∆x

m =∫ b

aδ(x)dx M =

∫ b

axδ(x)dx

x =M

m=

∫ b

axδ(x)dx

∫ b

aδ(x)dx

1.1.2 Distribucion de masa en el plano

Considere n masas puntuales de magnitudes m1,m2, ...,mn situadas en lospuntos (x1, y1), (x2, y2), ..., (xn, yn) en el plano coordenado. Entonces, los mo-mentos totales Mx y My respecto al eje y y al eje x, respectivamente, estandados por

My =n∑

i=1

ximi Mx =n∑

i=1

yimi

Las coordenadas (x,y) del centro de masa (punto de equilibrio) son:

3

x =My

m=

n∑

i=1

ximi

n∑

i=1

mi

y =Mx

m=

n∑

i=1

yimi

n∑

i=1

mi

Considere la lamina homogenea acotada por x = a, x = b, y = f(x), yy = g(x), con g(x) ≤ f(x). Rebane esta lamina en delgadas tiras paralelasal eje y, las cuales por lo tanto tienen forma casi rectangular, e imagine lamasa de cada tira concentrada en su centro geometrico. Despues aproxime eintegre (vease figura 6). Con base en esto podemos calcular las coordenadas(x, y) del centro de masa utilizando las formulas

x =My

my =

Mx

m

∆m ≈ [f(x)− g(x)]∆x ∆My ≈ xδ[f(x)− g(x)]∆x ∆Mx ≈ δ2[(f(x))2 − (g(x))2]∆x

m = δ∫ b

a[f(x)− g(x)]dx My = δ

∫ b

ax[f(x)− g(x)]dx Mx = δ

2

∫ b

a[f2(x)− g2(x)]dx

Cuando lo hacemos, se cancela el factor δ del numerador y del denominador,y obtenemos

x =

∫ b

ax[f(x)− g(x)]dx

∫ b

a[f(x)− g(x)]dx

4

y =

∫ b

a

f(x) + g(x)

2[f(x)− g(x)]dx

∫ b

a[f(x)− g(x)]dx

=

1

2

∫ b

a[(f(x))2 − (g(x))2]dx

∫ b

a[f(x)− g(x)]dx

Algunas veces, rebanar en direccion paralela al eje x funciona mejor que re-banar en direccion paralela al eje y. Esto conduce a formulas para x y y enla que y es la variable de integracion.

El centro de masa de una lamina homogenea no depende de su masa o densidad, sino solo de la forma

de la region correspondiente en el plano. Ası que nuestro problema se convierte en un problema geometrico

en lugar de uno fısico. En consecuencia. frecuentemente hablamos de centroide de una region plana en

lugar del centro de masa de una lamina homogenea.

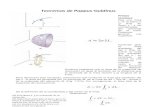
2 Teorema de Pappus

Si una region R, que esta de un lado de la recta en su plano, se hace giraralredor de esta recta, el volumen del solido resultante es igual al area de R

(A) multiplicada por la distancia recorrida por su centroide.

V = 2πAd

Sea la recta Ax+By + C y el punto (a, b) la distancia d =|Aa+Bb+ C|√

A2 +B2

5

2.1 Ejemplos

La region limitada por (x− 5)2 + y2 = 16 alrededor de:

1. Hallar el volumen del solido de revolucion generado al rotar:

(a) Eje y

(b) la recta x = −2

Alrededor del eje y :Primero calculemos el area a rotar, sabemos que es una circunferenciade radio 4 por lo tanto su area sera de 16π ahora obtenemos las coor-denadas del centroide

x = 5 y = 0

como la distancia de la recta de giro al centroide es de 5 aplicandoPappus obtenemos el volumen

Vy = 2π · 5 · 16π = 160π2u2

Alrededor de la recta x = −2como la distancia de la recta de giro al centroide es 7, aplicando Pappusobtenemos el volumen

Vy = 2π · 7 · 16π = 224π2u2

2. La region limitada por x2+(y−3)2 = 4 al rededor de la recta 2x−3y = 6

6