Nota Álgebra II- General

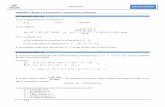
1 Notas de Eduardo Ortiz R. del curso de Álgebra II impartido por la Dra. Myriam Maldonado R.

Matrices no singulares

Definición: Sea 𝐴 ∈ 𝑀𝑛(𝐑) decimos que 𝐴 es no singular si existe 𝐵 ∈ 𝑀𝑛(𝐑) tal que

𝐴𝐵 = 𝐵𝐴 = 𝐼

Proposición: Si 𝐴, 𝐵 ∈ 𝑀𝑛(𝐑) son no singulares, entonces 𝐴𝐵 es no singular.

Observación: Sea 𝐴 ∈ 𝑀𝑛(𝐑). Si 𝐴 es no singular entonces existe una única

matriz 𝐵 ∈ 𝑀𝑛(𝐑) tal que 𝐴𝐵 = 𝐵𝐴 = 𝐼.

Notación: A la única matriz que satisface 𝐴𝐵 = 𝐵𝐴 = 𝐼 la denotaremos por

𝐴−1.

𝐴𝐴−1 = 𝐴−1𝐴 = 𝐼

Observación: Si 𝐴, 𝐵 ∈ 𝑀𝑛(𝐑) son no singlares entonces

(𝐴𝐵)−1 = 𝐵−1𝐴−1

Observación: Si 𝐴 ∈ 𝑀𝑛(𝐑) es no singular entonces 𝐴−1 es no singular, más

aun

(𝐴−1)−1 = 𝐴

Definición: Sea 𝐸 ∈ 𝑀𝑛(𝐑) decimos que 𝐸 es una matriz elemental si se

obtiene de 𝐼 a través de una única operación elemental.

Notación:

Si 𝑅 es la operación

𝑅𝑖 ↔ 𝑅𝑗

Entonces 𝐸 = 𝐸𝑖𝑗


𝑅𝑖 ↔ 𝑟𝑅𝑖

Entonces 𝐸 = 𝐸𝑖(𝑟)


𝑅𝑖 ↔ 𝑅𝑖 + 𝑟𝑅𝑗

Entonces 𝐸 = 𝐸𝑖𝑗(𝑟)


Proposición: Sean 𝐴, 𝐵 ∈ 𝑀𝑚𝑥𝑛(𝐑). Sea 𝑅 una operación elemental. Sea 𝐸 la

matriz elemental de oren m correspondiente a 𝑅. Si 𝐵 se obtiene de 𝐴 al

aplicar 𝑅, entonces:

𝐸𝐴 = 𝐵

Proposición: las matrices elementales son no singulares.

Teorema: Sea 𝐴 ∈ 𝑀𝑛(𝐑). Entonces las siguientes condiciones son

equivalentes:

I) 𝐴 es no singular.

II) 𝐴 ≡𝑅 𝐼

III) 𝐴𝑋 = 𝐵 tiene una única solución, ∀𝐵 ∈ 𝑀𝑚𝑥𝑛(𝐑).

IV) 𝐴𝑋 = 0 tiene una única solución.

V) 𝐴 es producto de matrices elementales.

VI)Existe 𝐶 ∈ 𝑀𝑛(𝐑) tal que 𝐶𝐴 = 𝐼

VII) 𝐴 ≡𝐶 𝐼

VIII) 𝑋𝐴 = 0 tiene única solución.

IX) 𝑋𝐴 = 𝐵 tiene única solución, ∀𝐵 ∈ 𝑀𝑚𝑥𝑛(𝐑).

X) 𝐴 es producto de matrices elementales por columnas.

XI) Existe 𝐵 ∈ 𝑀𝑛(𝐑) tal que

𝐴𝐵 = 𝐼

𝐴 → 𝐵𝐸𝑅 𝐴 → 𝐵𝐹

𝐶

𝐸𝐴 = 𝐵 𝐴𝐹 = 𝐵


Espacios vectoriales

Definición: Sea 𝑉 un conjunto no vacío. Decimos que 𝑉 es un espacio vectorial real si en 𝑉 se tienen dos operaciones

+: 𝑉𝑥𝑉 → 𝑉(𝛼, 𝛽) → 𝛼 + 𝛽

∙ ∶ 𝑹𝑥𝑉 → 𝑉(𝑎, 𝛼) → 𝑎𝛼

Las cuales satisfacen:

1) Si 𝛼, 𝛽, 𝛾 ∈ 𝑉, entonces (𝛼 + 𝛽) + 𝛾 = 𝛼 + (𝛽 + 𝛾)

2) Si 𝛼, 𝛽 ∈ 𝑉, entonces 𝛼 + 𝛽 = 𝛽 + 𝛼

3) Existe un único elemento en 𝑉 denotado por 𝑂𝑉 tal que 𝑂𝑉 + 𝛼 = 𝛼

4) Para cada elemento 𝛼 ∈ 𝑉 existe un único elemento en V denotado por – 𝛼 que satisface que

𝛼 + (−𝛼) = 𝑂𝑉 5) Si 𝛼, 𝛽 ∈ 𝑉 y 𝑎 ∈ 𝑹, entonces

𝑎(𝛼 + 𝛽) = 𝑎𝛼 + 𝑎𝛽 6) Si 𝑎, 𝑏 ∈ 𝑹 y 𝛼 ∈ 𝑉, entonces

(𝑎 + 𝑏)𝛼 = 𝑎𝛼 + 𝑏𝛼 7) Si 𝑎, 𝑏 ∈ 𝑹 y 𝛼 ∈ 𝑉, entonces

(𝑎𝑏)𝛼 = 𝑎(𝑏𝛼) = 𝑏(𝑎𝛼) 8) Si 𝛼 ∈ 𝑉, entonces

1 ∙ 𝛼 = 𝛼 (𝑉, +,∙)

Nota:

El elemento 𝑂𝑉 es llamado vector cero de 𝑉.

A los elementos de 𝑉 les llamaremos vectores.

A los elementos de 𝑹 los llamaremos escalares.


Proposición: Sea𝑉 un espacio vectorial real, entonces

1) 0 ∙ 𝛼 = 𝑂𝑉 , ∀𝛼 ∈ 𝑉 2) 𝑟𝑂𝑉 = 𝑂𝑉 , ∀𝑟 ∈ 𝑹 3) Si 𝛼, 𝛽, 𝛾 ∈ 𝑉, tales que 𝛼 + 𝛽 = 𝛽 + 𝛾, entonces 𝛼 = 𝛾 4) Si 𝑟 ∈ 𝑹 y 𝛼 ∈ 𝑉, entonces (−𝑟)𝛼 = 𝑟(−𝛼) = −(𝑟𝛼)

Si 𝑟 ∈ 𝑹 y 𝛼 ∈ 𝑉 tales que 𝑟𝛼

Subespacios Definición: Sea 𝑉 un espacio vectorial real. Sea 𝑊 ⊆ 𝑉, no vacío. Decimos que 𝑊 es un subespacio de 𝑉 si con las operaciones que hacen a 𝑉 un espacio vectorial 𝑊 también lo es.

Proposición: Sea 𝑉 un espacio vectorial real. Sea 𝑊 ⊆ 𝑉. Entonces 𝑊 es un subespacion de 𝑉 si y s

1) Si 𝑂𝑉 ∈ 𝑊 2) Si 𝛼, 𝛽 ∈ 𝑊, entonces 𝛼 + 𝛽 ∈ 𝑊 3) Si 𝑟 ∈ 𝑹 y 𝛼 ∈ 𝑉, entonces 𝑟𝛼 ∈ 𝑊

Proposición: Sea 𝑉 un espacio vectorial real. Si 𝑊1 y 𝑊2 son Subespacios de 𝑉, entonces 𝑊1 ∩ 𝑊2 es un subespacio de 𝑉

Observación: La unión de Subespacios no necesariamente es un subespacio.

Definición: Sea 𝑉 un espacio vectorial real. Sean 𝑊1, 𝑊2 ⊆ 𝑉. Definimos

𝑊1 + 𝑊2 = {𝛼 + 𝛽|𝛼 ∈ 𝑊1 𝑦 𝛽 ∈ 𝑊2}

Proposición: Sea 𝑉 un espacio vectorial real. Si 𝑊1 y 𝑊2 son Subespacios de 𝑉, entonces 𝑊1 + 𝑊2 es un subespacio de 𝑉

Conjuntos linealmente dependientes y conjuntos linealmente independientes

Definición: Sea 𝑉 un espacio vectorial real. Sean 𝛼1𝛼2, … , 𝛼𝑛 ∈ 𝑉 . Una combinación líneas de 𝛼1𝛼2, … , 𝛼𝑛 es una expresión de la forma

𝑎1𝛼1 + 𝑎2𝛼2 + ⋯ + 𝑎𝑛𝛼𝑛

Donde 𝑎𝑖 ∈ 𝑹, ∀𝑖 = 1,2, … , 𝑛


Definición: Sea 𝑉 un espacio vectorial real. Sean 𝛼1𝛼2, … , 𝛼𝑛 ∈ 𝑉. Decimos que {𝛼1𝛼2, … , 𝛼𝑛} es un conjunto linealmente independiente (𝑙. 𝑖. ) si 𝑎1𝛼1 + 𝑎2𝛼2 + ⋯ + 𝑎𝑛𝛼𝑛=0, entonces 𝑎𝑖 = 0, ∀𝑖 = 1,2, … , 𝑛 En caso contrario diremos que {𝛼1𝛼2, … , 𝛼𝑛} es un conjunto linealmente dependiente (𝑙. 𝑑. ).

Definición: Sea 𝑉 un espacio vectorial real. Sea 𝑆 ⊆ 𝑉. Decimos que 𝑆 es 𝑙. 𝑖. si todo subconjunto de 𝑆 finito es linealmente independiente. En caso contrario diremos que 𝑆 es 𝑙. 𝑑.

Observación: Sea 𝑉 un espacio vectorial real. Sea 𝑆 ⊆ 𝑉 𝑙. 𝑖. Si 𝐴 ⊆ 𝑉, entonces 𝐴 es 𝑙. 𝑖.

Observación: Sea 𝑉 un espacio vectorial real. Sea 𝑆 ⊆ 𝑉 𝑙. 𝑖. Si 𝛼 ∈ 𝑉, entonces 𝑆 ∪ {𝛼} no necesariamente es 𝑙. 𝑖.

Proposición: Sea 𝑉 un espacio vectorial real. Sean 𝛼1𝛼2, … , 𝛼𝑛 ∈ 𝑉 entonces {𝛼1𝛼2, … , 𝛼𝑛} es 𝑙. 𝑑. si y sólo si existe 𝑖 ∈ {1,2, … 𝑛} tal que

𝛼𝑖 = 𝑎1𝛼1 + 𝑎2𝛼2 + ⋯ + 𝑎𝑖−1𝛼𝑖−1

= 𝑎1𝛼1 + 𝑎2𝛼2 + ⋯ + 𝑎𝑛𝛼𝑛

Proposición: Las filas no nulas de una matriz en forma escalonada forman un conjunto 𝑙. 𝑖.

Definición: Sea 𝑉 un espacio vectorial real y sea 𝑆 ⊆ 𝑉. Definimos el conjunto generado por 𝑆, denotado por 𝐿(𝑆) como

𝐿(𝑆) = {𝑎1𝛼1 + 𝑎2𝛼2 + ⋯ + 𝑎𝑛𝛼𝑛|𝑎𝑖 ∈ 𝑹, 𝛼1𝛼2, … , 𝛼𝑛 ∈ 𝑉 𝑦 𝑛 ∈ 𝑵 }

Proposición: Sea 𝑉 un espacio vectorial real. Si 𝑆 ⊆ 𝑉, con 𝑆 ≠ ∅, entonces:

1) 𝐿(𝑆) es un subespacio. 2) 𝑆 ⊆ 𝐿(𝑆) 3) Si 𝑊 es un subespacio de V tal que 𝑆 ⊆ 𝑊, entonces 𝐿(𝑆) ⊆ 𝑊.

Observación: 𝐿(𝑆) es el mínimo subespacio de V que contiene a S.

Observación: Sea 𝑉 un espacio vectorial real. Si 𝑊 es un subespacio de V. entonces 𝐿(𝑊) = 𝑊


Nota: Sea 𝑉 un espacio vectorial real. Sea 𝑆 ⊆ 𝑉, con 𝑆 ≠ ∅.

Sea 𝑊 = 𝐿(𝑆). En este caso decimos que 𝑆 genera a 𝑊.

Si {𝛼1𝛼2, … , 𝛼𝑛} ⊆ 𝑉, entonces en lugar de escribir 𝐿({𝛼1𝛼2, … , 𝛼𝑛}) escribiremos 𝐿(𝛼1𝛼2, … , 𝛼𝑛)

Definición: 𝐿(∅) = {𝑂𝑉}

Observación: ∅ es 𝑙. 𝑖.

Observación: Sea 𝑉 un espacio vectorial real. Sea 𝑆 ⊆ 𝑉 tal que 𝐿(𝑆) = 𝑉

Si 𝛼 ∈ 𝑉, entonces 𝐿(𝑆 ∪ {𝛼}) = 𝑉

Si 𝛽 ∈ 𝑉, entonces 𝐿(𝑆\{𝛽}) no necesariamente es 𝑉

Bases y dimensión

Definición: Sea 𝑉 un espacio vectorial real. Sea 𝐵 ⊆ 𝑉 no vacío. Decimos que 𝐵 es base de V si:

1) 𝐵 es 𝑙. 𝑖. 2) 𝐿(𝐵) = 𝑉

Proposición: Sea 𝑉 un espacio vectorial real. Sea 𝐵 ⊆ 𝑉. Entonces 𝐵 es base de 𝑉 si y sólo si todo elemento de 𝑉 se puede expresar de forma única como combinación lineal de elementos de 𝐵.

Proposición: Sea 𝑉 un espacio vectorial real. Sean {𝛼1𝛼2, … , 𝛼𝑛} ⊆ 𝑉 tal que 𝐿(𝛼1𝛼2, … , 𝛼𝑛) = 𝑉. Sea {𝛽1𝛽2, … , 𝛽𝑚} ⊆ 𝑉 𝑙. 𝑖. Entonces 𝑚 ≤ 𝑛.

Proposición: Sea 𝑉 un espacio vectorial real. Sean {𝛼1𝛼2, … , 𝛼𝑛} base de 𝑉 Si B es base de 𝑉, entonces |𝐵| = 𝑛

Definición: Sea 𝑉 un espacio vectorial real. Sea B una base de 𝑉. Si B es un conjunto finito de 𝑛 elementos, entonces diremos que 𝑉 es de dimensión finita 𝑛 y escribiremos

𝑑𝑖𝑚𝑉 = 𝑛 o 𝑑𝑖𝑚𝑹𝑉 = 𝑛

En caso contrario, es decir B un conjunto infinito, diremos que 𝑉 es de dimensión infinita.


Teorema: Sea 𝑉 un espacio vectorial de dimensión finita 𝑛, entonces:

1) Todo conjunto con más de 𝑛 vectores es 𝑙. 𝑑. 2) Ningún conjunto con menos de 𝑛 vectores genera a 𝑉.

Teorema: Todas las bases de un espacio vectorial de dimensión finita tienen el mismo número de vectores.

Proposición: Sea 𝑉 un espacio vectorial de dimensión finita 𝑛. A todo conjunto generador de 𝑉 se le puede extraer una base de 𝑉.

Proposición: Sea 𝑉 un espacio vectorial de dimensión finita 𝑛. Sea 𝑎 ={𝛼1𝛼2, … , 𝛼𝑛} ⊆ 𝑉 𝑙. 𝑖. Entonces 𝑎 se puede extender a una base de 𝑉

Proposición: Sea 𝑉 un espacio vectorial real de dimensión finita 𝑛. Sea 𝑊 un subespacio de 𝑉. Entonces

𝑑𝑖𝑚𝑊 ≤ 𝑛

Además si 𝑑𝑖𝑚𝑊 = 𝑛, entonces 𝑊 = 𝑉.

Teorema: Sea 𝑉 un espacio vectorial real de dimensión finita 𝑛. Sean 𝑊 y 𝑈 dos Subespacios de 𝑉. Entonces

𝑑𝑖𝑚(𝑊 + 𝑈) = 𝑑𝑖𝑚𝑊 + 𝑑𝑖𝑚𝑈 − 𝑑𝑖𝑚(𝑊 ∩ 𝑈)

Definición: Sea 𝑉 un espacio vectorial. Sean 𝑊 y 𝑈 dos Subespacios de 𝑉. Decimos que 𝑊 y 𝑈 forman una suma directa de 𝑉 si 𝑊 ∩ 𝑈 = {𝑂𝑉}. En tal caso escribiremos 𝑊 ⊕ 𝑈.

Espacio fila, espacio columna y espacio nulo de una matriz Definición: Sea 𝐴 ∈ 𝑀𝑚×𝑛(𝐑), definimos el espacio fila de 𝐴, denotado por 𝐹𝐴, como:

𝐹𝐴 = 𝐿(𝑅𝑜𝑤1(𝐴), 𝑅𝑜𝑤2(𝐴), … , 𝑅𝑜𝑤𝑚(𝐴))

Observación: Sea 𝐴 ∈ 𝑀𝑚×𝑛(𝐑), entonces 𝐹𝐴 es un subespacio de 𝑹𝒏.

Definición: Sea 𝐴 ∈ 𝑀𝑚×𝑛(𝐑). Definimos el espacio columna de 𝐴, denotado

por𝐶𝐴, como:

𝐶𝐴 = {𝐶𝑜𝑙1(𝐴), 𝐶𝑜𝑙2(𝐴), … , 𝐶𝑜𝑙𝑛(𝐴)}


Observación: Si 𝐴 ∈ 𝑀𝑚×𝑛(𝐑), entonces𝐶𝐴 es un subespacio de 𝑹𝒏.

Definición: Sea 𝐴 ∈ 𝑀𝑚×𝑛(𝐑). Definimos el espacio nulo de 𝐴, denotado por

𝑁𝐴, como:

𝑁𝐴 = {𝑥 ∈ 𝑹𝒏|𝐴𝑋 = 0}

Proposición: 𝑁𝐴 es un subespacio de 𝑹𝒏.

Definición: Sea 𝐴 ∈ 𝑀𝑚×𝑛(𝐑).

1) A la dimensión de 𝐹𝐴 le llamaremos rango fila de 𝐴.

2) A la dimensión de 𝐶𝐴 le llamaremos rango columna de 𝐴.

3) A la dimensión de 𝑁𝐴 le llamaremos la nulidad de 𝐴.

Proposición: Sean 𝐴 ∈ 𝑀𝑚×𝑛(𝐑) y 𝑥 ∈ 𝑹𝒏. Entonces 𝑥 ∈ 𝐶𝐴 si y sólo si el

sistema 𝐴𝑋 = 𝑌 tiene solución.

Proposición: Matrices equivalentes por renglones tienen el mismo espacio

fila.

Proposición: Sean 𝐴, 𝐵 ∈ 𝑀𝑚×𝑛(𝐑) en forma escalonada. Si 𝐹𝐴 = 𝐹𝐵,

entonces los unos principales de 𝐴 y 𝐵 están en las mismas posiciones.

Proposición: Dos matrices en forma escalonada reducida tienen el mismo

espacio fila si y sólo si tienen las mismas filas no nulas.

Proposición: Toda matriz es equivalente a una única matriz en forma

escalonada reducida.

Proposición: El rango fila y el rango columna de una matriz son iguales.

Definición: Sea 𝐴 ∈ 𝑀𝑚×𝑛(𝐑). Definimos por 𝑟𝑎𝑛𝑘(𝐴) como

𝑟𝑎𝑛𝑘(𝐴) = 𝑑𝑖𝑚𝐹𝐴 = 𝑑𝑖𝑚𝐶𝐴

Proposición: Si 𝐴 ∈ 𝑀𝑚×𝑛(𝐑), entonces

𝑟𝑎𝑛𝑘(𝐴) + 𝑑𝑖𝑚𝑁𝐴 = 𝑛

Nota Álgebra II- General

Documents

Transcript of Nota Álgebra II- General