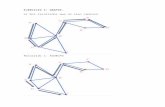
Ejercicios propuestos de grafos y digrafos
Click here to load reader
Transcript of Ejercicios propuestos de grafos y digrafos

UNIVERSIDAD FERMIN TORO
DECANATO DE INGENIERIA
CABUDARE EDO. LARA
Ejercicios propuestos
Grafos y Dígrafos.
EglisPargas
C.I 12.935.264
SAIA A
Prof. Adriana Barreta
Cabudare – Noviembre 2011

DADO EL SIGUIENTE GRAFO, ENCONTRAR:
a) Matriz de Adyacencia, se define como la matriz cuadrada nxn denotada por Ma (g)
cuya componente i, j es la multiplicidad m ( Vi, Vj) del par de vértices (Vi, Vj).
Ma (g) =
b) Matriz de Incidencia.Es aquella denotada por Mi (g) cuyo componente i, j es el número
de veces que la arista (a i) incide es el número de vértice (v j)
Mi (g) =
0 1 1 1 0 0 1 1 1 0 1 0 1 1 0 1 1 1 0 1 1 1 1 0 1 0 1 0 1 0 1 0 0 1 1 1 0 1 1 1 0 1 1 0 1 0 0 1 1 0 1 1 1 0 0 1 1 1 0 0 1 1 1 0
1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 1 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 1 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1

c) Es conexo?Justifique su respuesta.
Si es conexo, ya que todos los vértices se encuentran conectados por aristas,
cumpliendo así la definición que dice que un grafo será conexo si solo si se cumple que
para todo par de vértices u, V se tiene que U,V están conectados.
d) Es simple? Justifique su respuesta.
Si es simple, ya que no contiene lazos en ninguno de sus vértices.
e) Es regular? Justifique su respuesta.
No es regular, ya que no todos sus vértices tienen los mismos grados, en este caso:
V4 y V6 tienen grado 4.
V1,V2,V7 y V8 tiene grado 5.
V3 y V5 tienen grado 6.
f) Es completo? Justifique su respuesta.
Noes completo, ya que existen vértices que no le llegan aristas cumpliéndose así su
definición.
g) Una cadena simple no elemental de grado 6.
C = V7,A15,V4,A11,V3,A7,V6,A16,V5,A19,V8,A18,V7
h) Un ciclo no simple de grado 5.
C = V2,A10,V6,A20,V8,A19,V5,A16,V6,A10,V2
i) Árbol Generador aplicando el algoritmo constructor.
Paso 1: seleccionamos el vértice V1 entonces H1 = V1
Paso 2: seleccionamos la arista A1 entonces H2= V1, V2
V1
V1 A1
V2

Paso 3: seleccionamos la arista A3 entonces H3= V1, V2, V3
Paso 4: seleccionamos la arista A11 entonces H4= V1, V2, V3, V4
Paso 5: seleccionamos la arista A14 entonces H5= V1, V2, V3, V4, V5
Paso 6: seleccionamos la arista A16 entonces H6= V1, V2, V3, V4, V5, V6
V1 A1
V2
V3
A3
V1 A1
V2
V3
A3
V4
A11
V1 A1
V2
V3
A3
V4
A11
V5
A14
V1 A1
V2
V3
A3
V4
A11
V5
A14 A16
V6

Paso 7: seleccionamos la arista A20 entonces H7= V1, V2, V3, V4, V5, V6, V8
Paso 7: seleccionamos la arista A20 entonces H7= V1, V2, V3, V4, V5, V6, V8, V7
V1 A1
V2
V3
A3
V4
A11
V5
A14 A16
V6
V8
A20
V1 A1
V2
V3
A3
V4
A11
V5
A14 A16
V6
V8
A20
A18
V7

j) Subgrafo parcial.
k) Demostrando si es euleriano aplicando el algoritmo de Fleury.
Aplicando el algoritmo de Fleury se puede visualizar que el grafo no es Eureliano ya que es imposible que no se repitan las aristas en el recorrido.
l) Demostrar es Hamiltoniano
C= V1, A1,V2,A3,V3,A11,V4,A14,V5,A16,V6,A20,V8,A18,V7,A5V1
V1
V3
A2
A12
V7
A12
V2
V5
V6
V8
V1
A1
V2
V3
A3
V4
A11
V5
A14 A16
V6
V8
A20
A18
V7
A5

DADO EL SIGUIENTE DIGRAFO.
A) Encontrar matriz de conexión.
Mc =
B) Es simple? Justifique su respuesta.
Si es simple, ya que no existen ni lazos ni arcos paralelos entre las vértices,
cumpliéndose así su definición.
C) Encontrar una cadena no simple no elemental de grado 5.
C = V2, A2, V3, A7, V5, A10, V2, A2, V3, A8, V4
D) Encontrar un ciclo simple.
C = V2, A3, V4, A12, V6, A14, V5, A10, V2
0 1 1 0 1 0 0 0 1 1 1 0 0 0 0 1 1 0 1 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 1 0

E) Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad.
Mc1 =
Mc2=
Mc3=
Mc4=
Mc5=
Acc(D)= bin
0 1 1 0 1 0 0 0 1 1 1 0 0 0 0 1 1 0 1 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 1 0
0 0 1 1 1 1 1 0 0 1 1 1 1 1 0 1 0 1 0 1 1 0 1 0 1 0 1 1 1 1 0 1 0 0 1 1
0 1 1 0 1 0 0 0 1 1 1 0 0 0 0 1 1 0 1 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 1 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1 0 1
1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1
3 4 5 4 5 4 4 2 5 5 5 5 3 4 3 4 4 4 4 4 3 5 4 4 3 4 4 5 4 5 3 3 3 4 1 4

Un dígrafo finito D es fuertemente conexo la matriz Acc(D) no tienecomponentes
nulas.Por lo tanto se puede concluir que el grafo es fuertemente conexo.
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1