APLICACIÓN DE MÉTODOS ESTADÍSTICOS PARA LA PARA REGIONALIZACIÓN DE PRECIPITACIÓN MENSUAL EN EL VALLE DEL CAUCA

Yesid Carvajal Escobar1 Juan B. Marco Segura2

RESUMEN

A partir de la información histórica de 49 estaciones de medición de lluvias, ubicadas en el Valle geográfico del río Cauca, y tomando un período común de registros entre 1972-1998, se realizó una clasificación de las estaciones, aplicando el método de cluster jerarquizado. Se conformaron tres grupos homogéneos para la región. Los resultados se comprobaron aplicando los métodos estadísticos de Dalrymple (1960) Wiltshire y Berán (1987b) y Análisis Discriminante de las Componentes Principales (CP), tomando las 10 primeras componentes (Jhonson, 2000). Igualmente, se verificó la coherencia geográfica de los grupos obtenidos. Se hace un análisis comparativo de las ventajas y desventajas de los diferentes métodos de regionalización, así como de los beneficios de agrupar la información hidrometeorológica cuando se hace un tratamiento conjunto de los datos. Aunque la mejor alternativa es el método geográfico, este debe ser comprobado mediante un test estadístico que valide los resultados de la agrupación.

Palabras clave: Homogeneización de series de precipitación y caudal, regionalización, Análisis estadístico, Análisis de consistencia de la información hidrometeorológica

ABSTRACT

Starting from the historical information of 49 rain gauge stations, located in the geographical Valley of the river Cauca, a classification of the stations was carried out applying the method of nested cluster. The precipitation data has been measured during a period 1972-1998. The three homogeneous groups for the mentioned region has been conformed. The results were proven applying the statistical methods of Dalrymple (1960), Wiltshire and Berán (1987b) and Discriminant Analysis of the Principal Components (CP), using the first 10 components (Jhonson, 2000). Also the geographical coherence of the obtained groups was verified. A comparative analysis of the advantages and disadvantages of the different regionalization methods has been sorted out, as well as of the benefits of the hydrometeorological information in the case of a combined treatment of the data. Although the best alternative is the geographical method, this it should be proven by means of a statistical test that validates the results of the grouping.

Palabras clave: Homogeneización de series de precipitación y caudal, regionalización, Análisis estadístico, Análisis de consistencia de la información hidrometeorológica.

1. ANTECEDENTES

1Profesor Asociado Universidad del Valle Cali-Colombia. Candidato a Doctorado en Hidráulica y Medio Ambiente. Universidad Politécncia de Valencia. Email: yecarvaj@hma.upv.es

2 Profesor Catedrático. Universidad Politécnica de Valencia- España

1

1.1 METODOS DE REGIONALIZACION

La mayor parte de los métodos de regionalización desarrollados se efectúa para el análisis estadístico de frecuencias de máximos de una variable hidrológica. La estimación de parámetros a partir de una muestra de reducido tamaño muchas veces presenta dificultades, debido a la incertidumbre existente respecto a su representatividad. Incluso, cuando se asume una única población, el coeficiente de variación (Cv) y el de asimetría (Cs) calculado en distintas muestras presenta una elevada dispersión de los parámetros y cuantiles estimados. Esta varianza es mayor cuanto más reducida es la muestra y más alto el valor del Cv. Lo anterior conduce a métodos que asumen una región homogénea respecto a ciertas características estadísticas, lo que permite aprovechar el conjunto de información disponible en la región. La fase más importante en la utilización de información regional, es la de definir las estaciones de precipitación o caudal que se consideran similares entre sí, y que puedan ser agrupadas según el grado de heterogeneidad que se quiera asumir para tener un beneficio en el tratamiento conjunto de la información. Aunque no existe un procedimiento que asegure correctamente la definición de una región para el análisis de precipitación o caudal, Lettenmaier y Potter (1985), reportan las ventajas de agrupar los datos de precipitación máxima de distintas estaciones con Cv bajos (Cv

medio < 0.6) y homogéneos (Cv (Cv) < 0.2). En el análisis de precipitación máxima, dada la variabilidad muestral del Cs y Cv, la mayoría de los métodos toma como base su regionalización. Ferrer (1996) menciona las siguientes hipótesis de homogeneidad en su respectivo orden: El Cs constante en la región, el Cs constante en la región y el Cv constante en cada subregión, El Cs y el Cv constante en la región. Es muy poca la referencia que se hace de regionalización para otro tipo de análisis. En este caso, se planteó para regionalizar la serie completa de los registros de lluvia mensual, para el tratamiento conjunto de los datos.

El objetivo de los métodos estadísticos regionales es permitir establecer regiones homogéneas para la estimación de caudal o lluvia en puntos sin medición, así como permitir un tratamiento más robusto con el conjunto de estaciones que se consideren homogéneas. Estos métodos requieren tres fases en su aplicación: Identificar la región, establecer características conocidas de las estaciones (coordenadas, altitud, edafología, climatología, etc) y los parámetros o estadísticos a estimar. Ferrer (1996) cita que estas condiciones definen tres tipos de métodos para la delimitación de regiones: el geográfico, el estadístico y el de regiones de características específicas.

El método geográfico consiste en agrupar las estaciones en función de sus coordenadas, frecuentemente, coincidiendo con divisiones administrativas. Tiene la ventaja de permitir asignar un punto sin registro pluviométrico o una cuenca sin datos de caudal. Sin embargo, puede plantear problemas con la homogeneidad de la región. Debido a la relativa continuidad espacial de las lluvias, es más coherente definir regiones geográficas en un análisis de lluvias que en uno de caudal, porque en éste último, las cuencas vecinas, pueden presentar entre otras, características edafológicas, geológicas, o de cobertura vegetal diferentes. El método estadístico permite clasificar las estaciones según su comportamiento estadístico, para definir los grupos homogéneos. A diferencia del anterior, emplea algoritmos automáticos de análisis discriminante, factorial o de cluster. La bibliografía reporta varios casos de aplicación: De Coursey (1973) en EU clasificó 90 estaciones de caudal, en tres grupos, aplicando análisis discriminante, basándose en tres estimaciones empíricas de 4 cuantiles de crecientes. Mosley (1981) empleó el cluster jerarquizado en Nueva Zelanda para agrupar estaciones de caudal teniendo en cuenta la proximidad en un espacio bidimensional conformado por el Cv y el caudal medio específico (m3/Km2) de

2

los registros de caudal máximo. Recientemente, ARIDE (2001) aplicó el mismo método para clasificar 5244 estaciones de caudal, en grupos con un patrón climático común, utilizando el coeficiente de correlación de Pearson como medida de similaridad.

Los algoritmos de cluster jerarquizado agrupan estaciones progresivamente, clasificándolas en diferentes grupos, hasta minimizar la suma total del cuadrado de las distancias de cada una al centroide de cada grupo en diferentes etapas. Esto conduce normalmente, a una o dos regiones importantes con pequeños grupos en la periferia. Así lo mencionan Mosley (1981) y Acreman y Sinclair (1986). Es de los métodos más empleados, Wiltshire (1986) y Wiltshire y Beran (1987ª) lo emplearon para agrupar 376 estaciones de caudal en Gran Bretaña. E Instituto del Agua (1992) analizado, lluvias máximas diarias, empleando cluster no jerarquizado como primera aproximación en la determinación de las regiones. Una desventaja del método es la definición arbitraria del número de regiones a obtener, por la falta de fronteras claras. Esto se resuelve tratando de obtener regiones homogéneas aplicando test estadísticos u obteniendo una representación geográfica coherente de las mismas. ARIDE (2001) considera que la selección del número final de grupos, puede hacerse graficando el coeficiente de correlación promedio de cada grupo versus el número de clusters. Teóricamente, un paso con un significativo cambio en el coeficiente de correlación de los grupos conformados, permite definir el número de grupos. El método ofrece mejores resultados en lluvias. Mosley (1981) obtuvo una coherencia espacial de la agrupación estadística en la zona sur de Nueva Zelanda, con gran dispersión espacial de los resultados en la zona norte. Otra desventaja, es la dificultad para asignar un punto sin registros de determinada región en un conjunto de regiones previamente definidas porque no se conocen los valores estadísticos empleados como discriminantes en la clasificación. Esto se resuelve en el caso de lluvias, si la clasificación estadística tiene una adecuada correspondencia geográfica, mientras que en el caso de caudal, se resuelve si se encuentran relaciones entre las características estadísticas discriminantes y determinadas características específicas de las cuencas: fisiográficas, meteorológicas, etc. Otro inconveniente es que emplea estadísticos muestrales que tienen asociados una elevada varianza. En este sentido, las agrupaciones realizadas pueden amplificar artificialmente unas diferencias entre regiones que en gran parte pueden deberse a un simple efecto aleatorio. Esta dificultad se abordó en el estudio, realizando preliminarmente un ACP para disminuir dicho ruido.

El método de características específicas, es muy empleado en análisis de caudal y menos en lluvia, dada la necesidad de estimar caudal en cuencas sin aforo cuando sólo se dispone de las características fisiográficas, edafológicas y meteorológicas. Asumiendo grupos previos con criterios estadísticos, el análisis discriminante asume que las m características específicas seleccionadas siguen una distribución normal adimensional y que su matriz de covarianzas es común para todos. Bajo estas hipótesis se aplica el teorema de Bayes para obtener la probabilidad de que una estación con unas características específicas dadas pertenezca a un grupo preexistente, asignando finalmente la estación al punto con mayor probabilidad de pertenencia. En este método se emplean unas características específicas que luego clasifican aplicando análisis factorial, cluster o discriminante.

El análisis discriminante permite clasificar estaciones en función de determinadas características específicas y cuantificar la probabilidad de que una de ellas pertenezca a uno de los grupos previamente formados con otros criterios. La clasificación en función de características específicas difícilmente se confirma al comparar los estadísticos observados, por lo que es preferible utilizar características estadísticas.

3

Wiltshire (1987ª) aplicó Análisis discriminante para clasificar una cuenca, conociendo 9 de sus características específicas, en uno de los 10 grupos previamente definidos estadísticamente. La comprobación realizada en 376 estaciones de caudal dió clasificaciones muy diferentes. Resultados similares reporta FREND (1989) al aplicar el método en cuencas de Europa asumiendo 10 grupos ya existentes y 7 características específicas. Esto indica la dificultad para relacionar estadísticos de caudal y características específicas de las cuencas.

1.2 EXPERIENCIAS DE REGIONALIZACION EN EL VALLE DEL CAUCA

Regalado et al (1984), realizaron el “Estudio regional de frecuencias de caudales máximos para las cuencas del Pacífico”, usaron para el análisis probabilístico de las series hidrológicas, las distribuciones de Log-Pearson tipo III, Gumbel y Log–Normal. Calcularon mediante regresiones múltiples el caudal máximo en función del área, longitud del cauce principal y pendiente media. Determinaron también la relación entre el caudal máximo promedio diario y el caudal máximo instantáneo, bajo un factor constante de 1.3, recomendando usar el valor más crítico.

En Mejía y Perry (1987) desarrollaron el Estudio de Aguas en el área geográfica del Valle el Cauca, donde se presentan los trabajos orientados al desarrollo de modelos de planeamiento para lograr un mejor aprovechamiento del recurso hídrico para todo tipo de usos en la región. El estudio hidrológico estuvo orientado a la regionalización de los parámetros hidrológicos básicos que controlan el comportamiento de las series de tiempo de los caudales de los diferentes tributarios en la zona geográfica del Valle del Cauca. Se regionalizó el caudal medio multianual identificando seis zonas dentro del Valle del Cauca que presentan comportamiento similar en cuanto a las características estacionales de los caudales mensuales.

Erazo (1.998), regionalizó caudales máximos de diseño en las cuencas del departamento de Valle del Cauca, delimitando regiones hidrológicamente homogéneas con información geomorfología, geológica, de suelos, vegetación y precipitación. Las regiones fueron evaluadas con dos pruebas estadísticas la de Gumbel y la de Wiltshire.

Arias y Soto (2000), regionalizaron caudales medios de las corrientes superficiales afluentes del río Cauca en los departamentos del Cauca y Valle del Cauca, por medio del método de regionalización de características medias, calculando el caudal medio asociado a diferentes periodos de retorno. Similar trabajo reporta Escobar (2001) para caudales mínimos en dicha región.

2. METODOLOGIA2.1 SELECCIÓN DE LA INFORMACIÓN Y ANÁLISIS PREVIO DE CONSISTENCIA

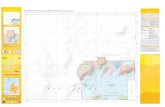
Se recopiló la información de precipitación, proveniente de CVC Corporación Autónoma Regional del Valle del Cauca, preseleccionando 96 estaciones de lluvia, ubicadas en el Valle geográfico. Seguidamente, mediante criterios de selección tales como: cobertura, tiempo de registro (estaciones con 15 o más años de registro), cantidad de datos faltantes y calidad de la información, se escogieron 49 estaciones pluviométricas, buscando series confiables con un período común de registros (1972-1998). La figura 1 presenta la localización de las estaciones. Los datos faltantes se

4

calcularon aplicando regresión multivariada con los datos de las estaciones más cercanas. Luego, se efectuó el análisis exploratorio, analizando gráficos de tiempo, de masa simple, de doble masa, residual, Q-Q y P-P. Posteriormente, se efectuó el análisis confirmatorio aplicando pruebas estadísticas de homogeneidad de medias y varianza: para la media: prueba T con y sin cambio de varianza, prueba F, prueba de Mann-Whitney, prueba z de Kolmogorov-Smirnov, prueba de Friedman, prueba de Kendall, prueba del signo, prueba de Wilcoxón de los rangos con signo, prueba de Kruskal Wallis. prueba de la mediana, para la estimación de tendencias, prueba T para detección de pruebas lineales. Para detectar cambio de varianza: prueba de de Levene. Mesa et al (1998).

De las 49 estaciones consideradas, el 90% no tienen tendencia significativa, el 10 % muestran tendencia lineal, y El 10% presentaron cambio significativo en la varianza, corrigiéndose dichas tendencias. La conclusión general es que esta variable no muestra evidencia de cambio climático, coincidiendo con resultados reportados por Mesa et al (1998) en Colombia.

2.2 METODOS ESTADÍSTICOS DE REGIONALIZACION DE LAS SERIES DE PRECIPITACION

2.2.1 Análisis de cluster jerarquizado. Previa estandarización de las series de datos de precipitación de las estaciones, se efectuó un análisis de cluster jerarquico. Hay diferentes criterios para calcular distancias entre datos y variables, así como para combinarlos en los clusters. El más habitual y utilizado es el análisis cluster jerárquico aglomerativo. En éste, los clusters son formados agrupando en clusters cada vez más grandes hasta que todos forman parte de uno único. Como medida de similaridad, se empleó el promedio entre grupos del coeficiente de correlación, y se definió la distancia entre dos clusters como la media de los coeficientes de correlación entre todas las combinaciones posibles dos a dos de los datos de uno y otro cluster. El procedimiento se repitió, conformando grupos desde n = 1 hasta 49 estaciones, a partir de la matriz 49 x 324 meses (27 años). Se determinó el número de grupos homogéneos graficando los grupos conformados versus el coeficiente de correlación promedio de Pearson entre los grupos establecidos. (ver figura 2), obteniendo el número de grupos en el punto donde ocurre un cambio significativo de la misma. (3 grupos homogéneos). ARIDE (2001).

2.2.2 Métodos estadísticos de comprobación. Como métodos estadísticos de comprobación, para verificar la clasificación de los grupos homogéneos, se emplearon los métodos de Dalrymple (1960), Wiltshire y Berán (1987b) y el Análisis Discriminante a las 10 primeras componentes principales de los datos de precipitación. Así mismo, se verificó la consistencia geográfica de la agrupación estadística realizada, confirmando una distribución espacial coherente de las estaciones de cada grupo.

Método de Dalrymple (1960). Analiza la variabilidad de las estimaciones del cuartil De Tr=10 años, asumiendo una función de distribución EV1 para la serie de máximas precipitaciones mensuales, y una distribución normal de las estimaciones de los cuantiles, para determinar la región de confianza del 95% para el cuantil de 10 años, en función de la longitud de la serie. Los límites de confianza son expresados en años y comparados con el Tr asociado al cuantil regional de 10 años resultante de un ajuste local gráfico a los datos de cada estación. Una estación cuyo Tr asociado no está incluido en los límites de confianza, es excluida de la región.

5

Método de Wiltshire y Berán (1987b). Aplicaron un método, empleando un estadístico R que mide la variación en la región del valor G´, definido para cada estación j con una serie de nj años, con la siguiente expresión:

Siendo Gij = F(Xij), es decir el valor de la función de probabilidad asociada al valor Xij, resultante del ajuste regional de la distribución F(x) a los datos de la estación j. Si la región es homogénea, los valores de Gij se distribuirán según una distribución uniforme (0,1) y el valor teórico de G j será de 0.5. Las variaciones de G j dentro de la región son cuantificadas con el estadístico R que se distribuye según una con n-1 grados de libertad, siendo n el número de estaciones que componen la región. Si el valor de R excede (1-), se rechaza la hipótesis de homogeneidad. Mediante simulaciones de Montecarlo, Wiltshire muestra que R se distribuye según una pero la potencia estadística del test es moderada. Otra desventaja es la necesidad de estimar previamente la ley regional F(x) para calcular G ij y tiene como ventaja la posibilidad de aplicación a cualquier tipo de regionalización.

Definición: Sea una muestra aleatoria (x1, x2,….xn) procedente de una determinada población con una función de distribución F(x). A cada uno de dichos valores se le puede asociar un Gj definido según:

Gj = F(Xi)

G1,G2, …,Gn deben tener, a parte de las desviaciones causadas por los efectos de la variabilidad muestral, una distribución de frecuencia uniforme (0,1). Si la muestra corresponde a las series máximas anuales, es necesario dividirlas previamente por el valor medio de la serie para hacerlas adimensionales. Los puntos G deberán presentar una distribución uniforme lo que constituye la base del test de homogeneidad. El parámetro seleccionado por Wiltshire y Berán (1987b) para cuantificar la aproximación de los puntos G en una serie j a la distribución uniforme es:

Siendo Gij el valor del punto G para el elemento i de la muestra j constituida por nj

elementos. El anterior parámetro debería G´j debe aproximarse a la media de la distribución uniforme: 0.5 y por la transformación planteada ser capaz de discriminar muestras con Cv de la población supuesta al amplificar las diferencias. La homogeneidad regional es finalmente caracterizada mediante la variabilidad de R de los distintos Gj´ en las N estaciones, definida según:

Donde G’ es el valor medio regional de los Gj’ obtenido según:

6

Y i es la varianza muestral de Gj’ estimada mediante i = V/nj, siendo V la varianza regional esperada de los puntos G´ que, asumiendo distribución uniforme, es igual a 1/12.

R se distribuye según con (N-1) grados de libertad, siendo N el número de estaciones de la región. Esto fue confirmado por los autores con experimentos numéricos mediante simulaciones de Montecarlo. Una vez obtenido R, si excede el valor de (1-), se rechaza la hipótesis de homogeneidad con un grado de significancia . El test requiere el conocimiento previo de la función de distribución de la población.

CHOCO

RISARALDA

TOLIMA

QUINDIO

CAUCA

VALLE DELCAUCA

N

OCEANOPACIFICO

7

Figura 1. Localización de las estaciones Figura 2. Coeficiente de correlación promedio entre grupos vs número de clusters.

Análisis Discriminante. Este método permite asignar una estación a un grupo definido a priori en función de una serie de características del mismo. La base de dicho análisis consiste en establecer una función discriminante que permita clasificar las variables en los diferentes grupos. Hay tantas funciones discriminantes como grupos menos uno (k – 1) y para que sean óptimas han de proporcionar una regla de clasificación que minimice la probabilidad de cometer errores. Obtenidas las cargas discriminantes, se obtiene una clasificación de las variables basada en el teorema de Bayes, y la probabilidad que una estación con una puntuación discriminante determinada pertenezca a uno u otro grupo se estima a través de:

Siendo P (Gi) la probabilidad previa de que una estación pertenezca a un grupo determinado de la muestra, P(D/Gi) la probabilidad condicional de obtener determinada puntuación discriminante bajo el supuesto que la misma pertenezca a otro grupo, P(Gi/D) es la probabilidad posterior, que se calcula con el teorema de Bayes, permitiendo asignar a cada sujeto al grupo en el cual su probabilidad posterior es mayor. La discriminación entre los k grupos se realiza mediante el cálculo de las funciones discriminantes. Existen varios procedimientos, en este caso se utilizó el de Fisher por ser uno de los más utilizados. Dicho análisis se realizó a partir de la clasificación obtenida en el cluster jerárquico, y fue aplicando a las 10 primeras componentes principales. El análisis de Componentes Principales (ACP), es una técnica multivariada que permite transformar un conjunto de variables correlacionadas en un nuevo conjunto menor de variables no correlacionadas (ortogonales). El método intenta identificar la dimensión del campo espacial medido con las estaciones de precipitación. (Johnson, 2000). En esencia, El ACP extrae p raíces o autovalores, y p autovectores de la matriz de correlación. El número de raíces corresponde al rango de la matriz, que es igual al número de vectores linealmente independientes. Los autovalores son numéricamente iguales a la suma de los cuadrados de los pesos factoriales y representan la relativa proporción de la varianza que representa cada componente. (Jhonson, 2000), trata la metodología inherente a este análisis. El ACP no requiere una determinada distribución de probabilidad en los datos, aunque los mejores resultados se pueden obtener cuando los datos originales son normales multivariados. A partir de las 10 primeros CP, que representan el (72%) de la variabilidad del conjunto de datos de precipitación, se efectuó el análisis Discrimiante, a partir de los resultados obtenidos en el cluster jerárquico.

3. ANALISIS Y DISCUSION DE RESULTADOS

3.1 ANALISIS DE CLUSTER JERARQUICO

La figura 2 presenta los coeficientes de correlación promedio por grupos, para diferentes clusters. Teóricamente, el número de grupos a emplear se define, cuando se presenta un cambio significativo en la media del coeficiente de correlación intergrupos. En este caso se tomaron 3 grupos de estaciones de precipitación. ARIDE (2001).

La figura 3 presenta los resultados del test de Dalrymple (1960) para el grupo 3. Se observa que todas las estaciones pasaron dicho test. Este método tienen la desventaja de tener que asumir una determinada función de distribución y la posibilidad de encontrar heterogeneidad en períodos de retorno distintos al utilizado en la prueba. Hosking (1987), plantea que tiene un escaso poder estadístico, porque en la mayoría de los casos confirma la homogeneidad regional. Las aplicaciones del test se asocian casi siempre a un método de regionalización del

8

tipo variable índice, pero la escala del método, de comparar el ajuste regional con los límites de confianza del ajuste local, es utilizable con cualquier método de regionalización.

Figura 3. Resultados del test de Dalrymple para el grupo 1 de estaciones

Método de Wiltshire y Berán (1987b) La tabla 1 resume los resultados del test aplicado a los grupos, la prueba fue aceptada para los tres grupos con un 95% de confiabilidad, debido a que los valores de G obtenidos, son menores que la evaluación de la correspondiente prueba de . Las simulaciones auxiliares de Montecarlo llevadas a cabo por Wiltshire muestran que R efectivamente se distribuye según una , aunque el poder estadístico del test es solo moderado. Este test fue empleado también por FREND (1989), presentando como inconveniente la necesidad de estimar previamente la ley regional F(x) para realizar el cálculo de los valores de Gij y como ventaja la posibilidad de aplicación a cualquier tipo de regionalización. Para cada una de las regiones se emplearon los parámetros de la función de distribución EV1.

Tabla 1. Test de Wiltshire y Berán (1987b) para los tres grupos homogéneos seleccionados

9

ESTACION nj Vj nj*Vj uj 1/uj g" gj/uj (gj-g")2/uj R X2

ACTO TULUA 27 0.00015 0.0039 0.0031 324.00 0.48 156.26 0.10BUGALAGRANDE 27 0.00012 0.0033 0.0031 324.00 0.45 146.22 0.77CAÑAVERALEJO 27 0.00012 0.0033 0.0031 324.00 0.45 144.97 0.90EL PALACIO 27 0.00011 0.0031 0.0031 324.00 0.49 157.68 0.06EL TOPACIO 27 0.00011 0.0029 0.0031 324.00 0.48 156.43 0.10GALICIA 27 0.00011 0.0030 0.0031 324.00 0.49 157.29 0.07GARZONERO 27 0.00011 0.0028 0.0031 324.00 0.51 164.36 0.02LA ARGENTINA 27 0.00013 0.0036 0.0031 324.00 0.48 154.71 0.16LA BALSA 27 0.00010 0.0027 0.0031 324.00 0.51 165.22 0.03LA FONDA 27 0.00011 0.0028 0.0031 324.00 0.47 151.73 0.33LA HERRADURA 27 0.00014 0.0039 0.0031 324.00 0.39 127.65 3.64LOS CRISTALES 27 0.00009 0.0025 0.0031 324.00 0.50 161.82 0.00R. CALI 27 0.00010 0.0026 0.0031 324.00 0.52 167.38 0.09SAN ANTONIO 27 0.00010 0.0027 0.0031 324.00 0.53 172.24 0.32SAN PABLO 27 0.00013 0.0036 0.0031 324.00 0.46 149.36 0.49SANTA INÉS 27 0.00009 0.0025 0.0031 324.00 0.51 166.69 0.07VIJES 27 0.00010 0.0028 0.0031 324.00 0.52 168.93 0.15VILLACOLOMBIA 27 0.00008 0.0022 0.0031 324.00 0.52 167.76 0.10VILLAMARÍA 27 0.00012 0.0032 0.0031 324.00 0.47 151.61 0.33VILLARICA 27 0.00011 0.0029 0.0031 324.00 0.50 161.26 0.00

0.00223 0.0603 0.49 3149.56 7.73 7.73 30.10ALCALA 27 0.00011 0.0029 0.0031 324.00 0.49 157.61 0.06AUSTRIA 27 0.00010 0.0028 0.0031 324.00 0.49 159.85 0.01CORINTO 27 0.00011 0.0028 0.0031 324.00 0.51 166.10 0.05EL CASTILLO 27 0.00012 0.0032 0.0031 324.00 0.49 157.52 0.06EL TRAPICHE 27 0.00013 0.0036 0.0031 324.00 0.49 157.48 0.06GUACARI 27 0.00014 0.0037 0.0031 324.00 0.42 135.59 2.15ICA 27 0.00013 0.0035 0.0031 324.00 0.50 163.52 0.01IRLANDA 27 0.00010 0.0028 0.0031 324.00 0.52 168.13 0.12LA DIANA 27 0.00013 0.0035 0.0031 324.00 0.51 163.94 0.01LA FLORIDA 27 0.00011 0.0028 0.0031 324.00 0.52 167.70 0.10LA GITANA 27 0.00012 0.0032 0.0031 324.00 0.50 161.79 0.00LA MAGDALENA 27 0.00009 0.0025 0.0031 324.00 0.55 178.39 0.83LA QUINTA 27 0.00012 0.0033 0.0031 324.00 0.52 168.21 0.12LA SELVA 27 0.00008 0.0021 0.0031 324.00 0.53 172.56 0.34LA SOLEDAD 27 0.00014 0.0037 0.0031 324.00 0.46 149.32 0.50LOS ALPES 27 0.00013 0.0034 0.0031 324.00 0.46 149.58 0.48MANUELITA 27 0.00010 0.0026 0.0031 324.00 0.54 175.73 0.58MONTELORO 27 0.00013 0.0036 0.0031 324.00 0.48 154.31 0.18PARDO 27 0.00011 0.0029 0.0031 324.00 0.50 162.63 0.00PICHICHÍ 27 0.00015 0.0040 0.0031 324.00 0.49 160.31 0.01SILVIA 27 0.00013 0.0034 0.0031 324.00 0.51 165.25 0.03SUMATORIAS 0.00246 0.0664 0.50 3401.25 5.71 5.71 28.40LA VICTORIA 27 0.00014 0.0037 0.0031 324.00 0.47 152.82 0.26MIRAVALLES 27 0.00009 0.0024 0.0031 324.00 0.56 180.71 1.08PTO MOLINA 27 0.00009 0.0024 0.0031 324.00 0.55 179.65 0.96SABANAZO 27 0.00010 0.0027 0.0031 324.00 0.49 157.24 0.07ZARAGOSA 27 0.00015 0.0041 0.0031 324.00 0.41 132.35 2.71

0.00056 0.0153 0.02 0.50 802.76 5.08 5.08 9.49

Análisis Discriminante a las Componentes principales. Los resultados se resumen en la tabla 2 en la segunda columna se observa el grupo real clasificado, y en la tercera, se aplicó la metodología basada en la teoría de Bayes y la probabilidad que un sujeto con una puntuación discriminante determinada pertenezca a uno u otro grupo. El resultado indica que sólo 1 una estación no está correctamente clasificada (Corinto). La correlación canónica es una medida de asociación entre las puntuaciones discriminantes y los grupos. Una buena función discriminante es aquella que proporciona 2 o más grupos con puntuaciones discriminantes medias muy diferentes entre si y en cambio con poca variabilidad interna dentro de cada grupo. Una forma de determinar la contribución de cada variable a la función discriminante consiste en examinar la correlación entre las variables de la función y los de cada una de las variables independientes.

La distancia de Mahalanobis es una generalización de la distancia euclídea que tiene en cuenta la matriz de covarianzas intragrupos. La aplicación de éste criterio consiste en asignar cada individuo al grupo para el cual la distancia de Mahalanobis sea mínima. Su expresión es:

Donde Xia es la media de la variable i en el grupo a.

Las tablas 3 y 4 resumen las funciones canónicas discriminantes. Los valores de 1 = 0.04 y de la correlación canónica (0.929) obtenidos para las dos primeras funciones discriminantes, indican que la función obtenida es significativa y su poder discriminante alto.

Tabla 2. Análisis discriminante de los grupos homogéneos seleccionados

10

Grupo Grupo No Estación real pronost. DM DM

P(G=g | D=d) Grupo P(G=g | D=d) F1 F2p gl

1 ACTO TULUA 1 1 0.57 2 1.00 1.13 2 0.00 18.47 0.88 -2.312 ALCALA 2 2 0.11 2 0.95 4.46 1 0.05 10.56 -0.28 1.133 AUSTRIA 2 2 0.72 2 1.00 0.66 1 0.00 26.59 -3.13 0.534 BUGALAGRANDE 1 1 0.33 2 1.00 2.24 3 0.00 18.86 2.54 -0.365 CAÑAVERALEJO 1 1 0.48 2 1.00 1.45 2 0.00 30.11 2.18 -2.586 CORINTO 2 1 0.10 2 0.60 4.55 2 0.40 5.36 -0.22 -0.417 EL CASTILLO 2 2 0.13 2 1.00 4.02 1 0.00 41.29 -3.90 1.808 EL PALACIO 1 1 0.99 2 1.00 0.02 2 0.00 21.06 1.74 -1.579 EL TOPACIO 1 1 0.36 2 1.00 2.06 2 0.00 21.80 0.93 -2.79

10 EL TRAPICHE 2 2 0.64 2 1.00 0.90 1 0.00 17.00 -1.55 1.1311 GALICIA 1 1 0.40 2 0.98 1.83 2 0.02 9.65 0.51 -0.7312 GARZONERO 1 1 0.15 2 0.93 3.84 2 0.07 9.03 0.66 0.2013 GUACARI 2 2 0.14 2 0.75 3.95 1 0.25 6.18 -0.71 -0.6014 ICA 2 2 0.79 2 1.00 0.47 1 0.00 14.69 -1.91 0.0115 IRLANDA 2 2 0.52 2 0.99 1.33 1 0.01 10.88 -1.37 -0.0816 LA ARGEN 1 1 0.28 2 0.97 2.51 2 0.03 9.60 0.02 -1.4817 LA BALSA 1 1 0.19 2 1.00 3.31 3 0.00 21.10 3.34 -0.9918 LA DIANA 2 2 0.91 2 1.00 0.18 1 0.00 19.01 -2.43 0.1519 LA FLORIDA 2 2 1.00 2 1.00 0.01 1 0.00 20.59 -2.40 0.6120 LA FONDA 1 1 0.85 2 1.00 0.33 2 0.00 21.07 1.97 -1.0821 LA GITAN 2 2 0.70 2 1.00 0.72 1 0.00 26.20 -2.63 1.3522 LA HERRA 1 1 0.40 2 1.00 1.83 3 0.00 20.16 2.49 -0.5023 LA MAGDA 2 2 0.46 2 0.99 1.56 1 0.01 10.81 -1.47 -0.3624 LA QUINTA 2 2 0.73 2 1.00 0.62 1 0.00 27.29 -2.96 1.0225 LA SELVA 2 2 0.80 2 1.00 0.46 1 0.00 22.96 -2.88 0.1826 LA SOLEDAD 2 2 0.24 2 1.00 2.87 1 0.00 36.99 -3.52 1.7527 LA VICTORIA 3 3 0.08 2 1.00 5.08 1 0.00 64.58 6.33 4.9728 LOS ALPES 2 2 0.52 2 1.00 1.32 1 0.00 31.16 -3.25 1.2329 LOS CRISTALES 1 1 0.26 2 1.00 2.69 2 0.00 36.10 2.70 -2.7530 MANUELITA 2 2 0.88 2 1.00 0.26 1 0.00 22.72 -2.40 1.0731 MIRAVALLES 3 3 0.14 2 1.00 3.98 1 0.00 16.90 4.48 1.4132 MONTELORO 2 2 0.92 2 1.00 0.17 1 0.00 21.91 -2.36 0.9733 PARDO 2 2 0.37 2 1.00 2.00 1 0.00 15.04 -2.22 -0.8534 PICHICHÍ 2 2 0.68 2 1.00 0.76 1 0.00 18.92 -2.57 -0.2835 PIENDAMO 2 2 0.52 2 1.00 1.29 1 0.00 23.10 -2.00 1.6636 PTO FRAZ 2 2 0.52 2 1.00 1.30 1 0.00 22.04 -2.95 -0.3837 PTO MOLI 3 3 0.58 2 1.00 1.08 1 0.00 44.59 4.63 4.4338 R. CALI 1 1 0.31 2 1.00 2.32 2 0.00 33.91 2.44 -2.8039 SABANAZO 3 3 0.33 2 1.00 2.23 1 0.00 53.24 5.27 4.7840 SAN ANTO 1 1 1.00 2 1.00 0.01 2 0.00 19.20 1.57 -1.4641 SAN EMIG 2 2 0.64 2 1.00 0.90 1 0.00 23.30 -3.01 -0.0942 SAN PABL 1 1 0.94 2 1.00 0.13 2 0.00 22.99 1.90 -1.7243 SANTA IN 1 1 0.11 2 0.99 4.40 2 0.01 14.44 -0.20 -2.5944 SILVIA 2 2 0.18 2 1.00 3.41 1 0.00 38.43 -3.53 1.9645 VIJES 1 1 0.91 2 1.00 0.19 2 0.00 16.85 1.17 -1.6046 VILLACOL 1 1 0.83 2 1.00 0.37 2 0.00 17.06 1.06 -1.8147 VILLAMAR 1 1 0.61 2 1.00 0.98 3 0.00 26.74 2.57 -1.3148 VILLARIC 1 1 0.45 2 1.00 1.61 2 0.00 15.76 1.57 -0.2649 ZARAGOSA 3 3 0.02 2 0.79 7.40 1 0.21 10.07 2.91 1.37

GRUPO MAYOR

P(D>d | G=g)

F discriminanteSEGUNDO GRUPO MAYOR

La de Wilks permite evaluar la información que aporta cada función discriminante en particular. También se observa que los valores de la correlación canónica decrecen, y la primera función discrimina más que la segunda. La correlación canónica mide la desviación de las puntuaciones discriminantes entre grupos respecto a las desviaciones totales sin distinguir grupos. El autovalor mide la desviación de las puntuaciones discriminantes entre los grupos respecto a las de dentro de los grupos. En ambos casos si la desviación es grande, la dispersión será debida a la diferencia entre grupos y en consecuencia la función discriminará mucho los grupos.

Tabla 3. Resultados del test de Wilks para las funciones canónicas

Contraste de las funciones

de Wilks Chi-cuadrado Gl Sig.

1 a la 2 .040 133.856 20 .0002 .292 51.106 9 .000

Tabla 4. Autovalores de las funciones canónicas discriminantes.

Función Autovalor % de varianza % acumulado Correlación canónica

1 6.345 72.3 72.3 .9292 2.426 27.7 100.0 .842

a Se han empleado las 2 primeras funciones discriminantes canónicas en el análisis.

4. CONCLUSIONES Y RECOMENDACIONES

11

La homogeneización de las series para el tratamiento conjunto de los datos, permite, hacer análisis más robustos, y reducir la incertidumbre existente respecto a la representatividad y consistencia de una muestra local. Así mismo, una excesiva heterogeneidad de los datos en la región puede conducir a valores erróneos en la estimación de parámetros estadísticos. Aunque no existe un procedimiento que asegure la correcta definición de la región para el análisis de precipitación o caudal, lo recomendable es emplear el método geográfico y confirmarlo con un test de homogeneidad, que verifique la región.

El método geográfico puede considerarse el más adecuado para definir las regiones, cuya homogeneidad debe ser contrastada con un test estadístico. La selección del método de comprobación depende del grado de homogeneidad que se quiera asumir. A nivel de conclusión, el método de Dalrymple es de poca potencia, al no considerar la homogeneidad de cuantiles diferentes a un Tr = 10. El test de Wiltshire, y en general los test basados en la prueba estadística de tienen una potencia moderada.

Gran parte de los métodos de regionalización desarrollados en Colombia, parten de la regionalización en función de un conjunto de características específicas de las cuencas, dicha clasificación rara vez se confirma al comparar los estadísticos observados, por lo cual es recomendable explorar otras técnicas complementarias en los métodos de regionalización o definición de series homogéneas. El test de homogeneidad regional es necesario para probar que una muestra de observaciones de un fenómeno hidrológico es homogénea, es decir, para cuantificar los límites de las variaciones admisibles, fuera de los cuales se rechaza la hipótesis de homogeneidad; definiendo la región de aceptación de la hipótesis, podrían considerarse como homogéneas, las muestras que quedan dentro de esas bandas.

Vale la pena resaltar que si las series presentan inconsistencias, al hacer la clasificación estadística, se obtienen heterogeneidades e inconsistencias geográficas. Estas situaciones conducen a que una prueba de homogeneidad sea rechazada, por lo cual se recomienda efectuar un tratamiento previo exhaustivo de la información antes de llevar a cabo el análisis de regionalización. Puede ocurrir también que la heterogeneidad sea debida a eventos extremos muy localizados, lo cual conduce a asumir (al utilizar dichos datos) que estos sucesos se producen en toda la región.

REFERENCIAS BIBLIOGRAFICAS

Acreman M.C. y Sincalir C. D., 1986: “Classification of Drainage basins according to their physical characteristics ; An application for flood frecuency analysis in Scotland” J. Hydrol., 84 365-380.

Arias A,, Y. y Soto, C., 2000 “Regionalización de Caudales Medios de las Corrientes Afluentes Superficiales al Río Cauca entre Salvajina y Cartago”, Trabajo de Grado, Universidad del Valle - Universidad Nacional de Colombia, Santiago de Cali, Palmira – Colombia.

ARIDE, 2001. Assesment of the Regional Impact of Droughts in Europe. Final Report. Institute of Freiburg. Freiburg.Germany.

Benson M.A., 1962: “Evaluation of methods for evaluating the ocurrence of floods “ Water Resour. Res., 4 (5), 891-895.

Dalrymple, T., 1960: Flood Frecuency analyses” Water Supply Pap. 1543-A, U.S. Geological Survey, Reston, Va.

De Coursey D. G., 1973: “ Objetive regionalizaton of peak flows rates”. Floods and Droughts, 395-405, Ed. E.F. Koelzer, V.A. Koelzer y K. Mahmood. Proc of the second International Symposium in Hydrology, Sept. 1972, fot Collins, Colorado USA.

12

Erazo, A. M. “Estudio de Regionalización de Caudales Máximos para Diseño" Corporación Autónoma Regional del Valle del Cauca. 1998.

Ferrer, J, P. 1996. Función de distribución SQRT-Et max en el análisis regional de máximos hidrológicos. Aplicación a lluvias diarias. Tesis Doctoral. Dpto. Ingeniería Civil Hidráulica y Energética. Universidad Politécnica de Madrid.

FREND. 1989: Flow Regimes from experimental and network data, Vol, 1 Hydrologycal studies”. Ed. Institute of Hydrology, Wallinford. 344 pp.

HIMAT, IDEAM e Ingeniería y Recursos Hídricos Ltda. 1995. “Regionalización de Crecientes Máximas”, Santa Fé de Bogotá D.C. 1995.

Hosking J.R.M., 1987: “ Regional homogeneity: Review of statistical flood frecuency estiamtion”. Open file report n 6, Institute of Hydrology, 34 pp.

Instituto del Agua., 1992 “Estudio hidrológico de ramblas Costeras de la región de Murcia”. Univ Murcia.

Johnson, Dallas. 2000. Applied multivariate methods for data analysis. International Thompson Plublishing.

Lettenmaier D.P. y Potter K.W., 1985: “Testing flood frecuency estimation methods using a regional flood generating modelo”. Water Resour. Res,. 21(12), 1903 -1914

MEJIA M., PERRY. 1987. Estudio de aguas en el área geográfica del Valle del Cauca bajo la jurisdicción de la CVC. Colombia.

Mesa, O. Et al. 1998. Introducción al clima de Colombia. Universidad Nacional de Colombia. Sede Medellín. Facultad de Minas. Posgrado de Aprovechamientos Hidráulicos. Medellín - Colombia.

Mosley M.P., 1 981:”Delimitation of New Zealand into hydrologic regions”. J. Hydrol., 49, 173-192.

NERC, 1975: “Flood studies report” Nat Environ. Res. Council, London, vols. 1 – 5, 1100 pp.

Regalado H., G. Et al 1984. “Estudio Regional de Frecuencias de Caudales Máximos para la Cuenca del Pacifico”, VI Seminario Nacional de Hidráulica. Santiago de Cali.

Wiltshire S., 1986: Identification of homogeneous regions for flood frecuency analysis” J. Hydrol., 84, 287 – 302.

Wiltshire S. Y Beran M., 1987a: “Multivariates Techniques for the identification of Homogeneous flood frecuency Regions”. Regional Flood Frecuency Analysis, 133-145, Ed V.P. Singh. Reidel Publising Company

Wiltshire S. Y Beran M., 1987b: “A significance test for homogeneity of flood frecuency regions”. Regional Flood Frecuency analysis, 147-158, Ed V.P. Singh. Reidel Publising Company.

13